引言

本节将介绍关于凸集的基本信息，包括概念、基本性质以及常见凸集。

凸优化问题与凸集合凸函数的关系

在最优化问题范畴中，凸优化问题是一类常见的、并且性质优秀的优化问题。一些情况下可以通过凸优化问题来解决非凸优化问题。

而凸集合与凸函数决定了该优化问题是凸优化问题。具体表现在：
在最优化问题概述中我们介绍了可行域的概念。它可能并不仅仅被定义域空间描述，并且也可能伴随着约束条件的限制。在这里为了简化问题，仅观察定义域空间的描述。

• 目标函数$f(x)$是一个凸函数；
• 而$x$的可行域$\mathcal{S}\Rightarrow x\in \mathcal{S}$是一个凸集合。

$$\{\begin{array}{l}\min f(x)\\ \text{s.t. }x\in \mathcal{S}\end{array}$$

凸优化问题简单示例

这里通过两个简单示例描述凸优化相关的优秀性质：

• 关于一元函数$\mathcal{G}(x)$的最小化问题数学符号表示如下：
  $$\{\begin{array}{l}\min \mathcal{G}(x)\\ \text{s.t. }x\in [a,b)\end{array}$$
• 假设关于$\mathcal{G}(x)$的函数图像表示如下：
  

观察左侧函数图像，在$[a,b)$区间内，可以找到该函数的最小点，并且该点是一个平稳点——在该点处函数的导数为$0$；

同时观察右侧函数图像，同样可以找到该函数的最小点。只不过区别于左侧函数图像的是：该区间内函数的平稳点存在若干个：

• 观察第一、第三个红色点，它们都是其各自邻域内的最小值，也称作局部最优解；其中第一个红色点不仅是局部最优解，而且是$[a,b)$范围内的全局最优解。
  但这些红色点也同样都是平稳点,也就是说：仅通过平稳点无法确定其是否为全局最优解。
• 再回顾左侧函数图像：它的局部最优解就是全局最优解，并且平稳点对应的解就是全局最优解。
  这是凸函数的重要性质;相反地，右侧图像描述的函数被称作非凸函数。

凸集的简单示例

已知函数：$\mathcal{G}(x_1,x_2)=x_1^2+x_2^2$，想要求解在可行域$\mathcal{S}$内关于$\mathcal{G}(x_1,x_2)$的最小值。对应优化问题表示如下：
$$\{\begin{array}{l}\min \mathcal{G}(x_1,x_2)=x_1^2+x_2^2\\ \text{s.t. }(x_1,x_2)\in \mathcal{S}\end{array}$$
现在存在两个可行域${\mathcal{S}}_1,{\mathcal{S}}_2$，对应图像表示如下：

从几何角度观察，函数$\mathcal{G}(x_1,x_2)$描述的图像形状是圆，上述图像中的虚线表示函数图像可能出现的等值线。

• 观察左侧图像，在可行域${\mathcal{S}}_1$范围内取到合适的$x^{\ast }(x_1^{\ast },x_2^{\ast })$，使得$\mathcal{G}(x_1^{\ast },x_2^{\ast })$达到最小，很明显，是上述的红色点。作为最优解的$x^{\ast }$，可以发现：$x^{\ast }$点所在位置是函数$\mathcal{G}(x_1,x_2)$与可行域${\mathcal{S}}_1$描述范围的切点；也就是说：$x^{\ast }$点处的负梯度方向$-\nabla \mathcal{G}(x_1^{\ast },x_2^{\ast })$与切线方向垂直。
  其中红色箭头表示负梯度方向。关于负梯度方向，详见线搜索方法(方向角度)。

  这意味着：从可行域${\mathcal{S}}_1$范围内任取一点$x$，那么向量$x-x^{\ast }$与负梯度方向之间的夹角总是$\ge 90^o$。如果用向量内积的形式表示，必然有：
  这里的$\mathcal{G}(x^{\ast })$表示$\nabla \mathcal{G}(x_1^{\ast },x_2^{\ast })$,后续同理。
  $$-[\nabla \mathcal{G}(x^{\ast }){]}^T(x-x^{\ast })\le 0\forall x\in {\mathcal{S}}_1$$
  最终归纳得到如下等价条件：
  $$x^{\ast }\text{ is Optimal }\iff -[\nabla \mathcal{G}(x^{\ast }){]}^T(x-x^{\ast })\le 0\forall x\in {\mathcal{S}}_1$$

• 观察右侧图像，可以按照上述寻找切点的方式去寻找最优解。假设找到了右侧的红色点。但这个最优解并不满足上述的等价条件。
  见下图中右侧两个红色箭头明显是一个锐角。
  

综上，可行域内任意一点$x$与最优解$x^{\ast }$之间满足如上等价条件，那么该可行域是凸集；反之为非凸集。从而将可行域${\mathcal{S}}_1$称为凸集；而可行域${\mathcal{S}}_2$称作非凸集。相反，如果一个可行域被确定是凸集，那么它同样存在一些优秀性质：

• 在凸集中根据上述等价条件找到的最优解一定是全局最优解；
• 通过求解导数/梯度获取的平稳定一定是最值点。

基本定义：凸集

关于凸集$(\text{Convex Set})$的定义表示如下：
$$\forall x,y\in \mathcal{C};\forall \lambda \in [0,1]\Rightarrow \lambda \cdot x+(1-\lambda )\cdot y\in \mathcal{C}$$
文字的描述可简单表述为：可行域$\mathcal{C}$中任意两点间的连线，其连线上的任一点仍属于该可行域$\mathcal{C}$。示例图像表示如下：

• 第二张图也被称作多面体。
• 很明显，最后一个图描述的可行域不是凸集，其连线上的点并不全在可行域上。
  

关于凸集性质的等价条件，凸组合，凸包

关于凸集合性质存在如下等价条件：如果某可行域$\mathcal{C}$是一个凸集，对于$\forall x_1,x_2,\cdots ,x_k\in \mathcal{C}$，且对于$\forall {\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_k\ge 0$且$\begin{array}{r}\sum _{i=1}^k{\lambda }_i=1\end{array}$，必然有：
反之同样可以推出$\mathcal{C}$是一个凸集。
$$\sum _{i=1}^k{\lambda }_i\cdot x_i\in \mathcal{C}$$
这里以$k=3$为例。对于$x_1,x_2,x_3\in \mathcal{C},\forall {\lambda }_1,{\lambda }_2,{\lambda }_3\ge 0$且${\lambda }_1+{\lambda }_2+{\lambda }_3=1$，对应${\lambda }_1{x}_1+{\lambda }_2{x}_2+{\lambda }_3{x}_3$在可行域$\mathcal{C}$中的描述表示为：$x_1,x_2,x_3$围成的三角形的范围：
显然，该三角形围成的范围是可行域$\mathcal{C}$的一部分。

对于表达式$\begin{array}{r}\sum _{i=1}^k{\lambda }_i\cdot x_i\end{array}$，它称作$x_1,x_2,\cdots ,x_k$的凸组合$(\text{Convex Combination})$。
条件不能漏掉~${\lambda }_i(i=1,2,\cdots ,k)\ge 0$且${\sum }_{i=1}^k{\lambda }_i=1$。

相应的组合概念如：
很明显，从关于${\lambda }_i(i=1,2,\cdots ,k)$的约束程度角度，有：凸组合 $>$ 仿射组合；非负组合 $>$ 线性组合。

• 线性组合$(\text{Linear Combination})$：${\sum }_{i=1}^k{\lambda }_i\cdot x_i$，虽然与凸组合共用相同的表达式，但其对${\lambda }_i(i=1,2,\cdots ,k)\in \mathbb{R}$即可，没有过多的约束；
• 仿射组合$(\text{Affine Combination})$：依然是上述表达式，但相比于凸组合，只要求${\sum }_{i=1}^k{\lambda }_i=1$，没有符号要求。
• 非负组合$(\text{Nonnegative Combination})$：依然是上述表达式，但相比于凸组合，仅要求${\lambda }_i(i=1,2,\cdots ,k)\ge 0$，没有加和为$1$的要求。

关于凸包$(\text{Convex Hull})$，它针对的是任意一个集合，并非只有凸集。在选定集合$\mathcal{C}$的条件下，从$\mathcal{C}$中取点后作凸组合，将所有凸组合结果构成一个新集合，该集合被称作凸包。

凸包的作用：由于凸包是由凸组合构成的集合，因而：对于任意集合$\mathcal{C}$(凸、非凸)，它的凸包一定是凸集合。从而凸包是优化过程中将非凸集合凸化的一个工具。
这里作为科普，不做过多描述~

常见凸集

常见的凸集合有：

• 超平面$(\text{Hyperplane})$，其表达式表示如下：
  H = { x ∣ a T x = b } ( a ≠ 0 ) \mathcal H = \{x \mid a^T x = b\}(a \neq 0) H={x∣aTx=b}(a=0)
• 半空间$(\text{Halfspace})$，其表达式表示为：
  { H + = { x ∣ a T x ≥ b } ( a ≠ 0 ) H − = { x ∣ x T x ≤ b } ( a ≠ 0 ) \begin{cases} \mathcal H^{+} = \{x \mid a^Tx \geq b \}(a \neq 0) \\ \mathcal H^{-} = \{x \mid x^Tx \leq b\}(a \neq 0) \end{cases} {H+={x∣aTx≥b}(a=0)H−={x∣xTx≤b}(a=0)​
  对应图像描述表示为：
  
• 多面体$(\text{Polyhedra})$：由多个线性不等式刻画的集合。对应表达式表示如下：
  由于一个线性不等式刻画的是半空间,那么由多个线性不等式对应半空间的交集/围成的空间就是多面体。
  { x ∣ a i T x ≤ b i , i = 1 , 2 , ⋯   , M } \{x \mid a_i^T x \leq b_i,i=1,2,\cdots,\mathcal M\} {x∣aiT​x≤bi​,i=1,2,⋯,M}
  关于多面体集合$\mathcal{P}$的图像示例描述表示为：
  
  上面关于多面体的定义是关于线性不等式所刻画的集合；相反，线性等式刻画的集合是多面体吗$?$自然也是。因为可以将线性等式$a_i^{T}x=b_i$刻画为如下两个线性不等式的交集：
  从而又将线性等式刻画的集合转化为线性不等式刻画的集合。
  $$a_i^{T}x=b_i\iff \{\begin{array}{l}{a}_i^{T}x\le b_i\\ -a_i^{T}x\le -b_i\end{array}i=1,2,\cdots ,\mathcal{M}$$
• 欧几里得球$(\text{Euclidean Balls})$：如果球的中心$x_c$和半径$r$已知，对应表达式表示如下：
  这里的$||u|{|}_2\le 1$描述的是中心为$0$，半径为$1$的单位球空间。对应的$r\cdot u$则表示对球空间进行放缩;$x_c+r\cdot u$则是对放缩后的结果进行平移~
  B ( x c , r ) = { x ∣ ∥ x − x c ∥ 2 ≤ r } = { x c + r ⋅ u ∣ ∥ u ∥ 2 ≤ 1 } \begin{aligned} \mathcal B(x_{c},r) & = \{x \mid \| x - x_c\|_2 \leq r\} \\ & = \{x_c + r \cdot u \mid \|u\|_2 \leq 1\} \end{aligned} B(xc​,r)​={x∣∥x−xc​∥2​≤r}={xc​+r⋅u∣∥u∥2​≤1}​
  这仅仅是二范数的结果，调整范数，可以得到范数球$(\text{Norm Balls})$。
  相关文章见下方链接~
• 椭球$(\text{Ellipsoid})$：若椭球中心$x_c$已知，对应表达式表示如下：
  其中矩阵$\mathcal{P}$是正定矩阵，否则${\mathcal{P}}^{-1}$无法求解。
  { x ∣ ( x − x c ) T P − 1 ( x − x c ) ≤ 1 } \{x \mid (x -x_c)^T \mathcal P^{-1} (x - x_c) \leq 1\} {x∣(x−xc​)TP−1(x−xc​)≤1}
  为什么是${\mathcal{P}}^{-1}$，它有什么作用$?$这里假设正定矩阵$\mathcal{P}$与对应${\mathcal{P}}^{-1}$表示如下：
  $$\mathcal{P}=\left(\begin{array}{c}20\\ 04\end{array}\right)\Rightarrow {\mathcal{P}}^{-1}=\left(\begin{array}{c}\begin{array}{r}\frac{1}{2}0\\ 0\frac{1}{4}\end{array}\end{array}\right)$$
  将${\mathcal{P}}^{-1}$带入到原式，有：
  $$(x-x_c{)}^T\left(\begin{array}{c}1/20\\ 01/4\end{array}\right)(x-x_c)\le 1$$
  从而有：
  $$\frac{(x_1-x_{c_1}{)}^2}{2}+\frac{(x_2-x_{c_2}{)}^2}{4}\le 1$$
  上式中描述的椭球空间，其长轴、短轴的半轴长分别是$\sqrt{2},\sqrt{4}$，这恰好是正定矩阵$\mathcal{P}$特征值的开平方。因此${\mathcal{P}}^{-1}$本质上描述$\mathcal{P}$与椭球长短轴之间的关联关系。
• 二阶锥$(\text{Second-Order Cone})$
  关于锥集合$\mathcal{C}$的定义可描述为：
  $$\text{if }x\in \mathcal{C}\Rightarrow \lambda \cdot x\in \mathcal{C}\forall \lambda \ge 0$$
  而二阶锥的定义可表示为：
  假设在$n+1$维的特征空间中，其中$x=(x_1,x_2,\cdots ,x_n{)}^T\in {\mathbb{R}}^n$,最后一维特征表示为$t$。下面公式则表示为:前$n$维的二范数结果$||x|{|}_2\le$第$n+1$维的特征结果$t$。
  $$\{(x,t)\mid \Vert x{\Vert }_2\le t\}$$
  例如：$x$是一个二维向量，那么上式的表达有：
  $$\sqrt{x_1^2+x_2^2}\le t$$
  简单绘制一下它的图像：

import numpy as np
import matplotlib.pyplot as plt
import math 

x = np.linspace(-5,5,50)
y = np.linspace(-5,5,50)
t = 5.0

def f(x,y):
    return math.sqrt((x ** 2) + (y ** 2))

ax = plt.axes(projection='3d')

for i in list(x):
    for j in list(y):
        if f(i,j) <= t:
            ax.scatter(i,j,f(i,j),c="tab:blue",s=2)
        else:
            continue
plt.show()

最终结果表示如下：

• 半定矩阵锥：

  • 首先，划定一个集合${\mathcal{S}}^n$，它描述：所有$n$阶对称矩阵组成的集合；
    可见，集合中的每个元素都是$n$阶对称矩阵。
  • 在集合${\mathcal{S}}^n$的基础上，划定一个集合${\mathcal{S}}_{+}^n$，它描述：所有$n$阶半正定矩阵组成的集合，记作 S + n = { X ∈ S n ∣ X ≽ 0 } \mathcal S_{+}^n = \{\mathcal X \in \mathcal S^n \mid \mathcal X \succcurlyeq 0\} S+n​={X∈Sn∣X≽0}
    其中$\mathcal{X}\succcurlyeq 0\iff {\mathcal{Z}}^T\mathcal{XZ}\ge 0\forall \mathcal{Z}$。
  • 同样在集合${\mathcal{S}}^n$的基础上，划定一个集合${\mathcal{S}}_{++}^n$，它描述：所有$n$阶正定矩阵组成的集合，记作 S + + n = { X ∈ S n ∣ X ≻ 0 } \mathcal S_{++}^n = \{\mathcal X \in \mathcal S^n \mid \mathcal X \succ 0\} S++n​={X∈Sn∣X≻0}
    同上:$\mathcal{X}\succ 0\iff {\mathcal{Z}}^T\mathcal{XZ}>0\forall \mathcal{Z}$

  对于集合${\mathcal{S}}_{+}^n$中的元素$\mathcal{X}$，它们必然是半正定矩阵。因而$\lambda \cdot \mathcal{X}(\forall \lambda \ge 0)$依然是半正定矩阵。因而满足锥集合的定义：
  $$\mathcal{X}\in {\mathcal{S}}_{+}^n\Rightarrow \lambda \cdot \mathcal{X}\in {\mathcal{S}}_{+}^n\lambda \ge 0$$
  因而集合${\mathcal{S}}_{+}^n$是锥集合。
  新的问题：锥集合${\mathcal{S}}_{+}^n$是不是凸集合$?$根据凸集合的定义，有：

  • 从集合${\mathcal{S}}_{+}^n$中任意选择一系列半正定矩阵：
    $$\forall x_1,x_2,\cdots ,x_k\in {\mathcal{S}}_{+}^n$$
  • 选择${\lambda }_i(i=1,2,\cdots ,k)$满足：
    $$\{\begin{array}{l}{\lambda }_i\ge 0i=1,2,\cdots ,k\\ {\sum }_{i=1}^k{\lambda }_i=1\end{array}$$
  • 观察：${\sum }_{i=1}^k{\lambda }_i\cdot x_i$中每一项${\lambda }_i\cdot x_i(i=1,2,\cdots ,k)$均是半正定矩阵，因而${\sum }_{i=1}^k{\lambda }_i\cdot x_i$必然也是半正定矩阵。即：
    $$\sum _{i=1}^k{\lambda }_i\cdot x_i\in {\mathcal{S}}_{+}^n$$
    因此锥集合${\mathcal{S}}_{+}^n$必然是凸集合。

  关于半定矩阵锥的图像，以二阶矩阵为例。如果二阶矩阵$\left(\begin{array}{c}xy\\ yz\end{array}\right)\in {\mathcal{S}}_{+}^2$，也就是说：该二阶矩阵是一个半正定矩阵。如何判定一个矩阵是半正定的$?$

  • 主对角线元素$x,z\ge 0$；
  • 该矩阵的顺序主子式：$x\cdot z-y^2\ge 0$；
  • 同样绘制它的图像：
    这里的图像不容易看，像个船头~大家自己多试试角度~

import numpy as np
import matplotlib.pyplot as plt
import tqdm

x = np.linspace(-5,5,20)
y = np.linspace(-5,5,20)
z = np.linspace(-5,5,20)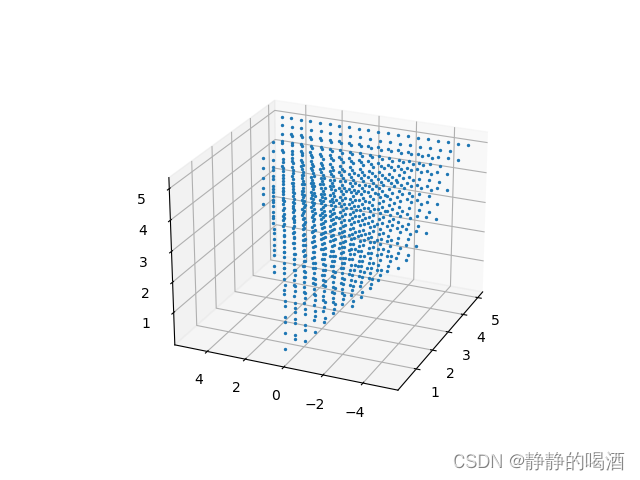![请添加图片描述](https://img-blog.csdnimg.cn/2fecd39719bc4af392e4cb9316296f6b.png)


def SequentialPrincipalMinor(x,y,z):
    return x * z - (y ** 2)

ax = plt.axes(projection='3d')
for i in tqdm(list(x)):
    for j in list(y):
        for k in list(z):
            if i >= 0 and k >= 0 and SequentialPrincipalMinor(i,j,k) >= 0:
                ax.scatter(i,j,k,c="tab:blue",s=2)
            else:
                continue
plt.show()

最终结果表示如下：

个人理解：集合${\mathcal{S}}_{++}^n$不仅是锥集合，并且也是凸集合。
这个图就不贴了，和上面的结果很像~

• 关于$\begin{array}{r}\sum _{i=1}^k{\lambda }_i\cdot x_i{x}_i\in {\mathcal{S}}_{++}^n\end{array}$，只要${\lambda }_i\cdot x_i(i=1,2,\cdots ,k)$中至少有一项是正定矩阵，那么$\begin{array}{r}\sum _{i=1}^k{\lambda }_i\cdot x_i\end{array}$必然是正定矩阵。
• 由于$\begin{array}{r}\sum _{i=1}^k{\lambda }_i=1\end{array}$，因而不可能出现${\lambda }_1={\lambda }_2=\cdots ={\lambda }_k=0$。也就是说：必然存在项${\lambda }_i>0$，从而使${\lambda }_i\cdot x_i$是正定矩阵。

$\text{Process}:43:34/1:21:31$
相关参考：
最优化理论与方法-第二讲-凸集
凸优化笔记1：凸集Convex Sets