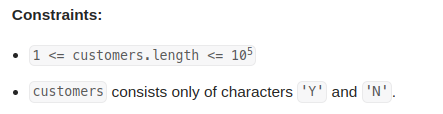Problem - H - Codeforces
题意:
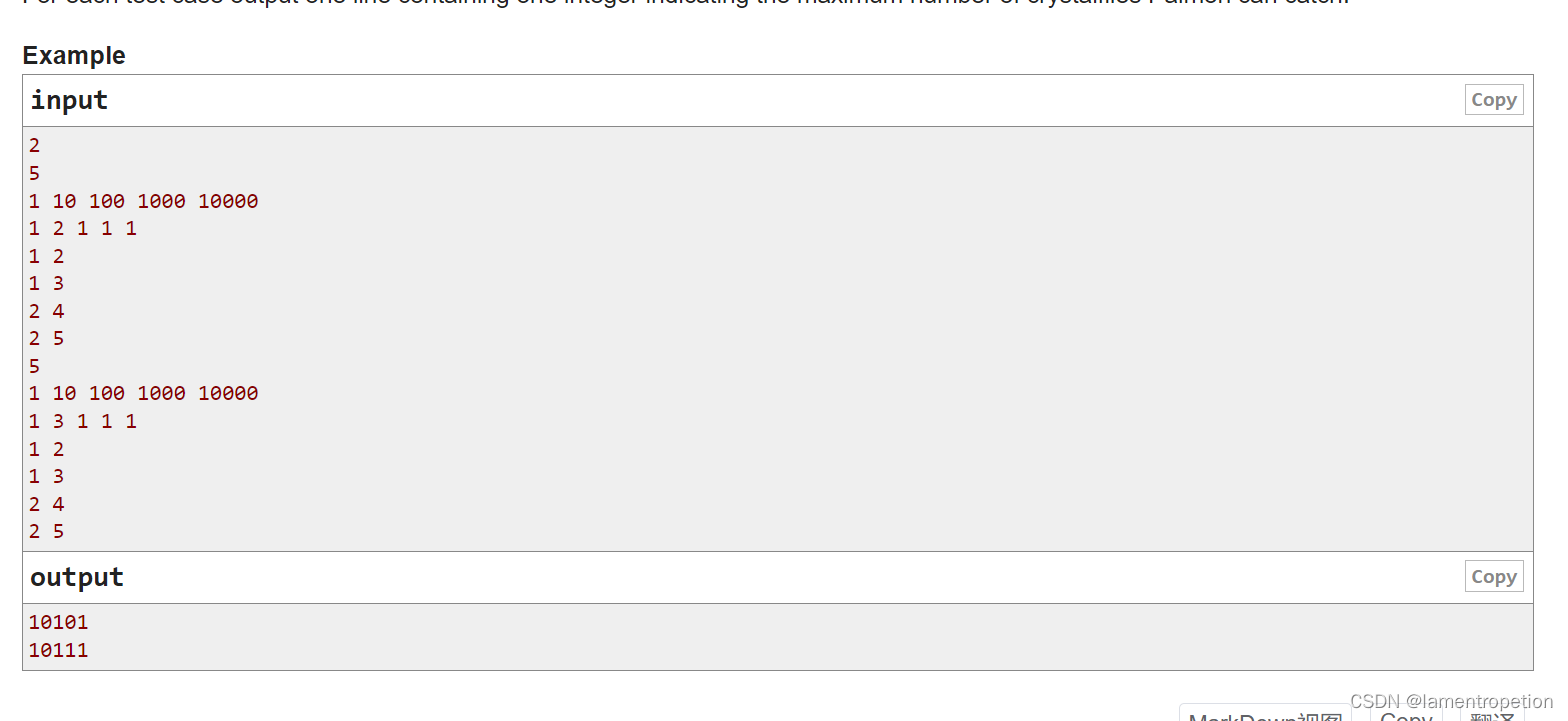
思路:
这题应该算是铜牌题
铜牌题 = 简单算法 + 基础思维
简单复盘一下思路
首先,我们发现有个很特殊的条件: ti <= 3
然后看一下样例:
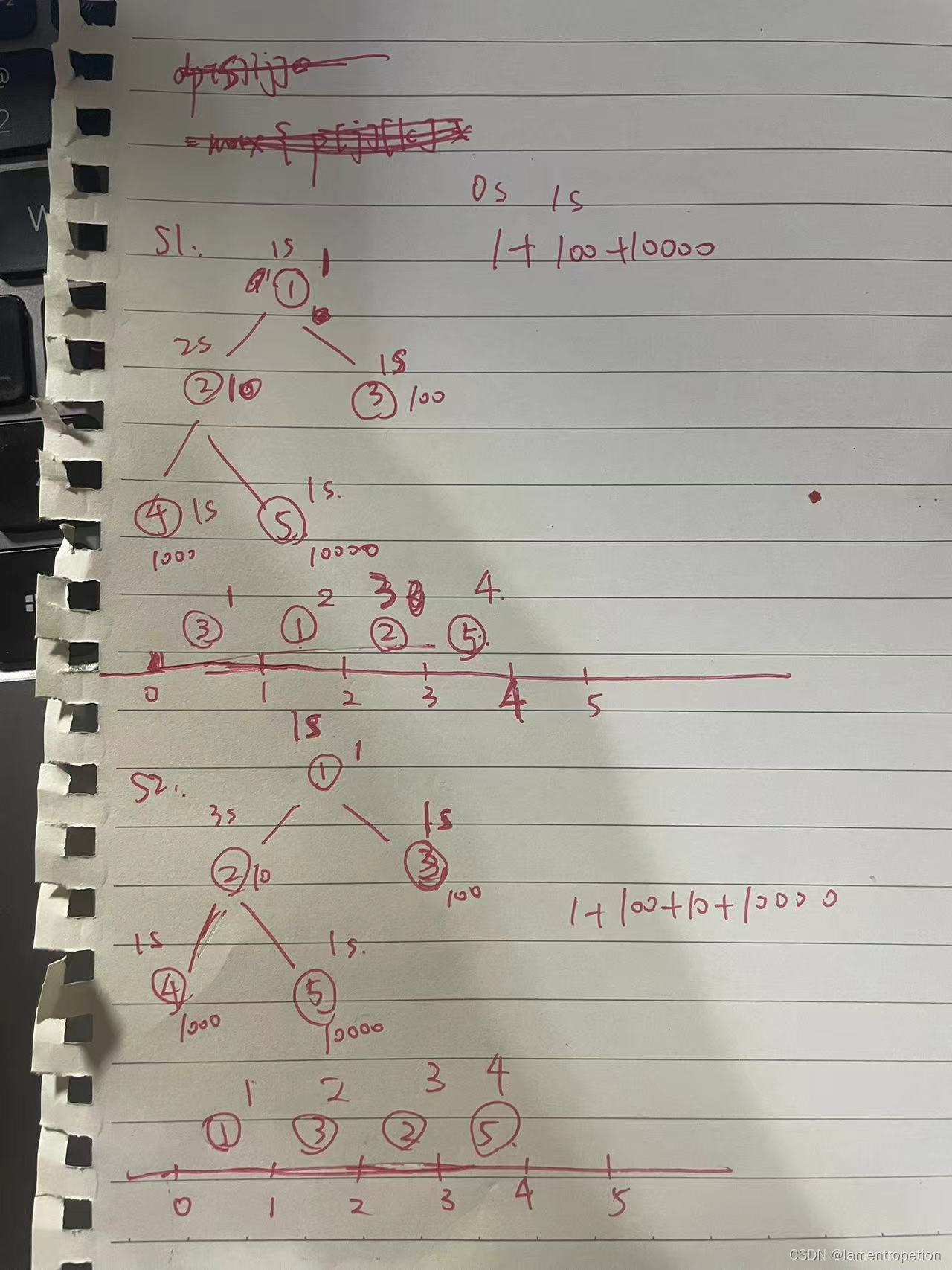
注意到,对于一个结点 u ,如果它的所有子节点中没有 tv = 3的,那么就肯定是沿着一棵子树走到底,然后去走剩下的子树
如果所有子节点中有 tv = 3的,那么可以先走到某个子节点,然后再走到这个 tv = 3的结点
注意到了子问题,那么很自然地去考虑树DP
注意到子问题可以分类成不算结点u 和 算结点u, 因此可以这样设计状态
设 dp[u] 为没有走过结点 u的这棵子树的贡献
然后考虑转移
因为 ti <= 3, 考虑在转移的时候暴力分讨
因为怎么转移和这些子节点中是否存在 tv = 3的结点有关,那么考虑先去把这些结点遍历一遍,看看是否存在,然后去转移
如果存在,那么就是先走到某个结点,再走到这个tv = 3的结点
考虑枚举这个“某个结点”,注意到tv = 3的结点可能会有多个,我们贪心地保留av最大的那个,这个可以考虑用multiset维护
为了计算贡献,我们设sum[u]表示所有子节点的 dp[v] 之和
此时的贡献为:
dp[u] = max{sum[u] - dp[v] + sum[v] + a[v] + *rbegin()}
然后考虑不存在tv = 3的结点,那么就是一次性走到底,再去遍历其他结点,此时贡献为 sum[u] + mx,其中 mx 为所有子节点中最大的 a[v]
为了防止出问题,我们在原来的multiset中先插入 -Inf
Code:
#include <bits/stdc++.h>
#define int long long
using i64 = long long;
constexpr int N = 1e5 + 10;
constexpr int M = 1e5 + 10;
constexpr int P = 2e2 + 10;
constexpr i64 Inf = 1e18;
constexpr int mod = 1e9 + 7;
constexpr double eps = 1e-6;
std::vector<int> adj[N];
int n;
int a[N], t[N];
int dp[N], sum[N];
void dfs(int u, int fa) {
std::multiset<int> S;
int mx = 0;
for (auto v : adj[u]) {
if (v == fa) continue;
dfs(v, u);
sum[u] += dp[v];
mx = std::max(mx, a[v]);
if (t[v] == 3) S.insert(a[v]);
}
dp[u] = sum[u] + mx;
S.insert(-0x3f3f3f3f);
for (auto v : adj[u]) {
if (v == fa) continue;
if (t[v] == 3) S.erase(S.find(a[v]));
dp[u] = std::max(dp[u], sum[u] - dp[v] + sum[v] + a[v] + (*S.rbegin()));
if (t[v] == 3) S.insert(a[v]);
}
}
void solve() {
std::cin >> n;
for (int i = 1; i <= n; i ++) {
sum[i] = dp[i] = 0;
adj[i].clear();
}
for (int i = 1; i <= n; i ++) {
std::cin >> a[i];
}
for (int i = 1; i <= n; i ++) {
std::cin >> t[i];
}
for (int i = 1; i <= n - 1; i ++) {
int u, v;
std::cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
dfs(1, -1);
std::cout << dp[1] + a[1] << "\n";
}
signed main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int t = 1;
std::cin >> t;
while (t--) {
solve();
}
return 0;
}