From Computational Problem to zk-SNARK
本部分就是将计算难题转换为多项式,然后使用zk-SNARK。
(注:以下用 P,V 替代 Prover,Verifier)
计算难题->R1CS
R1CS(Rank-1 Constraint System)是一种能够将算数电路统一成约束向量的方式,一组向量构成一组满足特定形式的式子。
计算式拆解
我们知道一般的计算可以拆解为 左操作数 操作符 右操作数 = 输出(如
a
×
b
=
c
a\times b = c
a×b=c)这样的格式,更复杂的计算则是由一系列简单的计算组合而成的。
那么多个操作符应该如何如何表示呢?
多个操作符就需要将其拆分成单个操作符组成式子组,以乘法为界限,例如假设某个计算难题的计算正确计算过程是
a
b
(
a
+
c
)
=
d
ab(a+c)=d
ab(a+c)=d这个计算式子,有两个乘法,那么就需要拆分成两个式子,如下
{
a
×
b
=
e
(
a
+
c
)
×
e
=
d
\begin{cases} {\color{green}a} \times {\color{blue}b} = {\color{red}e}\\ {\color{green}(a+c)} \times {\color{blue}e} = {\color{red}d} \end{cases}
{a×b=e(a+c)×e=d
单看单个操作符的话,绿色就代表
l
l
l,蓝色就是
r
r
r,红色则是
o
o
o。
事实上,这就是一个将计算过程化为算数电路的过程,三个颜色分别代表左,右输入和输出。电路中仅有乘法门和加法门,需要注意的是,加法不作为输出,而是直接作为乘法门的输入,这也符合前面提到的操作符以乘法为界限。
强调一下:这里的式子是代表的是某个计算难题的正确计算过程,也可以看作是 P 给 V 的proof 中应该要展示的,证明自己确实用的正确的计算过程。
转化为约束向量
接着把算数电路变换成满足特定形式的式子,如前面的例子
- 首先对上述式子组中的每一个式子(即,每一个电路门)都生成三个向量(分别称作左向量,右向量和出向量),其维度为不同变量的数目 (例子中为 5 个,每一维分别对应 a , b , c , d , e a,b,c,d,e a,b,c,d,e ), 记式子组式子的数目为 n n n, 记 l i , r i , o i , i ∈ [ n ] l_i,r_i,o_i,i\in [n] li,ri,oi,i∈[n]分别为第 i i i 个式子对应的左向量,右向量和出向量。用向量 v = ( v 1 , … , v m ) v=(v_1,\dots,v_m) v=(v1,…,vm) 表示 m m m个变量组成的向量,(如这里的 v = ( a , b , c , d , e ) v = (a,b,c,d,e) v=(a,b,c,d,e))
这里就是两个式子,两组共6个向量(每一组都分为左,右,输出三个向量)
- 向量构造方法是,如果该变量在式子里被使用,就设置为1,否则就设置为0,也就是变量有值即为1,否则为0。
以上面例子为例,可以构造出如下两组向量,每一行对应一个式子
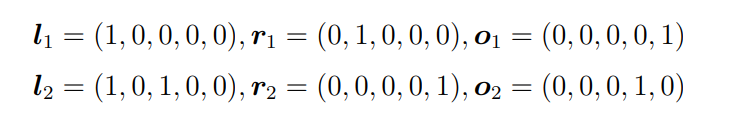
- 这时候把向量和 v v v作内积,那么左向量将得到式子的左操作数,右向量和输出向量同理,最终两组向量加上对应操作符将能还原出原式子组。
所以整个式子组便可以表示为
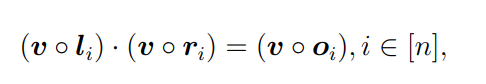
以上说明了也就是 P 知道原式子的解等价于他知道一组
v
v
v使得式子组成立。
从计算难题或者说复杂方程转换为特定形式的约束向量就叫做R1CS。
R1CS->QAP
QAP(Quadratic Arithmetic Program):二次算数程序,通俗的说就是给定一系列的多项式以及一个目标多项式,这个集合就是QAP。要达到的目的就是,是否能根据这一系列的多项式,求得它们的一个线性组合,刚好可以整除目标多项式。
转化多项式的思路hint
先从单个操作符的计算式子说起,左操作数 操作符 右操作数 = 输出(如
a
×
b
=
c
a\times b = c
a×b=c)。操作数代表就是实际常量值。
我们知道多项式的计算有不错的算术特性,就是计算某点的值的时候,先带入值计算和先计算再带入值得到的结果是相同的。所以如果我们将操作数表示为多项式的话,同样可以得到经过操作符计算后的结果,那么我们就可以用多项式在某一点的取值去替代掉原来的操作数值。
也就是找到一个多项式
l
(
x
)
o
p
e
r
a
t
o
r
r
(
x
)
=
o
(
x
)
l(x) \ \mathrm{operator} \ r(x) = \ o(x)
l(x) operator r(x)= o(x),它满足
l
(
a
)
o
p
e
r
a
t
o
r
r
(
a
)
=
o
(
a
)
l(a) \ \mathrm{operator} \ r(a) = \ o(a)
l(a) operator r(a)= o(a)即,
l
(
x
)
l(x)
l(x)可以代表在
x
=
a
x=a
x=a的时候的左操作数,剩下
r
(
x
)
,
o
(
x
)
r(x),o(x)
r(x),o(x)同理,如果将
a
a
a代入,就可以得到一般的计算常量式子。一组多项式就会对应这样一个特殊点。
怎么把这里的这种多项式和前面的多项式证明联系起来呢?这里先给一个小小的问题转化思路提示😇,很简单,以只有一个操作符的式子为例,做一个移项,就可以得到
l
(
x
)
o
p
e
r
a
t
o
r
r
(
x
)
−
o
(
x
)
=
0
l(x) \ \mathrm{operator} \ r(x) - \ o(x) = 0
l(x) operator r(x)− o(x)=0
这个式子在
x
=
a
x = a
x=a为解的情况下该式子就等于 0。也就是计算式计算正确等价于改变后的多项式有特殊解,即必须具有根
x
=
a
x = a
x=a,等价于因式分解后必须含有
(
x
−
a
)
(x-a)
(x−a)这一项。
这样就将一般计算式计算结果的正确性转变为了多项式的结果,某个多项式包含因式,这个因式不就是前面多项式证明里提到的目标多项式
t
(
x
)
=
(
x
−
a
)
t(x) = (x-a)
t(x)=(x−a)吗?
单个多项式的验证
我们可以定义
p
(
x
)
=
t
(
x
)
h
(
x
)
=
l
(
x
)
×
r
(
x
)
−
o
(
x
)
p(x)=t(x)h(x)=l(x) \times r(x)-o(x)
p(x)=t(x)h(x)=l(x)×r(x)−o(x),移项后即
l
(
x
)
×
r
(
x
)
=
t
(
x
)
h
(
x
)
+
o
(
x
)
l(x) \times r(x) = t(x)h(x)+o(x)
l(x)×r(x)=t(x)h(x)+o(x)
那么结合前面多项式的证明,证明多项式成立,仅需要证明多项式在某点
s
s
s的取值成立即可,使用paring 方法, V 的验证变为
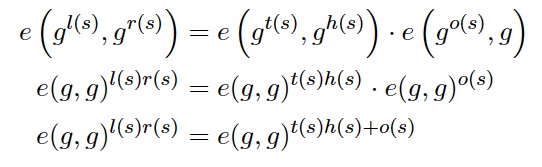
整体的方案变为

这就是单个操作符乘号的证明思路。
不完整的多个多项式的验证
前面说到多个操作符需要拆分为多个单操作符式子,那么一个式子就可以对应转化为一组
l
i
(
x
)
o
p
e
r
a
t
o
r
r
i
(
x
)
=
o
i
(
x
)
l_i(x) \ \mathrm{operator} \ r_i(x) = \ o_i(x)
li(x) operator ri(x)= oi(x),这样就有多组多项式了,那就会对应多个特殊点。
那么如何验证多组多项式呢?
一个最简单的方法就是对单个式子挨个儿进行验证,这显然会使得验证复杂度变得很高,如果能够统一到一个多项式里,那么效率会大大提高。(实际上就是需要统一到一个多项式 )
那么先假设我们已经构造出了这样的多项式(怎么构造下节再说)
像前面一样,前面提到,可以将操作式变为
p
(
x
)
=
l
(
x
)
×
r
(
x
)
=
t
(
x
)
h
(
x
)
+
o
(
x
)
p(x)=l(x) \times r(x)=t(x)h(x)+o(x)
p(x)=l(x)×r(x)=t(x)h(x)+o(x)来将操作数式子的正确性转变为多项式在某点的结果为0。
以前面的有三个操作符的例子为例,如假设特殊点
x
=
z
i
,
i
∈
{
1
,
2
,
3
}
x = z_i,i\in \{1,2,3\}
x=zi,i∈{1,2,3}时(事实上是可以任意值,这里假设就是1,2,3),整体的多项式结果会是0,也就是说多项式有
x
=
1
,
2
,
3
x=1,2,3
x=1,2,3这样三个解,即可以得到
t
(
x
)
=
(
x
−
1
)
(
x
−
2
)
(
x
−
3
)
t(x)=(x-1)(x-2)(x-3)
t(x)=(x−1)(x−2)(x−3)。。
那么得到
t
(
x
)
t(x)
t(x)后,证明者 P 就可以计算出
h
(
x
)
h(x)
h(x),从而仿造前面单个式子的协议就可以给出证明。
So,接下来的目标很明确,那就是结合前面的 R1CS 向量表达构造出这样的多项式。
多项式构造
我们知道的是每组
l
i
(
x
)
o
p
e
r
a
t
o
r
r
i
(
x
)
=
o
i
(
x
)
l_i(x) \ \mathrm{operator} \ r_i(x) = \ o_i(x)
li(x) operator ri(x)= oi(x)中,一组多项式就对应了一个特殊点,那么多组多项式就会对应多个特殊点,一组多项式满足一个计算式,多组多项式就满足多个计算式,所以一个拥有多个特殊点的多项式,就可以满足多个计算式,也就可以代表整个计算过程。构造多项式就是找到一个多项式(一根曲线)通过了那些特殊点。
以
l
(
x
)
l(x)
l(x)为例,如将特殊值
x
=
z
i
,
i
∈
{
1
,
2
,
3
}
x = z_i,i\in \{1,2,3\}
x=zi,i∈{1,2,3}作为横坐标(假设就是1,2,3),将
l
i
(
1
)
,
l
i
(
2
)
,
l
i
(
3
)
l_i(1),l_i(2),l_i(3)
li(1),li(2),li(3)的值作为纵坐标,即点
(
1
,
l
i
(
1
)
)
,
(
2
,
l
i
(
2
)
)
,
(
2
,
l
i
(
2
)
)
(1,l_i(1)),(2,l_i(2)),(2,l_i(2))
(1,li(1)),(2,li(2)),(2,li(2))。(
r
i
(
x
)
,
o
i
(
x
)
r_i(x),o_i(x)
ri(x),oi(x)同理),这就构成了点,由基本的数学定理可以知道,
n
n
n个点可以构成一个唯一的
n
−
1
n-1
n−1阶的多项式。联立所有的点就可以通过类似拉格朗日插值法合并出一个总的多项式。
举个例子
以
2
×
1
×
3
×
2
=
12
2 \times 1 \times 3 \times 2 =12
2×1×3×2=12这个计算为例,三个操作符,将其拆分为三个
l
e
f
t
×
r
i
g
h
t
=
o
u
t
p
u
t
left \ \times \ right = \ output
left × right= output的形式
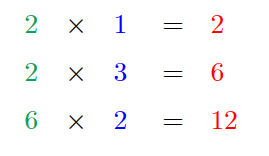
这里有三个式子,也就是
x
=
z
i
,
i
∈
{
1
,
2
,
3
}
x = z_i,i\in \{1,2,3\}
x=zi,i∈{1,2,3}(假设就是1,2,3),意味着有三组操作数
(
l
(
i
)
,
r
(
i
)
,
o
(
i
)
)
(l(i),r(i),o(i))
(l(i),r(i),o(i)),进而可以形成三组点
{
l
(
x
)
:
(
1
,
2
)
,
(
2
,
2
)
,
(
3
,
6
)
r
(
x
)
:
(
1
,
1
)
,
(
2
,
3
)
,
(
3
,
2
)
o
(
x
)
:
(
1
,
2
)
,
(
2
,
6
)
,
(
3
,
12
)
\begin{cases} l(x):(1,2),(2,2),(3,6)\\ r(x):(1,1),(2,3),(3,2)\\ o(x):(1,2),(2,6),(3,12) \end{cases}
⎩
⎨
⎧l(x):(1,2),(2,2),(3,6)r(x):(1,1),(2,3),(3,2)o(x):(1,2),(2,6),(3,12)
现在想一想我们要做什么?那就是如何找出能够通过这些点的三个多项式。以
l
(
x
)
l(x)
l(x)为例,我们知道两个点可以解出一个唯一的一次式子,那么
n
n
n个点,就可以唯一的确定一个
n
−
1
n-1
n−1阶多项式,所以最后的
l
(
x
)
l(x)
l(x)会是一个
n
−
1
n-1
n−1阶多项式。
可以计算出
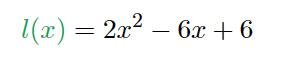
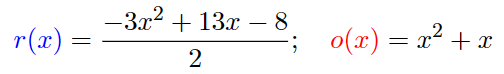
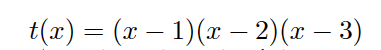
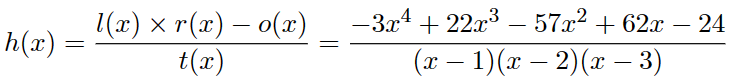
BUT!注意到在之前的协议中,Setup 阶段限制好了多项式的阶数,Proving 阶段会生成多项式的系数 ,P 能拿到
(
g
s
i
,
g
α
s
i
)
(g^{s_i},g^{\alpha s_i})
(gsi,gαsi),这就意味着 P 对多项式是有绝对控制权的,也就他可以随意生成多项式,那么他完全有可能生成奇奇怪怪的多项式从而计算毫不相干的东西,同样能够满足 V 的 paring 验证,从而破坏掉协议的一致性。
这就像P 向 V 证明,他知道某个难题的解,但是 P 到底没有使用正确的计算方法去计算,V 是无从得知无法验证到的,万一他计算的其他毫不相关的东西呢?
前面的协议中 Verification 阶段只能验证到 P 确实是按照某个多项式进行计算的,但不知道是不是想要的那个,毕竟验证过程里只涉及到了
α
−
s
h
i
f
t
\alpha -shift
α−shift这个用来限制多项式格式的,仅能验证到确实是用了某个多项式,做了相似但不相关的计算。
所以,得保证 P 用的确实是正确的计算方法,也就是需要每个计算式都要满足,顺序不重要,最后结果对就行。
一个解决方案是,把每个生成的多项式加密放到 Setup 阶段去公开,大家都能看到。
然后在 Proving 阶段,让 P 只能用自己知道的解去组合调用这些多项式,生成 proof,这样就可以确保 P 确实是用正确的多项式,达到一致性。(验证方法在后面)
(Wait,不会有人认为,为什么不直接把最终的多项式放到 Setup 阶段吧?那不是谁都可
以证明了吗?那协议还有啥意义呢?)
基础多项式的构造
我们要构造的是满足在特殊点能得到对应结果值(也就是 P 持有的解)的多项式,构造多项式的时候需要用到特殊值以及对应多项式结果组成的点,而解又不能够直接呈现在 Setup 阶段的,而是让 P 在 Proving 阶段再用。所以不能直接生成目标多项式,需要拆开。
于是可以利用多项式的性质,比如我们想得到一个结果为
a
a
a的式子,就可以先构造一个结果为 1 的多项式,然后再乘以
a
a
a,这样就能达到目的了。
假设目标结果为
a
a
a的多项式如下图,
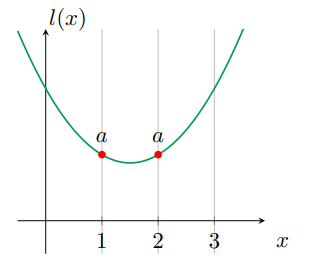
我们设定的结果为1的基准多项式为,
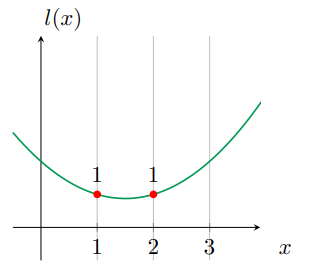
把生成的基准多项式放到 Setup 阶段,那么Proving 阶段就仅需带入自己知道的解,就可以完成目标结果的计算了。
(Wait again,为什么不把完整的基准多项式放到 Setup 里呢?因为组合成完整的多项式需要对每个基准多项式乘以对应的系数,介个只有 P 有)
注意到,计算过程的每一步,每个式子都会转换为一组多项式
l
i
(
x
)
o
p
e
r
a
t
o
r
r
i
(
x
)
=
o
i
(
x
)
l_i(x) \ \mathrm{operator} \ r_i(x) = \ o_i(x)
li(x) operator ri(x)= oi(x),前面也提到了,如果式子一个一个的验证的话会导致效率很低,所以为了一步到位,我们需要将它们组合成一组整体的多项式,像
L
(
x
)
o
p
e
r
a
t
o
r
R
(
x
)
=
O
(
x
)
L(x) \ \mathrm{operator} \ R(x) = \ O(x)
L(x) operator R(x)= O(x)这样,一次就能达成目的。
那么接下来就是构造出结果为1的多项式了。
注意到多项式的算术性质决定了我们可以使用多个同阶的多项式叠加出需要的多项式。
以下面计算式的左操作数为例,左边有两种,三个变量。
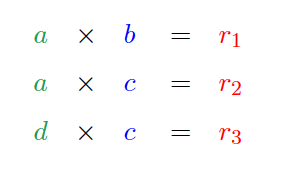
想转化出来的
l
(
x
)
l(x)
l(x)是一个在
x
=
1
,
x
=
2
,
x
=
3
x=1,x=2,x=3
x=1,x=2,x=3,分别取值
l
(
1
)
=
a
,
l
(
2
)
=
a
,
l
(
3
)
=
b
l(1)=a,l(2)=a,l(3)=b
l(1)=a,l(2)=a,l(3)=b的二阶多项式。如图
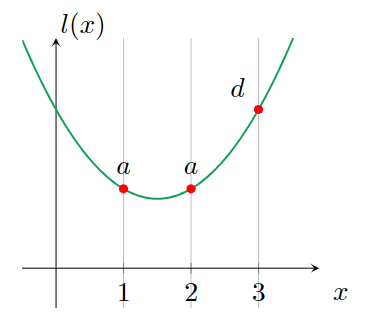
三个式子会得到三个
l
i
(
x
)
l_i(x)
li(x),比如第一个多项式
l
1
(
x
)
l_1(x)
l1(x),它是个二阶多项式,让它在
x
=
1
x=1
x=1取值为1,在其它
x
=
2
,
3
x=2,3
x=2,3时取值为0; 第二个多项式
l
2
(
x
)
l_2(x)
l2(x),让它在
x
=
2
x=2
x=2取值为1,在其它
x
=
1
,
3
x=1,3
x=1,3时取值为0;第三个多项式
l
3
(
x
)
l_3(x)
l3(x),让它在
x
=
3
x=3
x=3取值为1,在其它
x
=
1
,
2
x=1,2
x=1,2时取值为0。
即三个多项式通过如下点
{
l
1
(
x
)
:
(
1
,
1
)
,
(
2
,
0
)
,
(
3
,
0
)
l
2
(
x
)
:
(
1
,
0
)
,
(
2
,
1
)
,
(
3
,
0
)
l
3
(
x
)
:
(
1
,
0
)
,
(
2
,
0
)
,
(
3
,
1
)
\begin{cases} l_1(x):(1,1),(2,0),(3,0)\\ l_2(x):(1,0),(2,1),(3,0)\\ l_3(x):(1,0),(2,0),(3,1) \end{cases}
⎩
⎨
⎧l1(x):(1,1),(2,0),(3,0)l2(x):(1,0),(2,1),(3,0)l3(x):(1,0),(2,0),(3,1)
这样三个多项式就可以通过类似拉格朗日插值法求出来,每个多项式仅在对应点有意义,在其它点无意义,然后直接加法叠加即可得到结果为1的多项式。还记得R1CS吧?得到
l
1
,
l
2
l_1,l_2
l1,l2的向量就是为了辅助完成得到这个多项式。
注意到第一个和第二个都是需要得到结果为
a
a
a的多项式,所以可以合并起来同时乘以
a
a
a。于是都乘以解后,可以得到最终的多项式
L
(
s
)
=
a
l
a
(
s
)
+
b
l
b
(
s
)
L(s)=al_a(s)+bl_b(s)
L(s)=ala(s)+blb(s)。
R1CS中,P 知道原式子的解转换为等价于他知道一组解
v
v
v,(这是解哦),把原式子转化为多项式后,带入这组解就变成能计算出正确结果的多项式,这就和上面对应了。可以以同样的方式构造出
R
(
x
)
,
O
(
x
)
R(x),O(x)
R(x),O(x)
R1CS就可以转换为类似下面这种形式
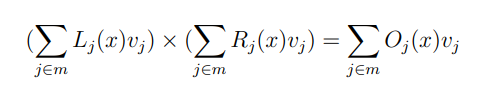
更加复杂的多项式构造
目前为止,我们的操作符都是以单个乘法
×
\times
×为例的,没有涉及到更加复杂的计算组合,那么下面介绍一下复杂的计算如何转换为多项式。
- 最简单的加法,比如 ( a + c ) × b = r {\color{green}(a+c)} \times {\color{blue}b} = {\color{red}r} (a+c)×b=r这样的,显然,我们前面构造多项式的方法,是可以允许加法的,只要确保构造单个多项式的时候,满足仅有单个使用的变量具有非零值,而其他变量的都为 0 就可以了。
- 变量含有常数系数,如 3 a × 2 b = 6 r {\color{green}3a} \times {\color{blue}2b} = {\color{red}6r} 3a×2b=6r,以前构造基准多项式的时候,选择的是取值是 1,这里选择成对应的常数即可,如, l a ( x ) = 3 l_a(x) = 3 la(x)=3,这样再乘以变量就可以还原。
- 变量加法,比如 a + c = r {\color{green}a+c} = {\color{red}r} a+c=r,我们可以转变为 ( a + c ) × 1 = r {\color{green}(a+c)} \times {\color{blue}1} = {\color{red}r} (a+c)×1=r,后续和前面一样。
- 变量减法,如 ( a − b ) × 1 = r {\color{green}(a-b)} \times {\color{blue}1} = {\color{red}r} (a−b)×1=r,可以向常数系数那样,把取值1,设置为 -1,然后变成一般加法,就像这样 ( a + ( − 1 × b ) ) × 1 = r {\color{green}(a+(-1 \times b))} \times {\color{blue}1} = {\color{red}r} (a+(−1×b))×1=r。
- 变量除法,如 a ÷ b = r {\color{green}a} \div {\color{blue}b} = {\color{red}r} a÷b=r,可以调换一下顺序,变成乘法如, b × r = a {\color{green}b} \times {\color{blue}r} = {\color{red}a} b×r=a。
将更加复杂的问题转换为多项式
- 范围证明,如证明 0 ≤ a ≤ 15 0 \le a \le 15 0≤a≤15,那么可以引入限制式 a = 8 a 3 + 4 a 2 + 2 a 1 + a 0 a = 8a_3+4a_2+2a_1+a_0 a=8a3+4a2+2a1+a0,然后再引入限制式 a i a_i ai等于0或者1即可。
- 证明一个数 a a a是1还是0,可以引入限制式 a ( a − 1 ) = 0 a(a-1)=0 a(a−1)=0。
- 取模函数,可引入 a = k b + r a=kb+r a=kb+r。
等等。。
结合多项式验证和多项式构造步骤,找到所有的
{
l
i
(
x
)
,
r
i
(
x
)
,
o
i
(
x
)
}
i
∈
{
1
,
…
,
n
}
\{l_i(x),r_i(x),o_i(x)\}_{i\in\{1,\dots,n\}}
{li(x),ri(x),oi(x)}i∈{1,…,n}和目标多项式
t
(
x
)
t(x)
t(x)的步骤就称为 QAP。
多项式验证
至此,我们已经构造出了多项式,现在继续多项式验证。前面提到过不完整的验证思路,为什么不完整呢?仅对最后的合并多项式进行检验并不能保证检验的多项式就是目标那个。
因为没有对多项式进行限制的话,那即便是把多项式生成交到 Setup 阶段完成,P 在 Proving 阶段还是可以对 Setup 阶段预定的多项式进行更改的。
所以还需要对此进行限制,强制让 P 使用预定好的多项式。
那么会分有以下情况,
修改多项式
以
L
(
x
)
L(x)
L(x)为例,理想情况下,我们希望它是由 P 通过 Setup 阶段预先设定好的
l
i
(
x
)
l_i(x)
li(x)线性组合出来的。
还记得前面的多项式证明里提到的
α
−
s
h
i
f
t
\alpha - shift
α−shift,这个用来限定多项式的方法,它可以限定多项式的指数,这里同样适用。
回顾一下多项式证明协议的 proving key 和 verification key
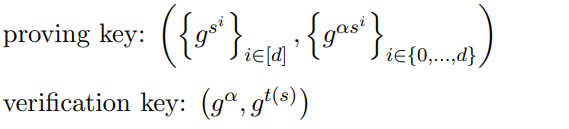
那么 Setup 阶段的Proving key 变成
g
l
a
(
s
)
,
g
α
l
a
(
s
)
g^{l_a(s)},g^{\alpha l_a(s)}
gla(s),gαla(s),P 能够获取到的就是 proving 和 verification key,即
g
l
a
(
s
)
,
g
α
l
a
(
s
)
,
g
α
,
g
s
k
g^{l_a(s)},g^{\alpha l_a(s)},g^\alpha,g^{s^k}
gla(s),gαla(s),gα,gsk。
对一个单一的基准多项式来说,
- 由于多项式有了加密且不知道 s s s,那么简单修改多项式系数是不可能的;
- 也不能在里面新增一个预定的多项式,因为 s s s不能直接使用,能用的是 g s k g^{s^k} gsk,如果新增的多项式为 r ( x ) r(x) r(x)的话,意味着只能计算得到 g r ( s ) g^{r(s)} gr(s)而得不到 r ( s ) r(s) r(s)。注意,P 也是不知道 α \alpha α的, g α l a ( x ) , g r ( s ) , g α g^{\alpha l_a(x)},g^{r(s)},g^\alpha gαla(x),gr(s),gα是无法产生 g α r ( s ) g^{\alpha r(s)} gαr(s)的,那么势必会破坏掉 α − s h i f t \alpha - shift α−shift。
所以只能修改整体的多项式的比例,也就是乘以一个常数系数。
对一个组合后的多项式来说,同样可以达到效果,假设 Setup 阶段提供的Proving key 为
(
g
l
a
(
s
)
,
g
α
l
a
(
s
)
,
g
l
d
(
s
)
,
g
α
l
d
(
s
)
)
(g^{l_a(s)},g^{\alpha l_a(s)},g^{l_d(s)},g^{\alpha l_d(s)})
(gla(s),gαla(s),gld(s),gαld(s))两组,那么就可以得到
g
α
L
(
x
)
=
g
α
l
a
(
s
)
×
g
α
l
d
(
s
)
=
g
α
(
l
a
(
s
)
+
l
d
(
s
)
)
g^{\alpha {L(x)}} = g^{\alpha l_a{(s)}} \times g^{\alpha l_d(s)} = g^{\alpha (l_a(s)+l_d(s))}
gαL(x)=gαla(s)×gαld(s)=gα(la(s)+ld(s))。
但是可能会存在这样一种情况,也就是产生任意的式子,绕过验证,如
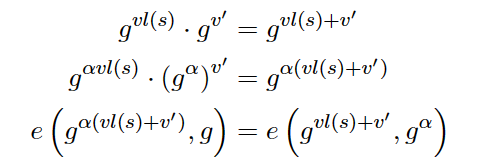
这个后面会提如何解决。
漏或者新增预定的多项式
有两种可能的情况就是,P 可以选择漏掉一个
g
l
a
(
s
)
g^{l_a(s)}
gla(s),或者重复多次用
g
l
a
(
s
)
g^{l_a(s)}
gla(s),得到
g
α
L
(
x
)
=
g
α
l
a
(
s
)
×
g
α
l
a
(
s
)
×
g
α
l
d
(
s
)
=
g
α
(
2
l
a
(
s
)
+
l
d
(
s
)
)
g^{\alpha {L(x)}} =g^{\alpha l_a{(s)}} \times g^{\alpha l_a{(s)}} \times g^{\alpha l_d(s)} = g^{\alpha (2l_a(s)+l_d(s))}
gαL(x)=gαla(s)×gαla(s)×gαld(s)=gα(2la(s)+ld(s))。这会有什么影响呢?事实上,这是无关紧要的。
先看看漏掉一个的情况,假设漏掉一个
g
l
a
(
s
)
g^{l_a(s)}
gla(s),那么我们知道一个
l
i
(
x
)
l_i(x)
li(x)对应的是一组
l
i
(
x
)
o
p
e
r
a
t
o
r
r
i
(
x
)
=
o
i
(
x
)
l_i(x) \ \mathrm{operator} \ r_i(x) = \ o_i(x)
li(x) operator ri(x)= oi(x),也就会对应一个计算式,同时也对应了一个解
t
i
(
x
)
=
(
x
−
i
)
t_i(x)=(x-i)
ti(x)=(x−i)。要知道 P 是不知道
t
(
x
)
t(x)
t(x)的,而 V 知道,那么漏掉一个
l
a
(
x
)
l_a(x)
la(x),就会导致
t
(
x
)
t(x)
t(x)漏掉一个解
t
a
(
x
)
=
(
x
−
a
)
t_a(x)=(x-a)
ta(x)=(x−a),那验证
p
(
x
)
=
h
(
x
)
t
(
x
)
p(x) = h(x)t(x)
p(x)=h(x)t(x)的时候,就肯定会失败。
同样如果多次重复使用,可以看到多项式会变成
g
α
(
2
l
a
(
s
)
+
l
d
(
s
)
)
g^{\alpha (2l_a(s)+l_d(s))}
gα(2la(s)+ld(s)),但得注意到
l
a
(
x
)
l_a(x)
la(x)和
2
l
a
(
x
)
2l_a(x)
2la(x)对应的解其实是一样的,所以无所谓啦。
多项式复用
比如
o
(
x
)
×
l
(
x
)
=
r
(
x
)
o(x) \times l(x) = r(x)
o(x)×l(x)=r(x) ,
L
(
x
)
=
l
a
(
x
)
+
r
b
(
x
)
+
o
c
(
x
)
L(x)=l_a(x)+r_b(x)+o_c(x)
L(x)=la(x)+rb(x)+oc(x),
l
(
x
)
×
l
(
x
)
=
o
(
x
)
l(x) \times l(x) = o(x)
l(x)×l(x)=o(x)d等等情况。
同样可以通过验证。原因就是使用了同一个
α
−
s
h
i
f
t
\alpha - shift
α−shift,所以需要对左右输入和输出使用不同的偏移量,即使用多个
α
−
s
h
i
f
t
\alpha - shift
α−shift,即
α
l
,
α
r
,
α
o
\alpha_l,\alpha_r,\alpha_o
αl,αr,αo。验证的时候分别验证即可。
那么此时的协议就会变成

变量不一致
注意到 V 在 verification phase 中,仅用 paring 去检验了多项式是否满足
α
−
s
h
i
f
t
\alpha - shift
α−shift。多项式的线性组合系数(变量)是否合适并不能检测到。
那么可能会存在变量不一致的情况,也就是
(
g
l
i
(
s
)
)
v
i
,
(
g
r
i
(
s
)
)
v
i
,
(
g
o
i
(
s
)
)
v
i
(g^{l_i(s)})^{v_i},(g^{r_i(s)})^{v_i},(g^{o_i(s)})^{v_i}
(gli(s))vi,(gri(s))vi,(goi(s))vi中的
v
i
v_i
vi,它有可能是不一致的,不一致就会导致某一步中计算的式子不是正确的,而这个按照前面的检验方式也是检测不出来的。
又是类似限制多项式问题,我们可以设立类似
α
−
s
h
i
f
t
\alpha - shift
α−shift的操作,强制让其使用相同的变量,也就是控制比例。如下,用
β
−
s
h
i
f
t
\beta - shift
β−shift来限制整体的系数必须是一样的。
(
g
l
i
(
s
)
)
v
L
,
i
,
(
g
r
i
(
s
)
)
v
R
,
i
,
(
g
o
i
(
s
)
)
v
O
,
i
,
(
g
β
(
l
i
(
s
)
+
r
i
(
s
)
+
o
i
(
s
)
)
)
v
B
,
i
\left(g^{l_i(s)}\right)^{v_{\mathrm{L},i}},\left(g^{r_i(s)}\right)^{v_{\mathrm{R},i}},\left(g^{o_i(s)}\right)^{v_{\mathrm{O},i}},\left(g^{\beta(l_i(s)+r_i(s)+o_i(s))}\right)^{v_{\mathcal{B},i}}
(gli(s))vL,i,(gri(s))vR,i,(goi(s))vO,i,(gβ(li(s)+ri(s)+oi(s)))vB,i
也就是
v
L
,
i
=
v
R
,
i
=
v
O
,
i
=
v
β
,
i
v_{L,i} = v_{R,i} = v_{O,i} = v_{\beta,i}
vL,i=vR,i=vO,i=vβ,i,验证方式如下
e
(
g
v
l
,
i
⋅
l
i
(
s
)
⋅
g
v
R
,
i
⋅
r
i
(
s
)
⋅
g
v
O
,
i
⋅
o
i
(
s
)
,
g
β
)
=
e
(
g
v
B
,
i
⋅
β
(
l
i
(
s
)
+
r
i
(
s
)
+
o
i
(
s
)
)
,
g
)
e\left(g^{v_{\mathrm{l},i}\cdot l_i(s)}\cdot g^{v_{\mathrm{R},i}\cdot r_i(s)}\cdot g^{v_{\mathrm{O},i}\cdot o_i(s)},g^\beta\right)=e\left(g^{v_{\mathrm{B},i}\cdot\beta(l_i(s)+r_i(s)+o_i(s))},g\right)
e(gvl,i⋅li(s)⋅gvR,i⋅ri(s)⋅gvO,i⋅oi(s),gβ)=e(gvB,i⋅β(li(s)+ri(s)+oi(s)),g)
BUT,也有特殊情况,如
l
i
(
s
)
,
r
i
(
s
)
,
o
i
(
s
)
l_i(s),r_i(s),o_i(s)
li(s),ri(s),oi(s)之间存在相等或者整除之类的关系的话,此时的变量就可以不用一定相等,如假设
l
i
(
s
)
=
r
i
(
s
)
=
w
,
y
=
o
(
s
)
l_i(s)=r_i(s)=w,y= o(s)
li(s)=ri(s)=w,y=o(s),对应的式子变为
β
(
v
L
w
+
v
R
w
+
v
O
y
)
=
v
β
⋅
β
(
w
+
w
+
y
)
\beta(v_\mathrm{L}w+v_\mathrm{R}w+v_\mathrm{O}y)=v_\mathrm{\beta}\cdot\beta(w+w+y)
β(vLw+vRw+vOy)=vβ⋅β(w+w+y),此时设
v
β
=
v
O
,
v
L
=
2
v
O
−
v
R
v_\beta = v_O,v_L = 2v_O-v_R
vβ=vO,vL=2vO−vR
显然变量是可以不等的,比如赋值
v
L
,
v
R
,
v
O
=
1
,
3
,
2
v_L,v_R,v_O = 1,3,2
vL,vR,vO=1,3,2。但是代入式子可以推出
β
(
2
v
O
w
−
v
R
w
+
v
R
w
+
v
O
y
)
=
v
O
⋅
β
(
2
w
+
y
)
=
v
β
⋅
β
(
2
w
+
y
)
\beta(2v_\mathrm{O}w-v_\mathrm{R}w+v_\mathrm{R}w+v_\mathrm{O}y)=v_\mathrm{O}\cdot\beta(2w+y)=v_\beta\cdot\beta(2w+y)
β(2vOw−vRw+vRw+vOy)=vO⋅β(2w+y)=vβ⋅β(2w+y)
则可以通过验证。
所以为了防止这种情况,需要将不同的式子用不同的
β
−
s
h
i
f
t
\beta - shift
β−shift,这样就可以保证即便有倍数或者相等关系,每一个分量也不会成比例。假设有三个,那么 V 需要三个
β
l
,
β
r
,
β
o
\beta_l,\beta_r,\beta_o
βl,βr,βo,用它们对值进行线性组合得到
β
l
l
i
(
s
)
+
β
r
l
r
(
s
)
+
β
o
l
o
(
s
)
\beta_l l_i(s)+\beta_r l_r(s)+\beta_o l_o(s)
βlli(s)+βrlr(s)+βolo(s),此时 P 需要向 V 提供一组同样符合
s
h
i
f
t
shift
shift的线性组合,由于不知道具体的
β
i
\beta_i
βi,故只能采用乘以相同的系数来完成要求。
P 可以计算
g
z
i
(
s
)
=
(
g
β
l
l
i
(
s
)
+
β
r
r
i
(
s
)
+
β
o
o
i
(
s
)
)
v
i
g^{z_i(s)}=\left(g^{\beta_ll_i(s)+\beta_rr_i(s)+\beta_oo_i(s)}\right)^{v_i}
gzi(s)=(gβlli(s)+βrri(s)+βooi(s))vi然后得到
g
Z
(
s
)
=
∏
i
=
1
n
g
z
i
(
s
)
=
g
β
l
L
(
s
)
+
β
r
R
(
s
)
+
β
o
O
(
s
)
g^{Z(s)}=\prod_{i=1}^ng^{z_i(s)}=g^{\beta_lL(s)+\beta_rR(s)+\beta_oO(s)}
gZ(s)=∏i=1ngzi(s)=gβlL(s)+βrR(s)+βoO(s)
验证
e
(
g
L
,
g
β
l
)
⋅
e
(
g
R
,
g
β
r
)
⋅
e
(
g
O
,
g
β
o
)
=
e
(
g
Z
,
g
)
e\left(g^L,g^{\beta_l}\right)\cdot e\left(g^R,g^{\beta_r}\right)\cdot e\left(g^O,g^{\beta_o}\right)=e\left(g^Z,g\right)
e(gL,gβl)⋅e(gR,gβr)⋅e(gO,gβo)=e(gZ,g),即
e
(
g
,
g
)
β
l
L
+
β
r
R
+
β
o
O
=
e
(
g
,
g
)
Z
e\left(g,g\right)^{\beta_lL+\beta_rR+\beta_oO}=e\left(g,g\right)^Z
e(g,g)βlL+βrR+βoO=e(g,g)Z
可塑性问题
由于 P 在进行协议的时候知道proving 和 verification key,以单一的
l
(
x
)
l(x)
l(x)为例,那么 P 就知道了
g
α
l
,
g
β
l
,
g
s
k
g^{\alpha_l},g^{\beta_l},g^{s^k}
gαl,gβl,gsk。
这就诞生了多项式的可塑性问题
- 变量多项式的可塑性问题,就是利用常数项,导致多项式结果变化,同样可以满足 s h i f t shift shift的检验。因为知道 g s k g^{s^k} gsk,用 g s 0 = g g^{s^0} = g gs0=g,就可以计算到 g ( l a ( s ) + l d ( s ) ) × ( g ) 2 = g α ( l a ( s ) + l d ( s ) + 2 ) g^{(l_a(s)+l_d(s))} \times (g)^2 = g^{\alpha (l_a(s)+l_d(s)+2)} g(la(s)+ld(s))×(g)2=gα(la(s)+ld(s)+2)再配合知道 g α g^\alpha gα得到 g α ( l a ( s ) + l d ( s ) ) × ( g α ) 2 = g α ( l a ( s ) + l d ( s ) + 2 ) g^{\alpha (l_a(s)+l_d(s))} \times (g^{\alpha})^2 = g^{\alpha (l_a(s)+l_d(s)+2)} gα(la(s)+ld(s))×(gα)2=gα(la(s)+ld(s)+2)。这样就可以改变结果从而绕过验证。
- 变量一致性多项式的可塑性问题,和前面一样,可以使用常数配合 g β l g^{\beta_l} gβl来向多项式里添加数来绕过验证。如 g v i β l l i ( s ) × ( g β l ) 2 = g β l ( v i l i ( s ) + 2 ) g^{v_i\beta_l l_i(s)} \times (g^{\beta_l})^2 = g^{\beta_l (v_il_i(s)+2)} gviβlli(s)×(gβl)2=gβl(vili(s)+2)。
所以,不能让类似
g
α
l
,
g
β
l
g^{\alpha_l},g^{\beta_l}
gαl,gβl可见。
一种解决方案是加个掩码,也就是随机产生一个
γ
\gamma
γ,然后让它们乘以这个随机秘密,即
g
β
l
γ
,
g
β
r
γ
,
g
β
o
γ
g^{\beta_l \gamma},g^{\beta_r \gamma},g^{\beta_o \gamma}
gβlγ,gβrγ,gβoγ,那么与之对应的验证过程变为
e
(
g
L
,
g
β
l
γ
)
⋅
e
(
g
R
,
g
β
r
γ
)
⋅
e
(
g
O
,
g
β
o
γ
)
=
e
(
g
Z
,
g
γ
)
e\left(g^L,g^{\beta_l\gamma}\right)\cdot e\left(g^R,g^{\beta_r\gamma}\right)\cdot e\left(g^O,g^{\beta_o\gamma}\right)=e\left(g^Z,g^\gamma\right)
e(gL,gβlγ)⋅e(gR,gβrγ)⋅e(gO,gβoγ)=e(gZ,gγ)
BUT,如果遇到多项式都是常数的话,也就是如
l
1
(
x
)
=
1
,
r
1
(
x
)
=
0
,
o
1
(
x
)
=
0
l_1(x)=1,r_1(x)=0,o_1(x)=0
l1(x)=1,r1(x)=0,o1(x)=0,那么还是会暴露,当然前面的一致性检测已经限制了不能随意的添加常数项。
匹诺曹协议
虽然变量一致性检测很有效果,但是在验证中增加了四个 paring 操作,是开销很大的。而匹诺曹协议通过针为左右输入和输出选择了不同的生成元
g
l
=
g
ρ
l
,
g
r
=
g
ρ
r
,
g
o
=
g
ρ
o
g_l = g^{\rho_l},g_r = g^{\rho_r},g_o = g^{\rho_o}
gl=gρl,gr=gρr,go=gρo,满足
ρ
l
ρ
r
=
ρ
o
\rho_l \rho_r = \rho_o
ρlρr=ρo,然后选择用一个统一的
β
\beta
β去代替掉其他的
β
l
,
β
r
,
β
o
\beta_l,\beta_r,\beta_o
βl,βr,βo。
修改协议如下:
Setup
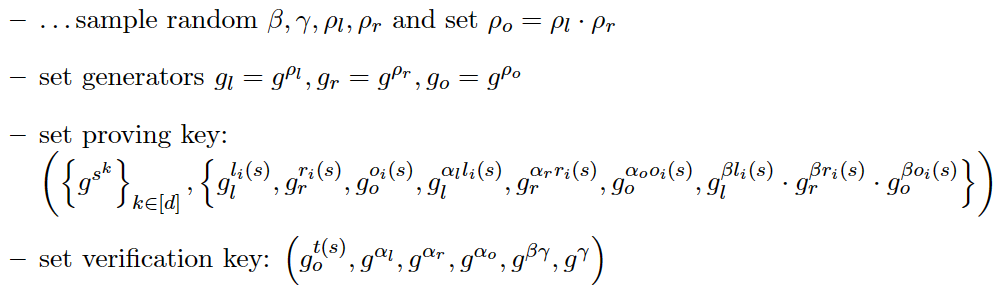
Proving
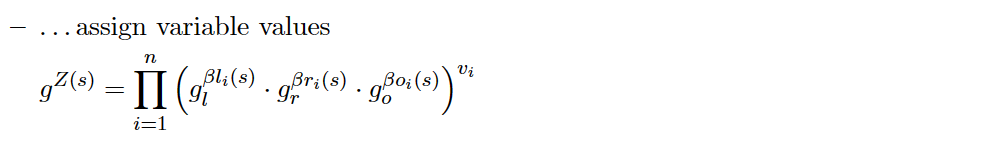
Verification

这种方式也能解决,修改多项式中的增加任意式子,绕过验证问题
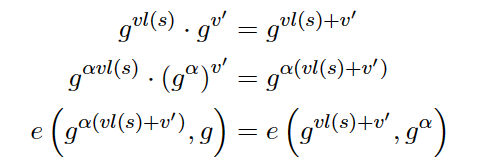
因为要更改添加,那
g
g
g必须是
ρ
l
,
ρ
r
,
ρ
o
\rho_l,\rho_r,\rho_o
ρl,ρr,ρo的倍数,原始的加密方式已经不起作用了。
同时验证的 paring 也缩小为了两次,大大减少开销。
增加零知识性
主要是 P 提供的任何确定性的证明均不能满足零知识的需求,如不能透露变量
v
v
v的具体赋值,具体的
L
(
x
)
,
R
(
x
)
,
O
(
x
)
,
h
(
x
)
L(x),R(x),O(x),h(x)
L(x),R(x),O(x),h(x)构造方式等等。所以,需要添加掩码,也就是随机
s
h
i
f
t
shift
shift
使得证明看起来和随机数没有什么区别但是能通过验证。
当然,不能单纯使用同一个,不然相同的多项式中即便加入掩码也是会暴露的,为了提高更深的安全性,需要使用多个随机数
δ
i
\delta_i
δi。类似构造如下式子
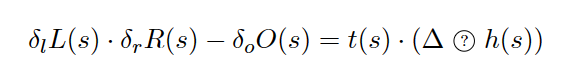
其中 Δ \Delta Δ代表平衡左右两边等式的差异值, ? ? ?代表的是运算符号即加减乘除。多项式证明就是证明上面的等式,所以我们需要找到一个合适的能够方便计算出来的差异部分去运用 paring 进行验证。
- 假设运算符号为乘法,随机选取 δ l , δ r , δ o \delta_l,\delta_r,\delta_o δl,δr,δo,得到
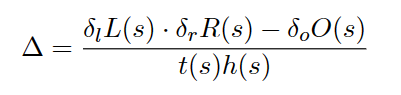
但是因为介个
δ
i
\delta_i
δi是随机的,不能绝对保证能计算出来这个
Δ
\Delta
Δ,不是一个整除的结果。
那么赋予随机数一定关系呢?假设满足
δ
l
δ
r
=
δ
o
\delta_l\delta_r=\delta_o
δlδr=δo,那么有
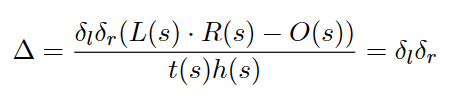
这种结构显然的违背了零知识,它会泄露
L
(
x
)
,
R
(
x
)
,
O
(
x
)
L(x),R(x),O(x)
L(x),R(x),O(x)之间的关系,如
e
(
g
δ
l
L
(
s
)
,
g
δ
r
R
(
s
)
)
=
e
(
g
δ
o
O
(
s
)
,
g
)
e(g^{\delta_lL(s)},g^{\delta_rR(s)}) = e(g^{\delta_oO(s)},g)
e(gδlL(s),gδrR(s))=e(gδoO(s),g)那么就可以确定
L
(
x
)
×
R
(
x
)
=
O
(
x
)
L(x)\times R(x)=O(x)
L(x)×R(x)=O(x)的关系了。
那么如果改成随机数加法呢?
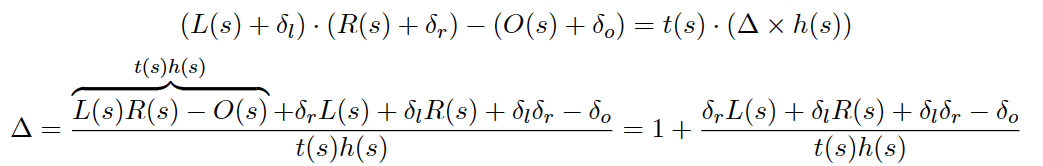
注意到,由于介个
δ
i
\delta_i
δi是随机的,所以大概率不能够整除。那么分子同时乘以一个分母
t
(
s
)
h
(
s
)
t(s)h(s)
t(s)h(s)呢?注意到前面的式子里有
Δ
×
h
(
s
)
\Delta \times h(s)
Δ×h(s),实际上是加密状态下的,也就是
g
Δ
×
h
(
s
)
g^{\Delta \times h(s)}
gΔ×h(s),但是不支持同态乘法,所以不行。即便可以,要知道
Δ
,
h
(
s
)
\Delta , h(s)
Δ,h(s)都是
d
d
d阶的多项式,乘积就是
2
d
2d
2d阶的,
g
s
i
g^{s_i}
gsi可是只有
d
d
d阶的。所以不行。
- 假设运算符号为加法
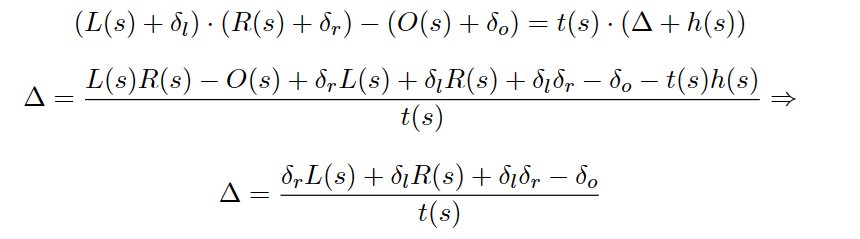
再给分子每一个
δ
\delta
δ都乘以一个
t
(
s
)
t(s)
t(s),就可以消除掉分母,
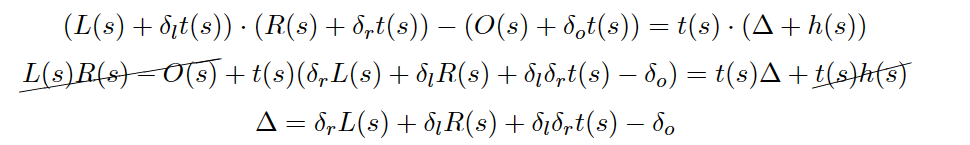
即证明式子变为
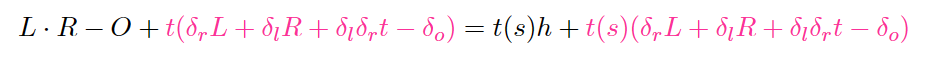
完整的ZKSNARK

注意
t
(
x
)
t(x)
t(x),基准多项式,生成元,Proving 和 Verification key都是可见的。


参考
浅谈零知识证明:背景与起源
zcash官方科普
Exploring Elliptic Curve Pairings
Quadratic Arithmetic Programs: from Zero to Hero
Why and how zk-SNARK works
ZKSNARK介绍
李威翰,张宗洋,周子博等.简洁非交互零知识证明综述[J].密码学报,2022,9(03):379-447.DOI:10.13868/j.cnki.jcr.000525.