写这个题目的原因

1、今天在看王道考研数据结构的课（虽然我要保研，但是因为这些看保研面试的时候会问，所以看一下嘞orz），看到了这个多叉树转换为二叉树的知识点。
2、上学期上编译原理课的时候老师上课也提问过这个问题，所以今天尝试着用c++的代码实现一下。

寻找提交网址

1、POJ不知道为什么，提交任何代码都一直报错
（目前时间为2023年8月30日）
然后我去了洛谷、AcWing、LeetCode、PTA都没有搜到这个题目。。。
2、无奈之下去了VJudge，最终在一个韩国的OJ上提交了这个题目，并成功AC，中间的过程也算是一波三折。
这里附上提交的网址：
Tree Grafting（韩国的OJ）
Tree Grafting（POJ）

题目解决思路

题目输入有多行，每行代表一个建树的过程，由d或者u组成。d表示往下新建节点，u表示往上走到当前节点的父亲，这样走下来就得到了一个多叉树。
最终让求解：
1、多叉树的深度，即dep1
2、转换后的二叉树的深度，即dpe2

对于dep1，通过观察输入的字符串可以发现，每一个d即为往下新建一个节点，这里我们可以使用“前缀和”的思想，新建一个变量t，初始值为0，遇到d加一，遇到u减一，在这个过程中最大的t即为要求解的dep1

比如对于题目给出的第一个输入，初始t=0
dudduduudu，对应的t为
1012121010，所以多叉树的深度为2，即为求解的第一个变量

对于dep2的求解，我们可以对所有的节点设置唯一的一个变量标记（用int就可以实现），然后进行反向建边，用一个一维的数组就可以存储所有的二叉树

当然看到这里有人可能会问，为什么不正向建边？
答：因为这是一个多叉树，一个节点可能有多个儿子，题目的最多节点为10000，那么如果正向建边的话，至少得10000^2大小的数组，可能会爆内存！

这样反向建边之后，我们相当于已经存储了每一个节点的父亲，那么接下来就是很常见的多叉树转换为二叉树的思路了
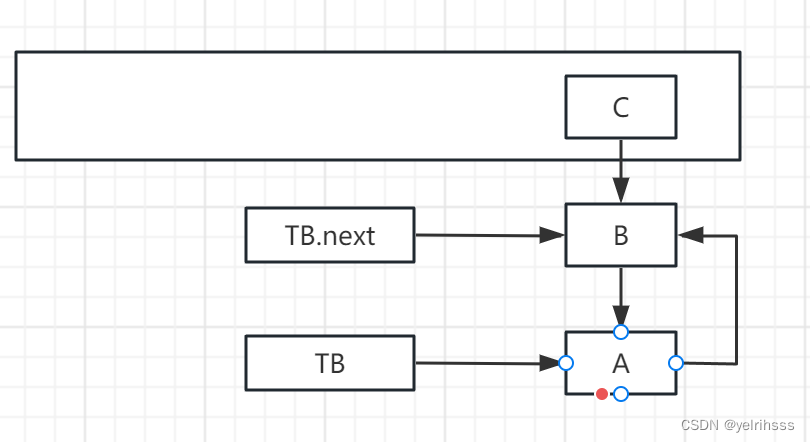
我们依次遍历所有节点，对于当前节点，如果

1、如果它父亲的左子为空：
那么直接把当前节点作为它父亲的左子
2、如果它父亲的左子不为空：
那么找它父亲左子的最右边的儿子（在这里我们定义为temp），把当前节点作为temp的右子

上面这个点如果不明白，可以百度搜索一下【多叉树怎么转换为二叉树？】会有比较详细的解释

更多细节和注释见代码

AC代码

#include <stdio.h>
#include <cstring>
#include <iostream>
using namespace std;
#define ll long long
#define sf(x) scanf("%d", &x);
#define de(x) cout << x << " ";
#define Pu puts("");
const int N = 2e4 + 9;  // 注意这里，题目中说节点最多为1e4，但是字符串长度最多为2e4
int n, m, ans;
int dep1, dep2;  // 求解的变量
char s[N];       // 输入的字符串
int fa[N];       // 记录每个节点的父亲
struct E {
    int dep;  // 存储二叉树的数据结构
    int l, r;
} e[N];
int main() {
    int now;    // 代表当前所处的节点位置
    int count;  // 代表当前新建的节点标号

    int depTmp;  // 统计多叉树的深度

    int T = 0;
    while (scanf("%s", s)) {
        if (s[0] == '#')
            break;
        T++;

        n = strlen(s);
        for (int i = 0; i < n + 1; i++) {
            fa[i] = -1;  // 所有点标记为没有父亲

            e[i].l = e[i].r = -1;
        }
        now = 0;    // 代表当前所处的位置
        count = 0;  // 代表当前新建的节点标号
        depTmp = dep1 = 0;
        for (int i = 0; i < n; i++) {
            if (s[i] == 'd') {
                count++;
                fa[count] = now;  // 向下，反向建边
                now = count;

                depTmp++;  // 进行深度统计
                if (depTmp > dep1)
                    dep1 = depTmp;
            } else if (s[i] == 'u') {
                now = fa[now];  // 向上

                depTmp--;
            }
        }
        e[0].dep = 0;
        dep2 = 0;
        for (int i = 1; i <= count; i++) {
            if (e[fa[i]].l == -1) {
                e[fa[i]].l = i;  // 如果此时父亲节点没有左子，则当前节点作为左子

                e[i].dep = e[fa[i]].dep + 1;
                if (e[i].dep > dep2)  // 深度更新
                    dep2 = e[i].dep;
            } else {  // 如果已经有了左子
                int k = e[fa[i]].l;
                while (e[k].r != -1) {
                    k = e[k].r;  // 则找左子的最右孩子
                }
                e[k].r = i;  // 新的右孩子
                e[i].dep = e[k].dep + 1;
                if (e[i].dep > dep2)  // 深度更新
                    dep2 = e[i].dep;
            }
        }
        printf("Tree %d: %d => %d\n", T, dep1, dep2);
    }
    return 0;
}