微信公众号上线,搜索公众号小灰灰的FPGA,关注可获取相关源码,定期更新有关FPGA的项目以及开源项目源码,包括但不限于各类检测芯片驱动、低速接口驱动、高速接口驱动、数据信号处理、图像处理以及AXI总线等

10、确知信号的时域性质主要包括自相关函数和互相关函数
(1)能量信号的自相关函数,公式为

自相关函数反映了一个信号与延迟τ后的同一个信号的相关程度。
当τ=0是,能量信号的自相关函数R(0)也就是该信号的能量E,即为
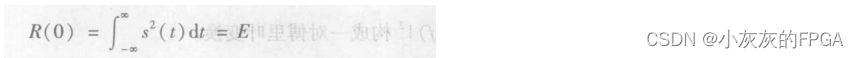
(2)能量信号的自相关函数与能量谱密度之间的关系
能量信号的自相关函数的傅里叶变换就是能量谱密度;能量信号的能量谱密度的逆傅里叶变换就是能量信号的自相关函数
推导过程如下:
能量谱密度公式:

能量信号为s(t),将其傅里叶变化S(f)称为频谱密度,用公式表示为:

对能量信号的自相关函数进行傅里叶变换:
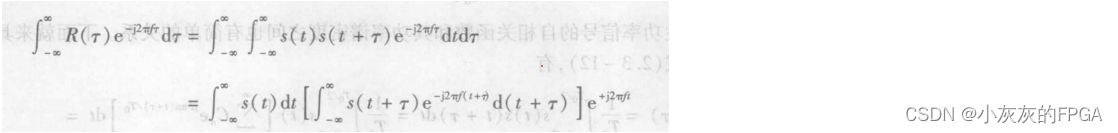
令t`=t+τ,则
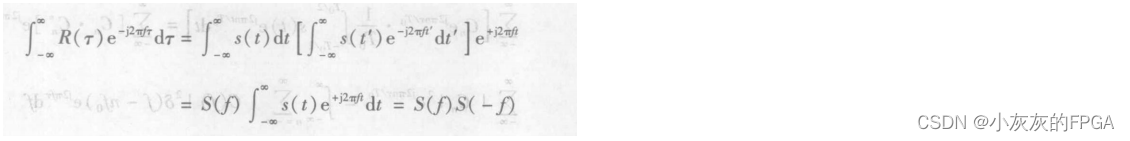
令S(f)=A(f)+jB(f),则S(-f)=A(f)-jB(f),带入可得:

由此可知R(τ)与|S(f)|^2构成一对傅里叶变换
(3)功率信号的自相关函数,公式为:

当τ=0时,功率信号的自相关函数R(0)等于信号的平均功率P,公式

(4)周期性功率信号的自相关函数和功率谱密度之间关系
周期性功率信号的自相关函数和功率谱密度P是傅里叶变换关系,R(τ)的傅里叶变换是功率谱密度,P(f)的逆傅里叶变换是R(τ)
推导过程如下:
平均功率P公式:

功率谱密度P(f)公式:

对周期性功率信号,自相关函数R(τ)
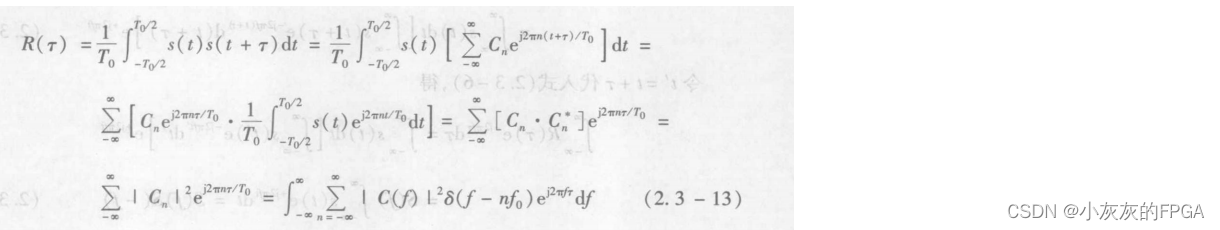
由此可得出:

(5)两个能量信号s1(t)和s2(t)的互相关函数,公式如下:

互相关函数反映了一个信号和延迟τ后的另一个信号间相关程度,互相关函数和两个信号相乘的前后次序有关,即:

推导过程:
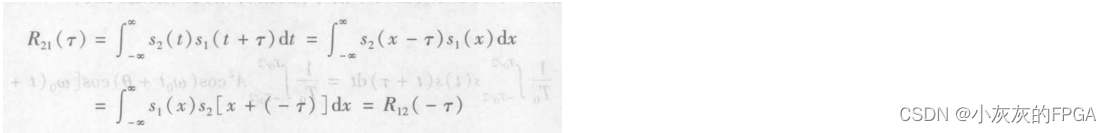
(6)互相关函数和信号能量密度的关系
R12(τ)是S12(f)的逆傅里叶变换,S12(f)是R12(τ)的傅里叶变换
推导过程:
能量信号为s(t),将其傅里叶变化S(f)称为频谱密度,用公式表示为:

将S2(t+τ)带入可得:
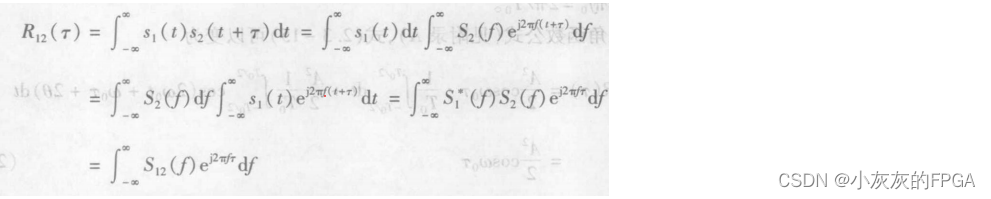
上式中S12(f)为互能量密度
(7)两个功率信号s1(t)和s2(t)的互相关函数,公式如下:
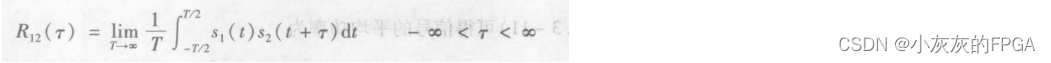
互相关函数反映了一个信号和延迟τ后的另一个信号间相关程度,互相关函数和两个信号相乘的前后次序有关,即:

(6)互相关函数和功率谱的关系
周期性功率信号的互功率谱C12是其互相关函数R12(τ)的傅里叶系数

C12称为信号的互功率谱

通信原理板块——基础知识(四)
news2026/2/13 12:17:31
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/949495.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
自然语言处理(NLP)是什么?
NLP(自然语言处理) 和 Phoebe Liu 的简介
您有没有和聊天机器人互动过?或者您是否向虚拟助手,例如 Siri、Alexa 或您车上的车载娱乐系统发出过某些请求?您使用过在线翻译吗?我们大多数人都曾与这些人工智能 (AI) 互动过ÿ…
校园用电安全管理系统可以识别违规电器吗
校园用电安全管理系统是处理恶意用电问题有效手段之一,系统具有实时监测、异常预警、监测设备运行状态、远程控制用电等功能,可以从根本上管理学校用电量,制定合理的用电计划,限制用电成本,避免各种恶意用电行为&#…
windows环境搭建ELK
目录
资源下载(8.9.1)
ES安装、注册、使用
Kibana安装、注册、使用
Logstash安装、注册、使用
Filebeat安装、使用(如果只有一个数据流,则不需要使用filebeat,直接上logstash即可) 资源下载࿰…
关于商品活动的H5页面技术总结
背景
在单个html文件里面使用vue3、jquery等其他第三方js库,实现规定的页面效果,其中主要功能是从商品json数据中读取数据,然后可以通过搜索框、下拉框、左侧菜单来筛选商户信息。
页面布局 技术要点:
1、通过路由来进行页面布…
Django实现音乐网站 ⒁
使用Python Django框架制作一个音乐网站, 本篇主要是歌手页-全部歌手页功能开发。 目录
分出首页样式内容
创建首页样式文件
首页引入样式文件
全部歌手列表
创建路由
显示视图
引入分页实现库
视图方法
创建歌手首页
增加歌手跳转
导航条改活
首页增加…
EMC 性能优异的ISO7761QDBQQ1、ISO7762QDWQ1、ISO7741QDWWQ1、ISO7710QDRQ1汽车类数字隔离器
一、EMC 性能优异的 ISO776x-Q1 高速、增强型六通道数字隔离器
ISO776x-Q1 器件是高性能六通道数字隔离器,可提供符合 UL 1577 的 5000VRMS(DW 封装)和 3000VRMS(DBQ 封装)隔离额定值。该系列器件还通过了VDE、CSA、T…
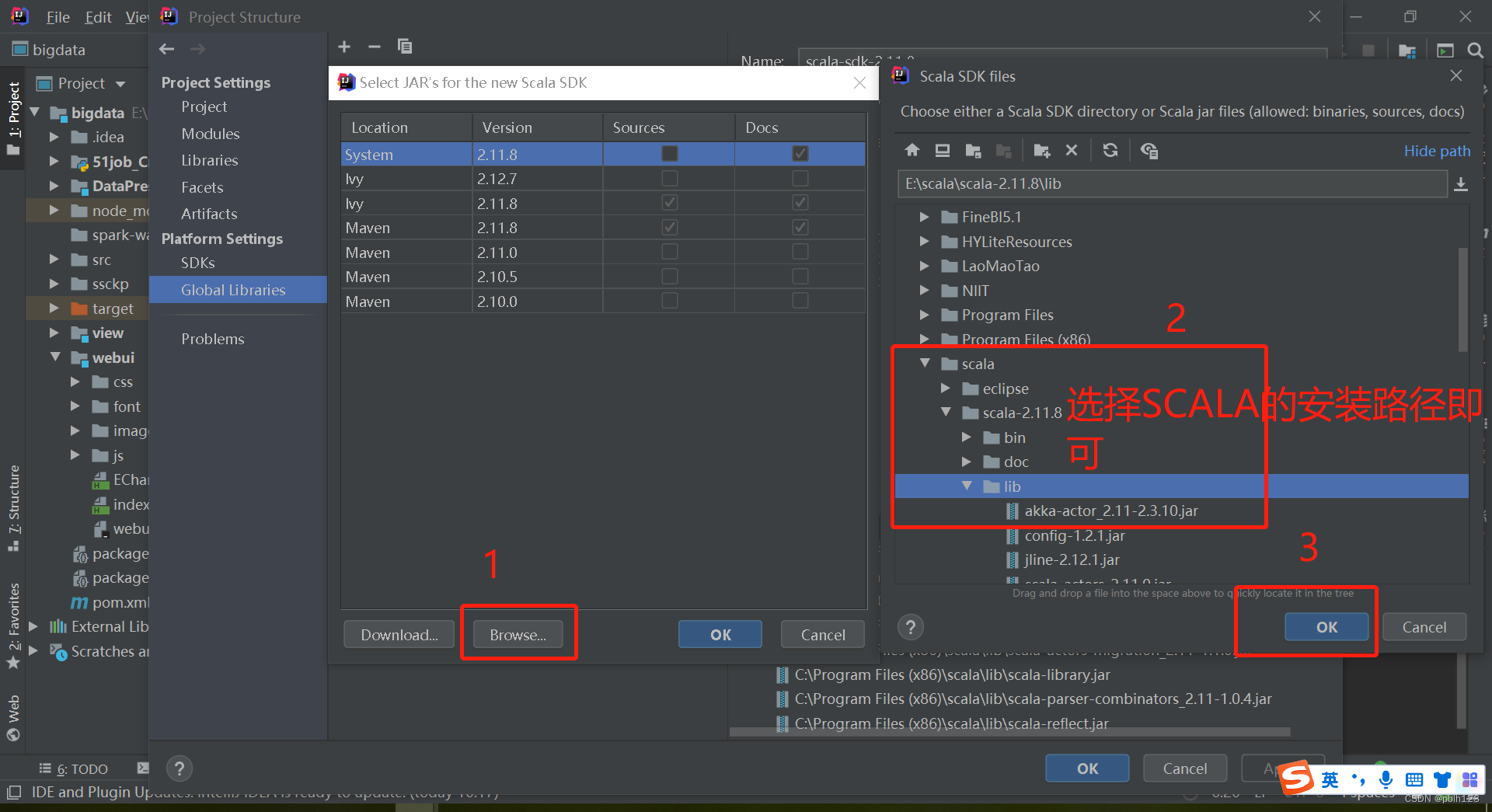
2023_Spark_实验二:IDEA安装及配置
一、下载安装包
链接:百度网盘 请输入提取码 所在文件夹:大数据必备工具--》开发工具(前端后端)--》后端
下载文件名称:ideaIU-2019.2.3.exe
(喜欢新版本也可安装新版本,新旧版本会存在部分差异)
IDEA …
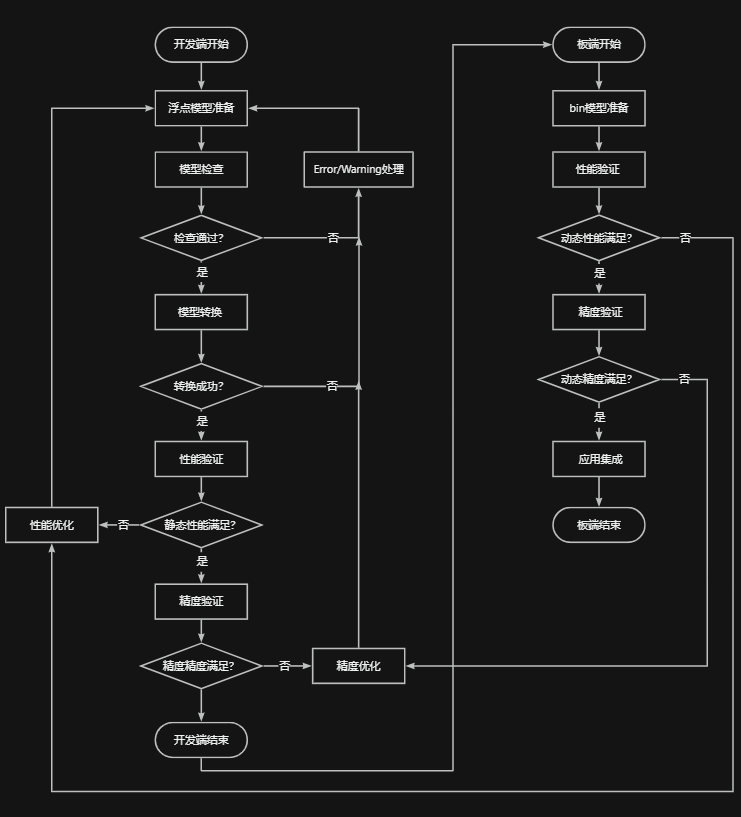
极智AI | 地平线天工开物工具链部署流程详解
欢迎关注我的公众号 [极智视界],获取我的更多经验分享
大家好,我是极智视界,本文来介绍一下 地平线天工开物工具链部署流程详解。 邀您加入我的知识星球「极智视界」,星球内有超多好玩的项目实战源码下载,链接:https://t.zsxq.com/0aiNxERDq 地平线天工开物工具链从完备…
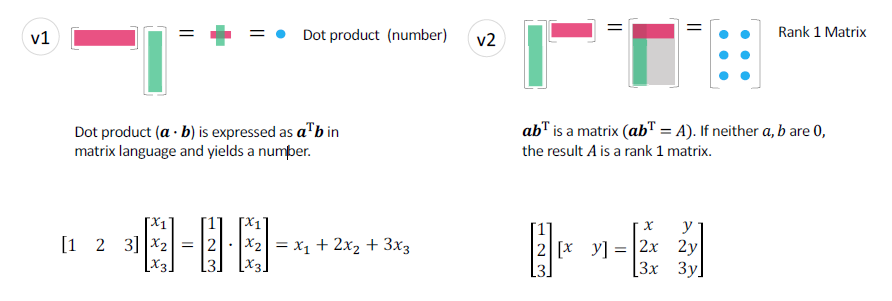
【AI】数学基础——线代(向量部分)
参考: kenjihiranabe——The-Art-of-Linear-Algebra-zh-CN 详细计算方法与理论:见 矩阵论 线性代数的本质在于将具体事物抽象为数学对象,并描述其静态和动态特性 最基本的概念是 set 集合的定义是由某些具有某些共性的对象汇总成的集体。 将这…
go语言 go mod生成
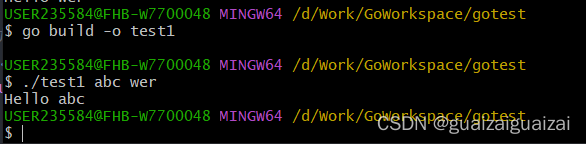
1. go hello world
创建文件夹gotest,在其中创建test1.go文件,并写入
package mainimport ("fmt"
)func main() {fmt.Println("hello world")
} 运行命令 go run test1.go 可以看到输出hello world 2. cli 命令行的使用
代码如下…
Git 速查表:中级用户必备的 12 个 Git 命令
本文译自:Git Cheat Sheet: 12 Essential Git Commands For Intermediate Users,原文链接:https://initialcommit.com/blog/git-cheat-sheet-intermediate 本系列共有三篇文章,本文是第二篇:
Git Cheat Sheet: 12 Ess…
了解 HarmonyOS
引言
在开始 HarmonyOS 开发之前,了解其背景、特点和架构是非常重要的。本章将为你提供一个全面的 HarmonyOS 概览。
目录 什么是 HarmonyOS HarmonyOS 的发展历程 HarmonyOS 的特点 HarmonyOS 的架构 HarmonyOS 与其他操作系统的比较
1. 什么是 HarmonyOS …
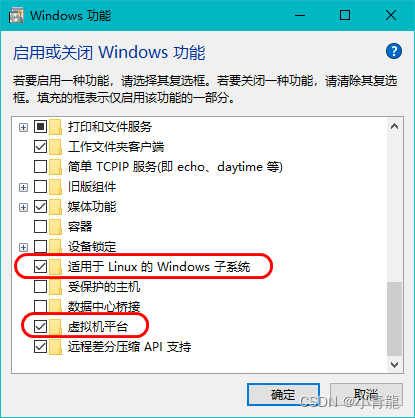
如何在WSL上导入任何Linux发行版
文章目录 一、准备1. 开启WSL相关功能2. 升级WSL3. 设置默认的wsl版本 二、通过 Microsoft Store 安装 Linux1. 查看 Microsoft Store 有哪些可安装的 Linux 发行版2. 安装 Linux 发行版3. 查看已安装的 Linux 发行版4. 启动Linux发行版 三、通过Linux发行商提供的tar文件安装1…
[PyTorch][chapter 53][Auto Encoder 实战]
前言: 结合手写数字识别的例子,实现以下AutoEncoder ae.py: 实现autoEncoder 网络 main.py: 加载手写数字数据集,以及训练,验证,测试网络。
左图:原图像
右图:重构图像 ----main----- 每轮训…
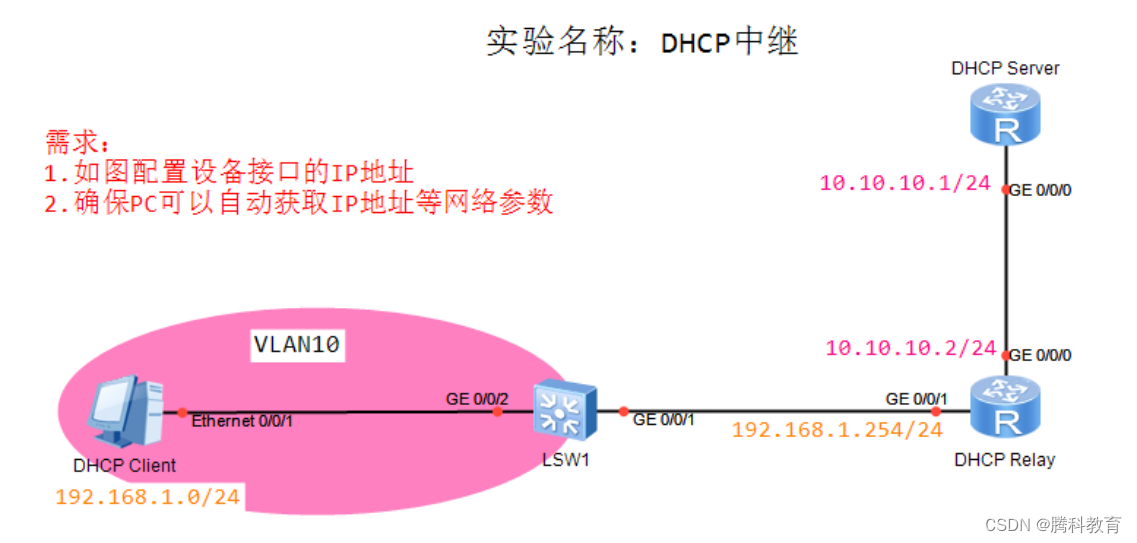
DHCP 服务器部署
| DHCP - - > Dynamic Host Configuration Protocol 动态主机配置协议
背景
任何一个需要上网的设备,都必须得有IP地址,子网掩码,网关,等等网络参数。比如:手机,电脑,智能手表,…
【SpringBoot学习笔记】02.静态资源与首页订制
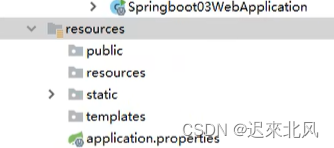
静态资源
Spring Boot 通过 MVC 的自动配置类 WebMvcAutoConfiguration 为这些 WebJars 前端资源提供了默认映射规则,部分源码如下。 jar包: JAR 文件就是 Java Archive File,顾名思意,它的应用是与 Java 息息相关的,…
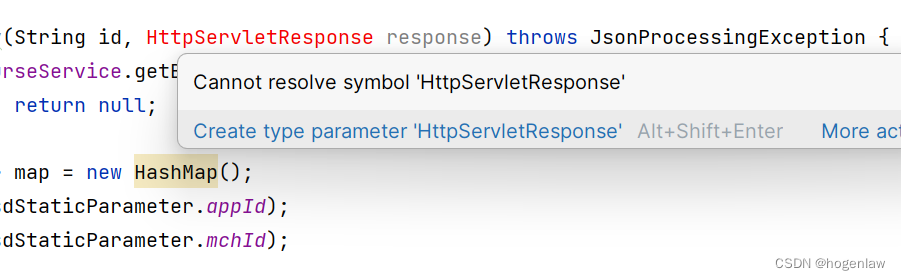
IDEA 报 Cannot resolve symbol ‘HttpServletResponse‘ 解决
springboot2版本换成springboot3之后,代码这里突然报红了,
首先要淡定,把原先Import的引入删掉,重新引入试试呢,是不是很简单哈哈。
原来,springboot3的路径是: import jakarta.servlet.http…
Docker之私有仓库 RegistryHarbor
目录 一、Docker私有仓库(Registry)
1.1 Registry的介绍 二、搭建本地私有仓库
2.1首先下载 registry 镜像
2.2在 daemon.json 文件中添加私有镜像仓库地址 2.3运行 registry 容器
2.4Docker容器的重启策略
2.5为镜像打标签
2.6上传到私有仓库
2…






![[PyTorch][chapter 53][Auto Encoder 实战]](https://img-blog.csdnimg.cn/1f4a5174a09a4374a2a8935c457ec996.png)