一、说明

二、技术背景
位置编码用于为序列中的每个标记或单词提供相对位置。阅读句子时,每个单词都依赖于它周围的单词。例如,某些单词在不同的上下文中具有不同的含义,因此模型应该能够理解这些变体以及每个单词所依赖的上下文。一个例子是“树干”。在一个例子中,它可以用来指大象用它的鼻子喝水。在另一种情况下,它可能是指树干被照明击中。
由于该模型使用长度d_model的嵌入向量来表示每个单词,因此任何位置编码都必须兼容。使用整数似乎很自然,第一个令牌接收 0,第二个令牌接收 1,依此类推。但是,这个数字会迅速增长,并且不容易添加到嵌入矩阵中。相反,为每个位置创建一个位置编码向量,这意味着可以创建一个位置编码矩阵来表示单词可以采取的所有可能位置。
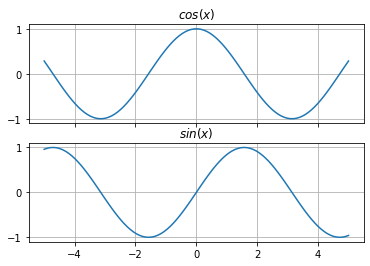
为了确保每个位置都有唯一的表示,“注意力是你所需要的一切”的作者使用正弦和余弦函数为序列中的每个位置生成一个唯一的向量。虽然这看起来很奇怪,但它有用有几个原因。首先,正弦和余弦的输出在 [-1, 1] 中,归一化。它不会像整数那样增长到无法管理的大小。其次,无需进行额外的培训,因为每个职位都会生成独特的表示形式。
用于生成独特编码的方程看起来令人生畏,但它们只是正弦和余弦的修改版本。嵌入中的最大位置数或向量将由 L 表示:

这实质上是说,对于每个位置编码向量,对于每两个元素,将偶数元素设置为等于 PE(k,2i),并将奇数元素设置为等于 PE(k, 2i+1)。然后,重复直到向量中有d_model个元素。
每个编码向量具有与嵌入向量相同的维度(d_model)。这允许对它们求和。k 表示位置,从 0 开始到 L-1。i 可以设置为的最大数字是 d_model除以 2,因为方程对嵌入中的每个元素交替。n可以设置为任何值,但原始论文建议10,000。在下图中,以下参数用于计算 6 标记序列的位置编码向量:
- n = 10,000
- L = 6
- d_model = 4
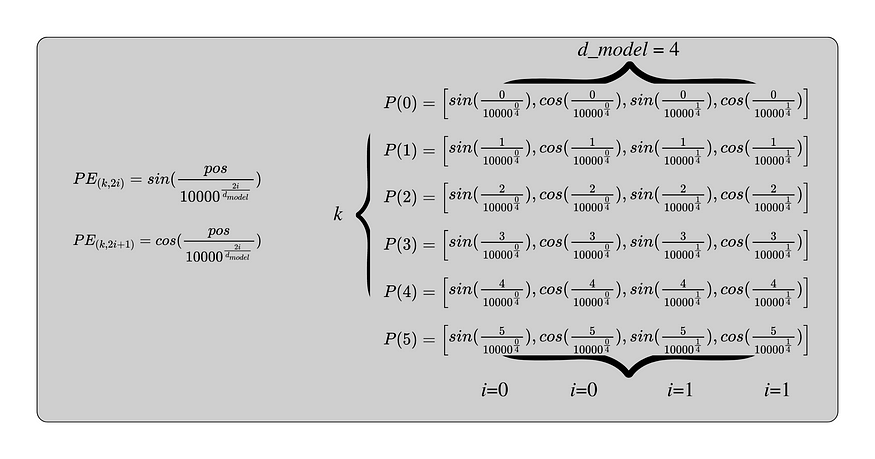
此图显示了最大值 i 如何设置为 1,正弦和余弦都使用它。k 随嵌入矩阵中的每一行而变化,从 0 开始到 5,这是最大长度 6。每个向量有 d_model = 4 个元素。
三、基本实现

要了解这些独特的位置编码向量如何与嵌入向量一起工作,最好使用嵌入层文章中的示例。
此实现将直接基于上一篇文章中的实现构建。下面的输出嵌入了三个序列,d_model为 4。
# set the output to 2 decimal places without scientific notation
torch.set_printoptions(precision=2, sci_mode=False)
# tokenize the sequences
tokenized_sequences = [tokenize(seq) for seq in sequences]
# index the sequences
indexed_sequences = [[stoi[word] for word in seq] for seq in tokenized_sequences]
# convert the sequences to a tensor
tensor_sequences = torch.tensor(indexed_sequences).long()
# vocab size
vocab_size = len(stoi)
# embedding dimensions
d_model = 4
# create the embeddings
lut = nn.Embedding(vocab_size, d_model) # look-up table (lut)
# embed the sequence
embeddings = lut(tensor_sequences)
embeddingstensor([[[-0.27, -0.82, 0.33, 1.39],
[ 1.72, -0.63, -1.13, 0.10],
[-0.23, -0.07, -0.28, 1.17],
[ 0.61, 1.46, 1.21, 0.84],
[-2.05, 1.77, 1.51, -0.21],
[ 0.86, -1.81, 0.55, 0.98]],
[[ 0.06, -0.34, 2.08, -1.24],
[ 1.44, -0.64, 0.78, -1.10],
[ 1.78, 1.22, 1.12, -2.35],
[-0.48, -0.40, 1.73, 0.54],
[ 1.28, -0.18, 0.52, 2.10],
[ 0.34, 0.62, -0.45, -0.64]],
[[-0.22, -0.66, -1.00, -0.04],
[-0.23, -0.07, -0.28, 1.17],
[ 1.44, -0.64, 0.78, -1.10],
[ 1.78, 1.22, 1.12, -2.35],
[-0.48, -0.40, 1.73, 0.54],
[ 0.70, -1.35, 0.15, -1.44]]], grad_fn=<EmbeddingBackward0>)下一步是通过位置编码对每个序列中每个单词的位置进行编码。下面的函数遵循上面的定义。唯一值得一提的变化是 L 被标记为max_length。它通常设置为千中的极大值,以确保几乎每个序列都可以正确编码。这确保了相同的位置编码矩阵可以用于不同长度的序列。在添加之前可以将其切成适当的长度。
def gen_pe(max_length, d_model, n):
# generate an empty matrix for the positional encodings (pe)
pe = np.zeros(max_length*d_model).reshape(max_length, d_model)
# for each position
for k in np.arange(max_length):
# for each dimension
for i in np.arange(d_model//2):
# calculate the internal value for sin and cos
theta = k / (n ** ((2*i)/d_model))
# even dims: sin
pe[k, 2*i] = math.sin(theta)
# odd dims: cos
pe[k, 2*i+1] = math.cos(theta)
return pe
# maximum sequence length
max_length = 10
n = 100
encodings = gen_pe(max_length, d_model, n)编码的输出包含 10 个位置编码向量。
array([[ 0. , 1. , 0. , 1. ],
[ 0.8415, 0.5403, 0.0998, 0.995 ],
[ 0.9093, -0.4161, 0.1987, 0.9801],
[ 0.1411, -0.99 , 0.2955, 0.9553],
[-0.7568, -0.6536, 0.3894, 0.9211],
[-0.9589, 0.2837, 0.4794, 0.8776],
[-0.2794, 0.9602, 0.5646, 0.8253],
[ 0.657 , 0.7539, 0.6442, 0.7648],
[ 0.9894, -0.1455, 0.7174, 0.6967],
[ 0.4121, -0.9111, 0.7833, 0.6216]])如前所述,max_length设置为 10。虽然这超出了要求,但它确保如果另一个序列的长度为 7、8、9 或 10,则可以使用相同的位置编码矩阵。它只需要被切成适当的长度。下面,嵌入的seq_length为 <>,因此可以相应地对编码进行切片。
# select the first six tokens
seq_length = embeddings.shape[1]
encodings[:seq_length]tensor([[ 0.00, 1.00, 0.00, 1.00],
[ 0.84, 0.54, 0.10, 1.00],
[ 0.91, -0.42, 0.20, 0.98],
[ 0.14, -0.99, 0.30, 0.96],
[-0.76, -0.65, 0.39, 0.92],
[-0.96, 0.28, 0.48, 0.88]])由于所有三个序列的序列长度相同,因此只需要一个位置编码矩阵,并且可以使用 PyTorch 在所有三个序列上广播。此示例中的嵌入批处理的形状为 (3, 6, 4),位置编码在切片为 (10, 4) 之前形状为 (6, 4)。然后广播该矩阵以创建图像中看到的(3,6,4)编码矩阵。有关广播的更多信息,请阅读广播简单简介。
这允许添加两个矩阵而不会出现任何问题。
embedded_sequence + encodings[:seq_length] # encodings[:6]将位置编码添加到嵌入时,输出与部分开头的图像相同。
tensor([[[-0.27, 0.18, 0.33, 2.39],
[ 2.57, -0.09, -1.03, 1.09],
[ 0.68, -0.49, -0.08, 2.15],
[ 0.75, 0.47, 1.50, 1.80],
[-2.80, 1.12, 1.90, 0.71],
[-0.10, -1.53, 1.03, 1.86]],
[[ 0.06, 0.66, 2.08, -0.24],
[ 2.28, -0.10, 0.88, -0.10],
[ 2.69, 0.80, 1.32, -1.37],
[-0.34, -1.39, 2.03, 1.50],
[ 0.52, -0.83, 0.91, 3.02],
[-0.62, 0.90, 0.03, 0.23]],
[[-0.22, 0.34, -1.00, 0.96],
[ 0.61, 0.47, -0.18, 2.16],
[ 2.35, -1.06, 0.98, -0.12],
[ 1.92, 0.23, 1.41, -1.40],
[-1.24, -1.06, 2.12, 1.46],
[-0.26, -1.06, 0.63, -0.56]]], grad_fn=<AddBackward0>)此输出将传递到模型的下一层,即下一篇文章将介绍的多头注意力。
但是,由于此基本实现使用嵌套循环,因此效率不高,尤其是在使用较大的 d_model 和 max_length 值时。相反,可以使用更以 PyTorch 为中心的方法。
四、修改 PyTorch 的位置编码公式

图片来源:Chili Math
为了利用 PyTorch 的功能,需要使用对数规则修改原始方程,特别是除数。
除数为:

为了修改除数,通过取其指数将 n 带入分子中。然后,使用规则 7 将整个方程提高为 e 的指数。然后,使用规则 3 将指数拉出日志。然后简化以获得结果。
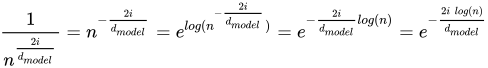
这很重要,因为它可用于一次生成位置编码的所有除数。下面很明显,4 维嵌入只需要两个除数,因为除数每 2i 才会变化一次,其中 i 是维度。这在每个位置重复:

由于只有 i 可以设置为的最大数字d_model除以 2,因此可以计算一次项:
d_model = 4
n = 100
div_term = torch.exp(torch.arange(0, d_model, 2) * -(math.log(n) / d_model))这个简短的代码片段可用于生成所需的所有除数。对于此示例,d_model设置为 4,n 设置为 100。输出是两个除数:
tensor([1.0000, 0.1000])从这里,可以利用 PyTorch 的索引功能,用几行代码创建整个位置编码矩阵。下一步是生成从 k 到 L-1 的每个位置。
max_length = 10
# generate the positions into a column matrix
k = torch.arange(0, max_length).unsqueeze(1) tensor([[0],
[1],
[2],
[3],
[4],
[5],
[6],
[7],
[8],
[9]])使用位置和除数,可以轻松计算正弦和余弦函数的内部。

通过将 k 和 div_term相乘,可以计算每个位置的输入。PyTorch 将自动广播矩阵以允许乘法。请注意,这是 Hadamard 乘积而不是矩阵乘法,因为相应的元素将相互乘法:

k*div_term此计算的输出可以在上图中看到。剩下要做的就是将输入插入 cos 和 sin 函数,并将它们适当地保存在矩阵中。
这可以通过创建适当大小的空矩阵来开始:
# generate an empty tensor
pe = torch.zeros(max_length, d_model)tensor([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])现在,偶数列是罪恶的,可以用 pe[:, 0::2] 选择。这告诉 PyTorch 选择每一行和每一列偶数列。对于奇数列也可以这样做,它们是 cos: pe[:, 1::2]。再一次,这告诉 PyTorch 选择每一行和每一奇数列。由于 k*div_term 的结果中存储了所有必要的输入,因此可用于计算每个奇数和偶数列。
# set the odd values (columns 1 and 3)
pe[:, 0::2] = torch.sin(k * div_term)
# set the even values (columns 2 and 4)
pe[:, 1::2] = torch.cos(k * div_term)
# add a dimension for broadcasting across sequences: optional
pe = pe.unsqueeze(0) tensor([[[ 0.00, 1.00, 0.00, 1.00],
[ 0.84, 0.54, 0.10, 1.00],
[ 0.91, -0.42, 0.20, 0.98],
[ 0.14, -0.99, 0.30, 0.96],
[-0.76, -0.65, 0.39, 0.92],
[-0.96, 0.28, 0.48, 0.88],
[-0.28, 0.96, 0.56, 0.83],
[ 0.66, 0.75, 0.64, 0.76],
[ 0.99, -0.15, 0.72, 0.70],
[ 0.41, -0.91, 0.78, 0.62]]])这些值与使用嵌套的 for 循环获取的值相同。回顾一下,以下是所有代码:
max_length = 10
d_model = 4
n = 100
def gen_pe(max_length, d_model, n):
# calculate the div_term
div_term = torch.exp(torch.arange(0, d_model, 2) * -(math.log(n) / d_model))
# generate the positions into a column matrix
k = torch.arange(0, max_length).unsqueeze(1)
# generate an empty tensor
pe = torch.zeros(max_length, d_model)
# set the even values
pe[:, 0::2] = torch.sin(k * div_term)
# set the odd values
pe[:, 1::2] = torch.cos(k * div_term)
# add a dimension
pe = pe.unsqueeze(0)
# the output has a shape of (1, max_length, d_model)
return pe
gen_pe(max_length, d_model, n) 虽然它更复杂,但这是 PyTorch 使用的实现,因为它增强了机器学习的性能。
五、变压器中的位置编码
现在所有的艰苦工作都已经完成,实施很简单。它源自注释转换器和PyTorch。请注意,n 的默认值为 10,000,默认max_length为 5,000。
此实现还包含 dropout,它以给定的概率 p 随机清零其输入的某些元素。这有助于正则化并防止神经元共同适应(过度依赖彼此)。输出也按¹⁄₍₁_p₎的系数进行缩放。而不是在本文中深入讨论它。有关详细信息,请参阅有关辍学层的文章。在转向变压器模型的其余部分之前,最好现在就熟悉它,因为它几乎位于其他每一层中。
class PositionalEncoding(nn.Module):
def __init__(self, d_model: int, dropout: float = 0.1, max_length: int = 5000):
"""
Args:
d_model: dimension of embeddings
dropout: randomly zeroes-out some of the input
max_length: max sequence length
"""
# inherit from Module
super().__init__()
# initialize dropout
self.dropout = nn.Dropout(p=dropout)
# create tensor of 0s
pe = torch.zeros(max_length, d_model)
# create position column
k = torch.arange(0, max_length).unsqueeze(1)
# calc divisor for positional encoding
div_term = torch.exp(
torch.arange(0, d_model, 2) * -(math.log(10000.0) / d_model)
)
# calc sine on even indices
pe[:, 0::2] = torch.sin(k * div_term)
# calc cosine on odd indices
pe[:, 1::2] = torch.cos(k * div_term)
# add dimension
pe = pe.unsqueeze(0)
# buffers are saved in state_dict but not trained by the optimizer
self.register_buffer("pe", pe)
def forward(self, x: Tensor):
"""
Args:
x: embeddings (batch_size, seq_length, d_model)
Returns:
embeddings + positional encodings (batch_size, seq_length, d_model)
"""
# add positional encoding to the embeddings
x = x + self.pe[:, : x.size(1)].requires_grad_(False)
# perform dropout
return self.dropout(x)前向传递
要执行正向传递,可以使用与之前相同的嵌入式序列。
embeddingstensor([[[-0.27, -0.82, 0.33, 1.39],
[ 1.72, -0.63, -1.13, 0.10],
[-0.23, -0.07, -0.28, 1.17],
[ 0.61, 1.46, 1.21, 0.84],
[-2.05, 1.77, 1.51, -0.21],
[ 0.86, -1.81, 0.55, 0.98]],
[[ 0.06, -0.34, 2.08, -1.24],
[ 1.44, -0.64, 0.78, -1.10],
[ 1.78, 1.22, 1.12, -2.35],
[-0.48, -0.40, 1.73, 0.54],
[ 1.28, -0.18, 0.52, 2.10],
[ 0.34, 0.62, -0.45, -0.64]],
[[-0.22, -0.66, -1.00, -0.04],
[-0.23, -0.07, -0.28, 1.17],
[ 1.44, -0.64, 0.78, -1.10],
[ 1.78, 1.22, 1.12, -2.35],
[-0.48, -0.40, 1.73, 0.54],
[ 0.70, -1.35, 0.15, -1.44]]], grad_fn=<EmbeddingBackward0>)嵌入序列后,可以创建位置编码矩阵。dropout 设置为 0.0 以便轻松查看嵌入和位置编码之间的相加。这些值与从头开始实现不同,因为 n 的默认值为 10,000 而不是 100。
d_model = 4
max_length = 10
dropout = 0.0
# create the positional encoding matrix
pe = PositionalEncoding(d_model, dropout, max_length)
# preview the values
pe.state_dict()OrderedDict([('pe',
tensor([[[ 0.00, 1.00, 0.00, 1.00],
[ 0.84, 0.54, 0.01, 1.00],
[ 0.91, -0.42, 0.02, 1.00],
[ 0.14, -0.99, 0.03, 1.00],
[-0.76, -0.65, 0.04, 1.00],
[-0.96, 0.28, 0.05, 1.00],
[-0.28, 0.96, 0.06, 1.00],
[ 0.66, 0.75, 0.07, 1.00],
[ 0.99, -0.15, 0.08, 1.00],
[ 0.41, -0.91, 0.09, 1.00]]]))])在添加它们之前,序列的形状为 (batch_size、seq_length、d_model),即 (3, 6, 4)。位置编码在切片和广播后具有相同的大小,因此前向传递的输出大小为 (batch_size、seq_length、d_model),仍然是 (3, 6, 4)。这表示嵌入在 3 维空间中的 6 个序列,每个序列 4 个令牌,带有位置编码以指示它们在序列中的位置。
pe(embeddings) tensor([[[-0.27, 0.18, 0.33, 2.39],
[ 2.57, -0.09, -1.12, 1.10],
[ 0.68, -0.49, -0.26, 2.17],
[ 0.75, 0.47, 1.24, 1.84],
[-2.80, 1.12, 1.55, 0.79],
[-0.10, -1.53, 0.60, 1.98]],
[[ 0.06, 0.66, 2.08, -0.24],
[ 2.28, -0.10, 0.79, -0.10],
[ 2.69, 0.80, 1.14, -1.35],
[-0.34, -1.39, 1.76, 1.54],
[ 0.52, -0.83, 0.56, 3.10],
[-0.62, 0.90, -0.40, 0.35]],
[[-0.22, 0.34, -1.00, 0.96],
[ 0.61, 0.47, -0.27, 2.17],
[ 2.35, -1.06, 0.80, -0.10],
[ 1.92, 0.23, 1.15, -1.35],
[-1.24, -1.06, 1.77, 1.54],
[-0.26, -1.06, 0.20, -0.44]]], grad_fn=<AddBackward0>)本系列的下一篇文章是多头注意力层。
请不要忘记点赞和关注更多!:)
引用
- 辍学层
- 位置编码概述
- PyTorch 的位置编码实现
- 带注释的变压器
- 变压器的位置编码
附录
可视化位置编码的唯一性
在得出结论之前,验证位置编码的唯一性并了解它们如何与更大的序列一起工作将是有益的。
使用 matplotlib,可以轻松地将向量相互比较。
def visualize_pe(max_length, d_model, n):
plt.imshow(gen_pe(max_length, d_model, n), aspect="auto")
plt.title("Positional Encoding")
plt.xlabel("Encoding Dimension")
plt.ylabel("Position Index")
# set the tick marks for the axes
if d_model < 10:
plt.xticks(torch.arange(0, d_model))
if max_length < 20:
plt.yticks(torch.arange(max_length-1, -1, -1))
plt.colorbar()
plt.show()
# plot the encodings
max_length = 10
d_model = 4
n = 100
visualize_pe(max_length, d_model, n)
每行表示一个位置编码向量,每列表示与嵌入组合时将添加到的相应维度。
这也可以在较大的值 n、d_model 和 max_length 中看到:
# plot the encodings
max_length = 1000
d_model = 512
n = 10000
visualize_pe(max_length, d_model, n)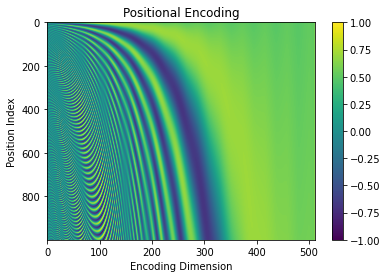
参考资源:Positional Encoding. This article is the second in The… | by Hunter Phillips | Medium