正交表是一种用于多因素实验设计的表格。它可以帮助我们在尽可能少的试验次数下确定各个因素对结果的影响,从而提高实验效率。接下来将从以下几个方面介绍正交表的相关内容。

一、正交表基本概念
正交表是一种特制的表格,用于多因素实验设计研究。根据正交表的正交性,可以从全面试验中挑选尽可能少有代表性的组合进行实验,这些组合具有“均衡分散、整齐可比”的特点。“均衡分散”使得试验点具有代表性;“整齐可比”便于实验数据进行分析。通过正交表进行试验,可以大大节省实验的人力、物力和时间成本,便于确定各个因素对实验结果的影响,从而提高实验效率。
二、正交表的构成
(1)因数与水平
在理解正交表的构成之前,需要先理解进行正交试验因素与水平的概念。
因素:指实验中的变量;例如温度、时间、催化剂种类,共三因素。
水平:指实验因素的不同取值;例如温度分为30℃、50℃、80℃,那么代表温度这个因素是三水平。
通常形容正交试验时,直接说进行几因素几水平正交试验,例如三因素三水平正交试验。
(2)表示形式
正交表通常表现形式为:L_{行数}~(水平数~^{因素数})

L表示正交表,行数表示需要进行的实验次数;因素数代表实验中变量的个数,即正交表中列的个数;水平数代表每个因素的水平数。其中行数=因素数*(水平数-1)+1
举例说明:例如正交表L_{9}~(3~^{4}),L右下角数字“9”表示有9行,即需要做9次实验。括号内指数“4”代表有4列,即最多可观察4个因素。括号内数“3”表示每个因素均为3水平,即表的主体部分只有数字1,2,3,分别代表水平1,2,3。四因素三水平试验如果进行全面试验需要进行3~^{4}=81次实验,而进行正交试验只需要进行9次即可,大大增加了实验效率。四因素三水平正交设计表如下图所示:
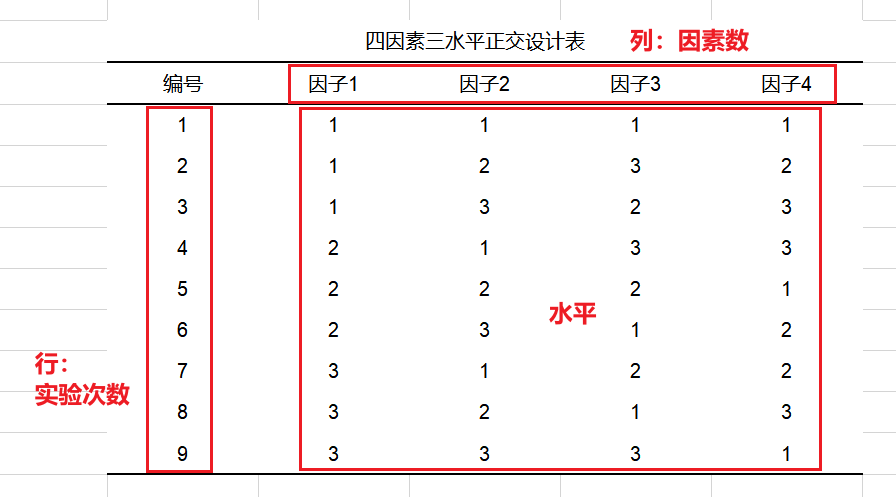
图1
当正交表中各个因素的水平数不同时,此时称它为混合型正交表,例如正交表L_{8}~(4~^{1}2~^{4}),表示在此表的5列中,有1列为4水平,4列为2水平。
三、正交表的性质
正交表必须同时满足以下两个性质:
①整齐可比性——每一列中不同数字出现的次数相等
即每个因素的每个水平出现的次数是完全相同的。由于在试验中每个因素的每个水平与其他因素的每个水平参与试验的机率是相同的,这就保证了再各个水平中最大程度的排除了其他因素水平的干扰,能最有效的进行比较,进而容易找到最优的实验条件。
例如在图1四因素三水平正交试验表中,每一列中数字1,2,3出现的次数都是3次,满足整齐可比性。
②均衡分散性——任意两列的数字排列方式齐全且均衡
即任意两个因素的水平搭配是完全相同的(任意两列横向组成的数字对中,每对数字出现的次数相等)。这样就保证了实验条件均衡地分散在因素水平的完全组合中,具有很强的代表性。
例如在图1的三水平试验中,任意两列数字对共有9种,(1,1)(1,2)(1,3)(2,1)(2,2)(2,3)(3,1)(3,2)(3,3),且每对出现均数相等。
四、正交表的生成
正交表的设计需要用到组合数学和概率学知识,手动设计正交表耗时费力,目前很多软件都能在线生成正交表,接下来介绍如何使用在线数据分析软件SPSSAU快速生成正交表。
SPSSAU提供两种方式生成正交表,说明如下:
(1)自动生成正交表
在【试验/医学研究】模块,选择分析方法【正交试验】,依次选择因子(因素)个数和水平数,点击开始分析即可得到最接近的正交表。以三因素三水平为例,操作如下图:
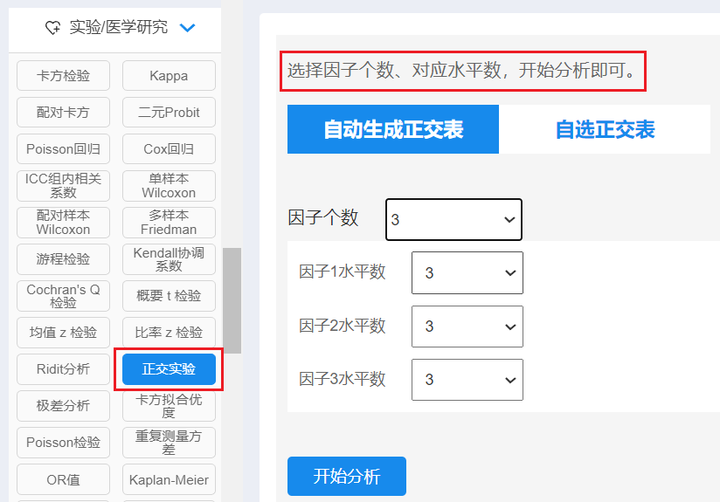
图2
此时SPSSAU输出三因素三水平正交设计表如下图:
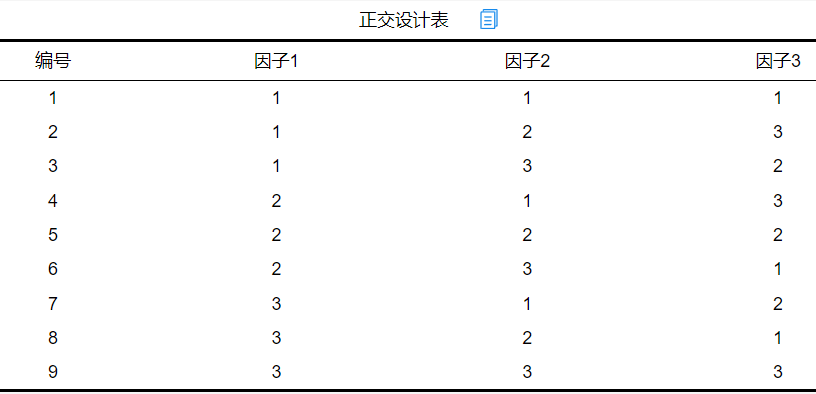
(2)自选正交表
如果知道自己需要什么样的正交表,可通过自选正交表生成。可以下拉选择常用正交表:

图3
或者输入正交表ID,当前SPSSAU共提供183种正交表,可点击“下载按钮”查看SPSSAU正交表手册,展示部分如下图:

图4
(3)正交表修改
由软件自动提供正交表后,很可能并不满足完全满足预期,因此需要进行以下处理。
①如果有超出的多余因子,直接删除即可;由于正交表任意两列之间均满足正交性,所以删除某列后并不影响。
②‘拟水平法’:如果某因子的水平数比预期多,比如生成正交表的因子1有5个水平,但只需要4个水平;那么此时把多出的数字5(第5个水平),直接用其它4个水平中任意一个或多个替换填补即可。此种处理叫‘拟水平法’。‘拟水平法’在正交表改造处理中非常常见,但‘拟水平法’后,可能就不再具有正交表特性,这是非常正常的;
③‘组合法’:比如考虑2水平,4水平,8水平;并不需要一定使用2.1.4.1.8.1;而是使用比如L12.2.11(因为2水平有16个,可拆分成:2,2*2,2*2*2,共用掉6个因子,都还余5个因子没有使用直接删除即可),组合法是一种正交表获取的技巧操作法,该操作法是在正交表生成前自行处理和选择,以及‘组合法’对于正交性没有任何影响,只是一种手工选择正交表的技巧做法;
④‘并列法’: 指把两列或多列,合并成1列,比如有两个因子其中1个为2水平另1个为3水平;把两个因子合并变成2*3=6水平;‘并列法’是自主手工选择正交表的一种技巧式做法,‘并列法’后正交性还在。
五、正交实验设计与分析步骤
进行多因素正交试验设计与分析的通常步骤如下:
①确定因素与水平(与实验设计相关);
②使用软件生成相应正交表(SPSSAU可快速生成正交表);
③根据正交表进行正交试验,得到试验结果;
④使用极差分析或方差分析对试验进行分析,得到最优试验条件。