一种递归式的非零自然数全分解方法_Weiming Chen的博客-CSDN博客

简单来说，就是单调不减，后一个数大于等于前一个数

像这样，那么我们只需给定前一个数和后一个数就可以进行递归操作

#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;

int func(int pre ,int now){
    if (now==0 )return 1;
    // 1 2 7 ==> 1 2 2 5 /1 2 3 4
    // 接下来分解出来所有的数都应该 >=pre
    int temp=0;
    for (int i=1;2*i<=now;i++){
        if (i>=pre){
            temp+=func(i,now-i);
            temp++;
        }
    }
    return temp;
}
int main(){
    int n;
    scanf("%d",&n);


    printf("%d",func(0,n));
    return 0;
}

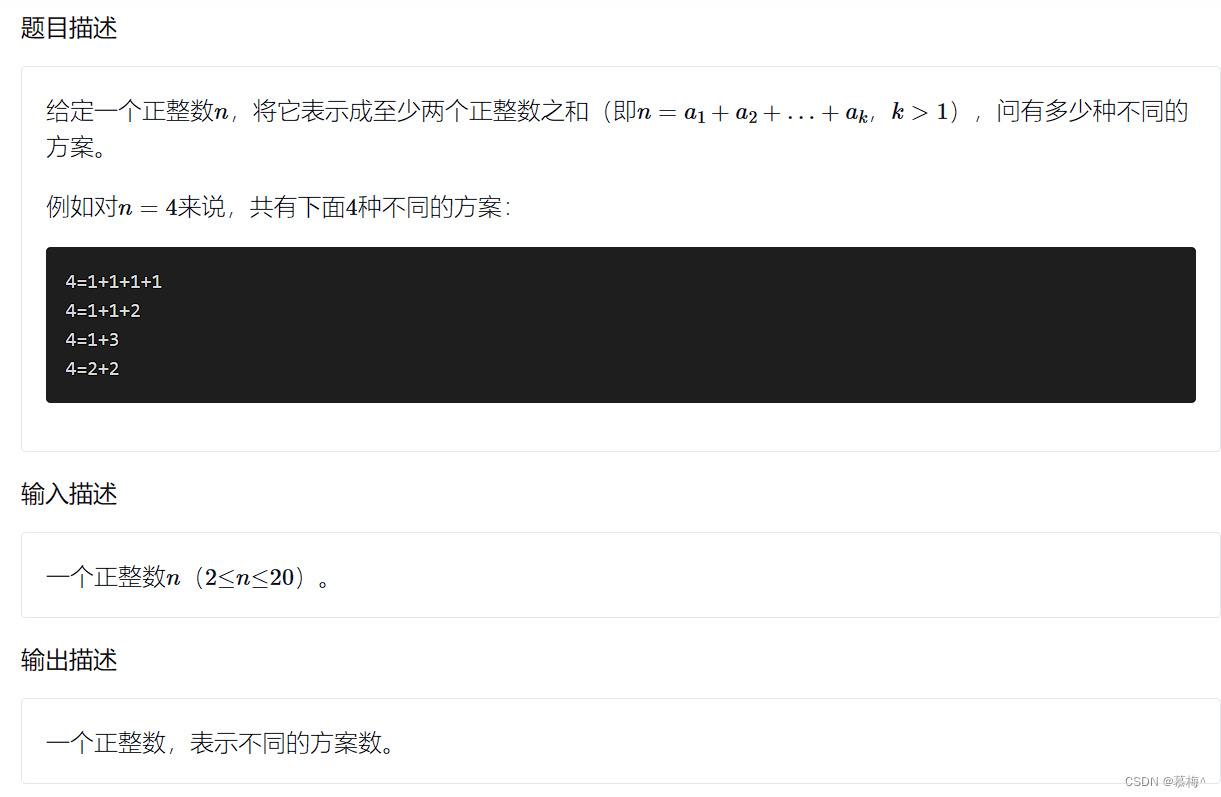
例如7，我们假设其前一个数为0，带入递归函数func(0,7) pre = 0,now =7 表示现在要拆分的数为7

首先获得所有的可能的分解组合例如1-6  2-5  3-4

当然这里直接使用

for (int i=1;2*i<=now;i++)

就可以获得递增的全部组合。

因为我们 拆分的是now = 7，那么拆分出来的第一个数要大于等于pre = 0

如果符合那么我们就可以累加，值得注意的是，我们1-6本身也是一个拆分的组合，因此temp++

递归的边界就是，当我们需要拆分的数为1时，表示无法拆分，而由于其本身已经在上一次的temp++加过了，因此返回0。

总的来说func(pre,now)表示拆分的个数，本身这个组合通过temp++进行计算。