不同路径（medium）

题目链接:

62. 不同路径

题目描述:

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。问总共有多少条不同的路径？

示例 1：

输入：m = 3, n = 7
输出：28

题目解析

机器人在左上角,我们可以向下走一格或者向右走一格,问一问我们有多少路径可以走到右下角.

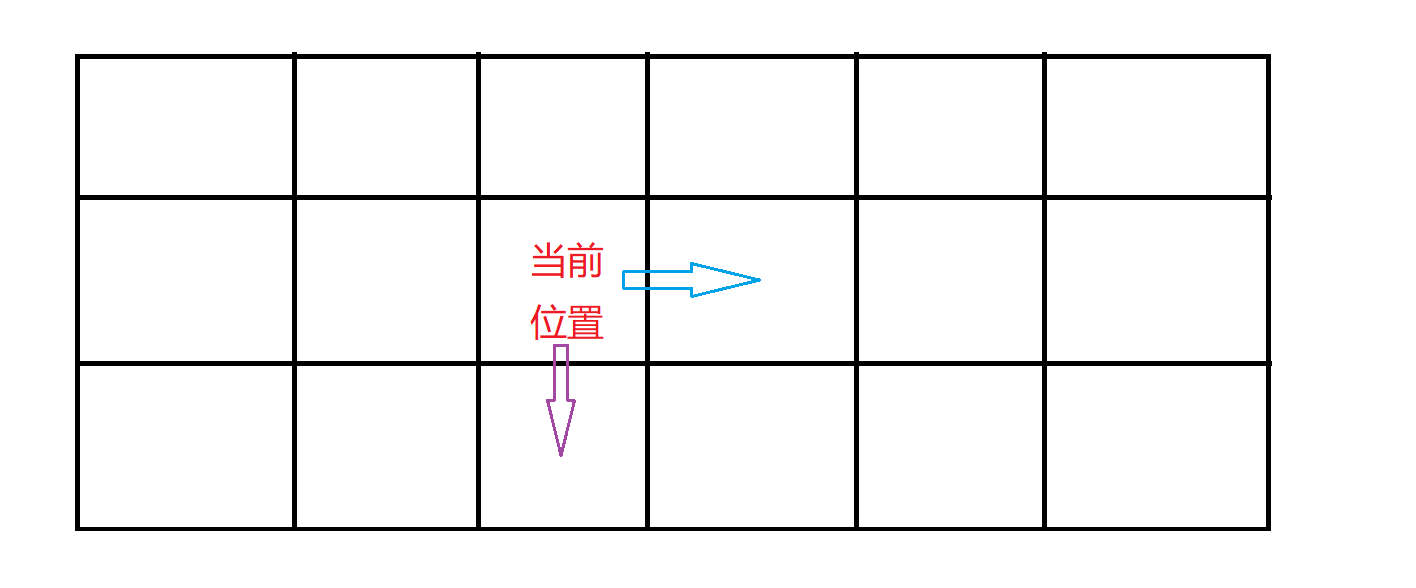
这里要注意的是,我们求得是路径数.

算法原理

状态表示

按照经验,我们以…为结尾表示状态.

dp[i][j]: 表示我们到达下标为[i,j]位置的总共的路径数.

状态转移方程

我们向一下,怎么可以到达[i,j]位置,可以很容易的想到,我们[i-1,j]向下走一格,或者是[i,j-1]向右走一格.由于我们求得是路径数,那么此时状态方程为dp[i][j] = dp[i-1][j] + dp[i][j-1].

初始化

这里用的i-1和j-1,所以我们这里加上辅助接点.加上辅助接点需要注意是我们下标对真实数组下标的映射.

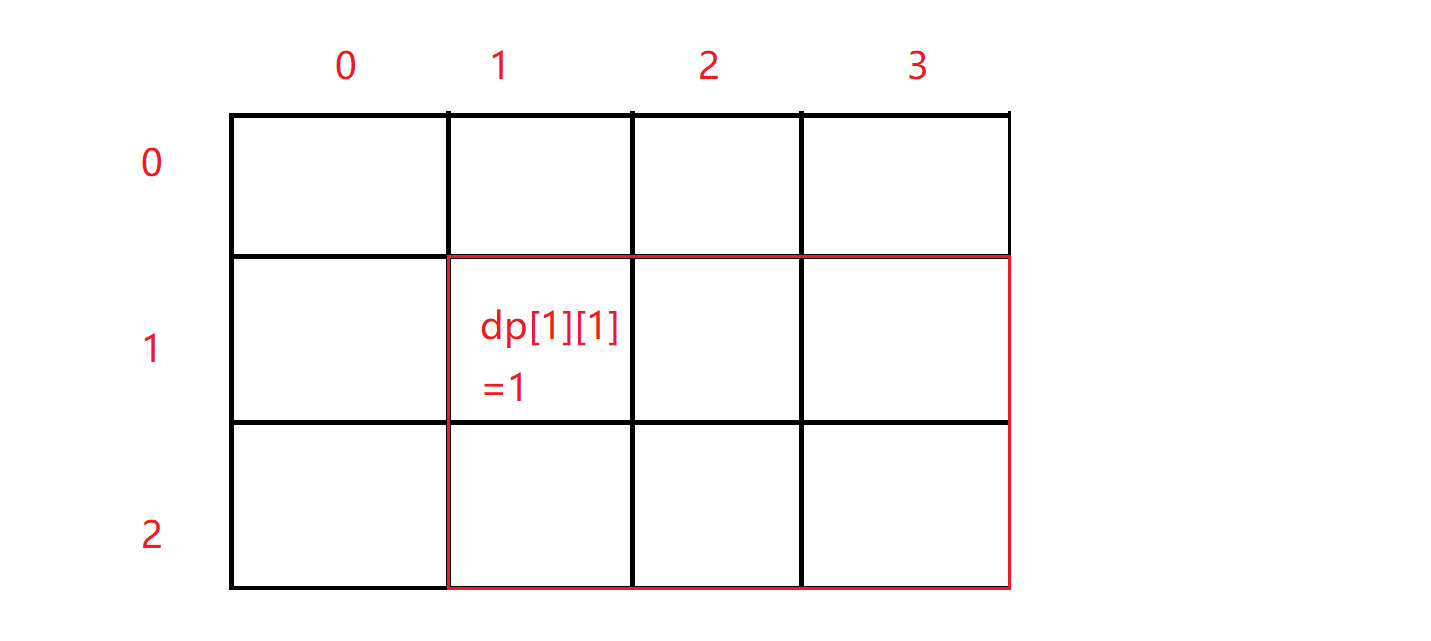
为了使dp[1][1]数据有效,我们这里让dp[0][1] = 1 && dp[1][0] = 0或者dp[0][1] = 0 && dp[1][0] = 1就可以了.

填表顺序

和前面一样从左先右,大方向从上向下.

返回值

返回dp[n][m]

编写代码

class Solution
{
public:
  int uniquePaths(int m, int n)
  {
    // 参数检测
    std::vector<std::vector<int>> dp(m + 1, std::vector<int>(n + 1, 0));
    // dp[0][1] = 1;
    dp[1][0] = 1;
    for (size_t i = 1; i <= m; i++)
    {
      for (size_t j = 1; j <= n; j++)
      {
        dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
      }
    }

    return dp[m][n];
  }
};

不同路径II（medium）

题目链接:

63. 不同路径 II

题目描述:

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？网格中的障碍物和空位置分别用 1 和 0 来表示。

示例1:

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

题目解析

和上面一样,只不过我们这里有障碍物,存在障碍物的路径是不作数的.

算法原理

状态表示

经验,dp[i][j]表示到达[i,j]位置的总路径数.

状态转移方程

这里有障碍物,首先我们要判断[i,j]是不是障碍物.

初始化

和上面一样.

填表顺序

从左先右.

返回值

返回dp[n][m]

编写代码

class Solution
{
public:
  int uniquePathsWithObstacles(vector<vector<int>> &obstacleGrid)
  {
    // 参数判断
    int n = obstacleGrid.size();
    int m = obstacleGrid.back().size();
    std::vector<std::vector<int>> dp(n + 1, std::vector<int>(m + 1, 0));
    dp[0][1] = 1;

    for (size_t i = 1; i <= n; i++)
    {
      for (size_t j = 1; j <= m; j++)
      {
        if (obstacleGrid[i - 1][j - 1] == 0)
          dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
      }
    }
    return dp[n][m];
  }
};

礼物的最大价值（medium）

题目链接:

剑指 Offer 47. 礼物的最大价值

题目描述:

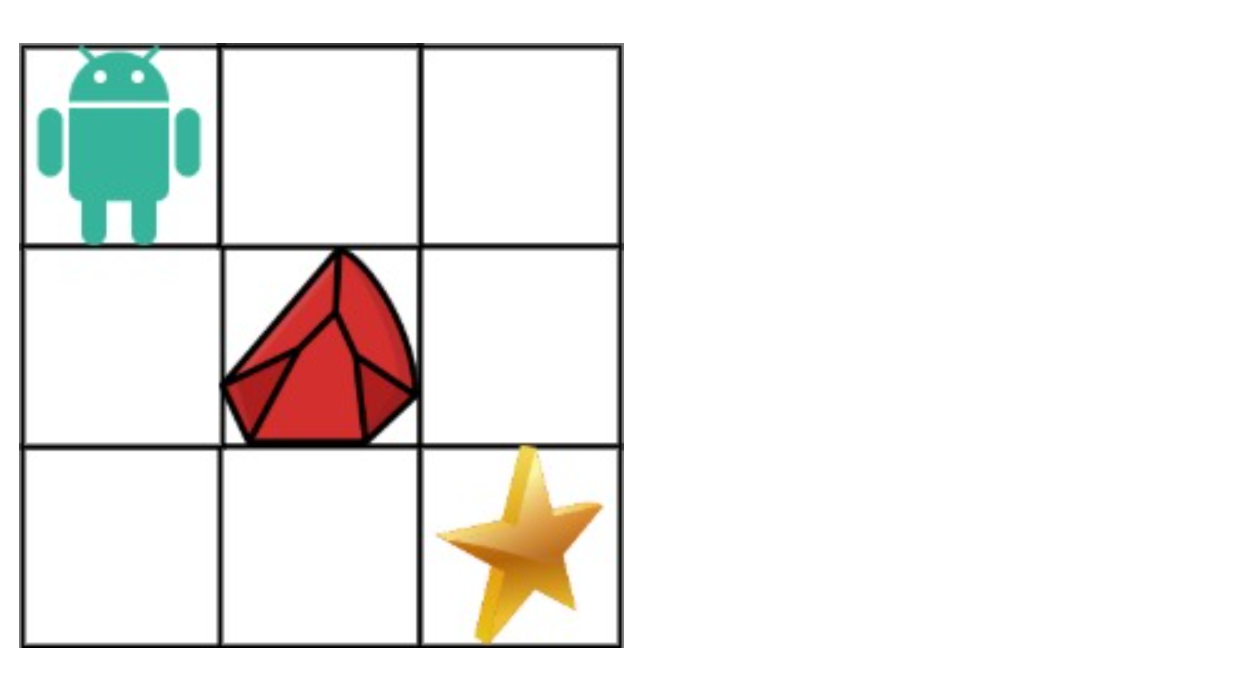
在一个 m*n 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值，请计算你最多能拿到多少价值的礼物？

示例 1:

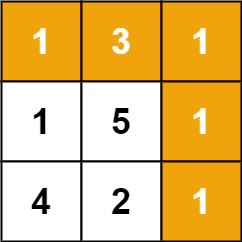
输入: 
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物

题目解析

我们从左上角跳到右下角的过程中,每个格子都有礼物,到达一个格子就可以得到这个礼物.求我们这个过程中我们可以得到礼物的最大价值.

算法原理

状态表示

题目+经验.dp[i][j]:表示到达[i,j]位置我们得到最大价值的价值数.

状态转移方程

可以先上面和左面到达[i,j]位置,但是这两个情况我们只能选择一种,那么此时选择最大价值的一种dp[i][j] = max(dp[i-1][j], dp[i][j-1])+value[i][j]

初始化

这里也加上一个辅助行和列.

填表顺序

从左先右.

返回值

返回dp[n][m]

编写代码

class Solution
{
public:
  int maxValue(vector<vector<int>> &grid)
  {
    int n = grid.size();
    int m = grid.back().size();
    std::vector<std::vector<int>> dp(n + 1, std::vector<int>(m + 1, 0));
    for (size_t i = 1; i <= n; i++)
    {
      for (size_t j = 1; j <= m; j++)
      {

        dp[i][j] = std::max(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];
      }
    }
    return dp[n][m];
  }
};

下降路径最小和（medium）

题目链接:

[931. 下降路径最小和](https://leetcode.cn/problems/three-steps-problem-lcci/)

题目描述:

给你一个 n x n 的 方形 整数数组 matrix ，请你找出并返回通过 matrix 的下降路径 的 最小和 。下降路径 可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。

示例 1：

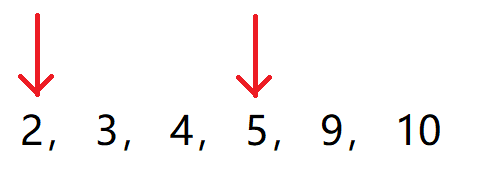
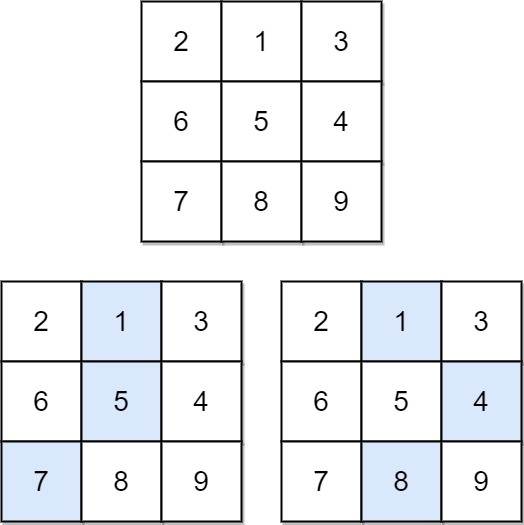
输入：matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出：13
解释：如图所示，为和最小的两条下降路径

题目解析

很简单,我们可以通过三种方式到达x位置处.

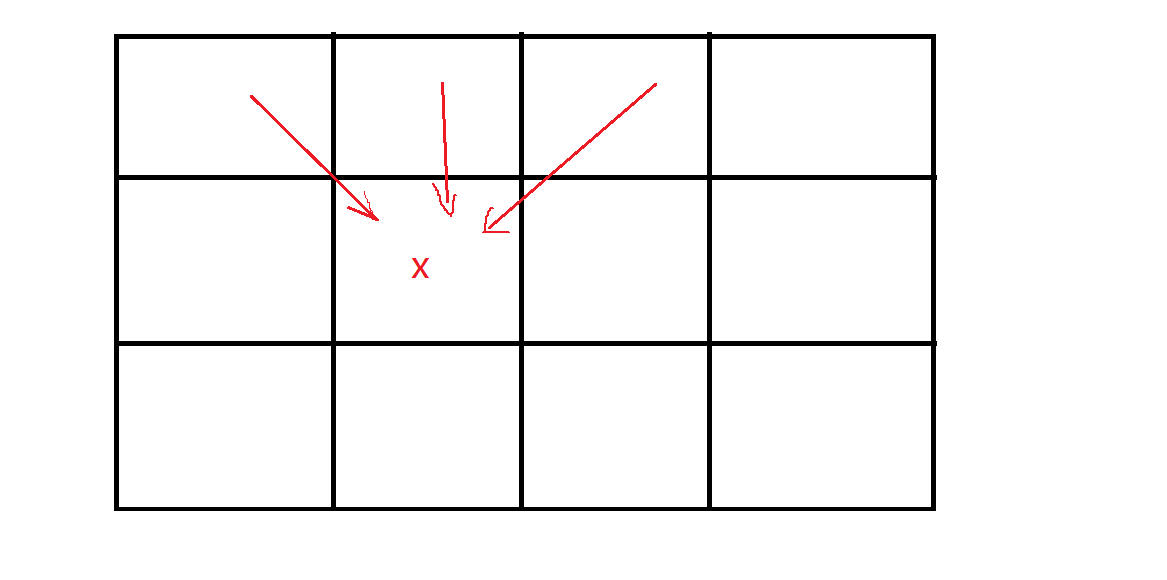
题目上求从第一行的任意位置通过规则走到最后一行,求我们的和最小.

算法原理

状态表示

dp[i][j]: 以[i,j]位置为结尾,我们的最小的路径和

状态转移方程

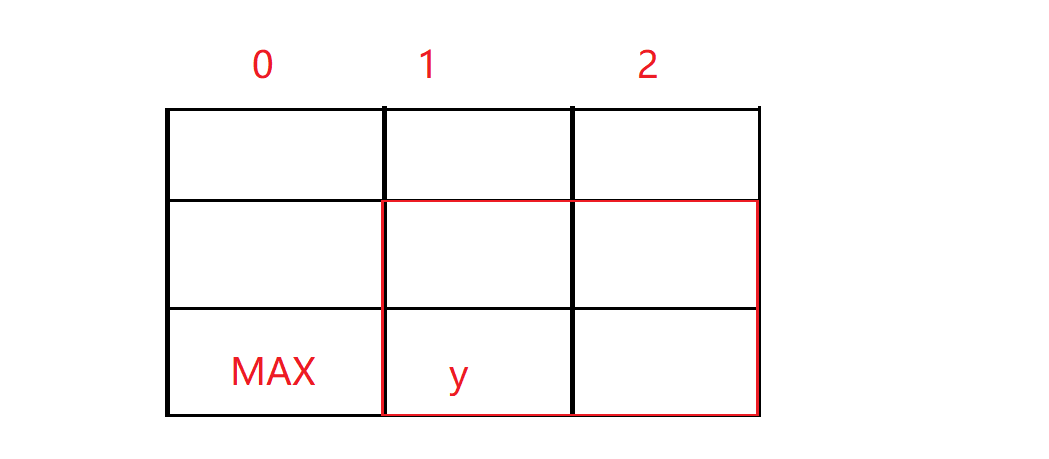
dp[i][j] = min(dp[i-1][j], dp[i-1][j+1], dp[i-1][j-1])

初始化

我们这里要求了i-1和j-1已经j+1,此时我们这么添加辅助的.

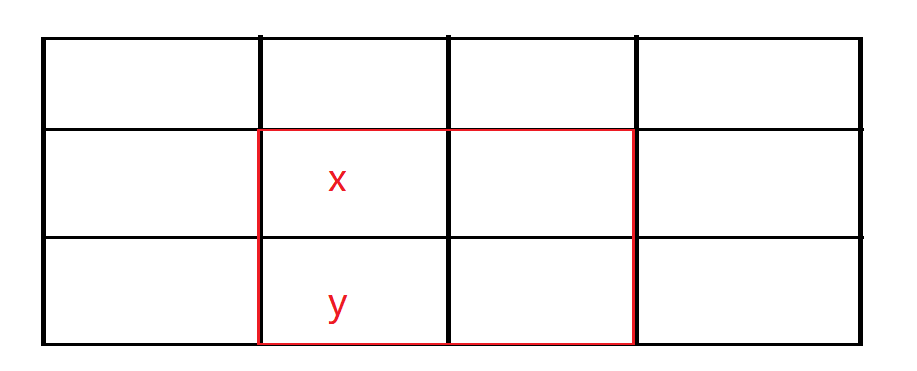
对于x这一行,他依赖上面的三个,所以第一行必须是0.对于y这一列,以y来举例子.我们发现y这一个,我们发现它依赖x这个数,所以x左侧的数据一定要被抛弃,那么我们初始化值大点.

填表顺序

上->下,左->右

返回值

我们求到达最后一行的最小路径和,所以要遍历一遍.

编写代码

class Solution
{
public:
  int minFallingPathSum(vector<vector<int>> &matrix)
  {
    int n = matrix.size();
    int m = matrix.back().size();
    std::vector<std::vector<long long>> dp(n + 1, std::vector<long long>(m + 2,INT_MAX));
    for (size_t i = 0; i <= m; i++)
    {
      dp[0][i] = 0;
    }
    for (size_t i = 1; i <= n; i++)
    {
      for (size_t j = 1; j <= m; j++)
      {
        dp[i][j] = (long long)(std::min(dp[i - 1][j], std::min(dp[i - 1][j + 1], dp[i - 1][j - 1])) + (long long)matrix[i - 1][j - 1]);
      }
    }
    long long minVal = dp[n][0];
    for (size_t i = 1; i <= m; i++)
    {
      minVal = std::min(minVal, dp[n][i]);
    }
    return minVal;
  }
};

最小路径和（medium）

题目链接:

64. 最小路径和

题目描述:

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

**说明：**每次只能向下或者向右移动一步。

示例 1：

输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

题目解析

这个比上面那个简单.

算法原理

状态表示

dp[i][j]: 表示到达[i,j]位置我们路径和最小

状态转移方程

dp[i][j] = min(dp[i-1][j], dp[i][j-1])+ v[i][j]

初始化

只需要保证dp[0][1] = 0

填表顺序

从左先右.

返回值

return dp[n][m];

编写代码

class Solution
{
public:
  int minPathSum(vector<vector<int>> &grid)
  {
    int n = grid.size();
    int m = grid.back().size();
    std::vector<std::vector<int>> dp(n + 1, std::vector<int>(m + 1, INT_MAX));
    dp[0][1] = 0;
    for (size_t i = 1; i <= n; i++)
    {
      for (size_t j = 1; j <= m; j++)
      {
        dp[i][j] = std::min(dp[i][j - 1], dp[i - 1][j]) + grid[i - 1][j - 1];
      }
    }
    return dp[n][m];
  }
};

地下城游戏（hard）

题目链接:

174. 地下城游戏

题目描述:

恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里，他必须穿过地下城并通过对抗恶魔来拯救公主。

骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下，他会立即死亡。

有些房间由恶魔守卫，因此骑士在进入这些房间时会失去健康点数（若房间里的值为负整数，则表示骑士将损失健康点数）；其他房间要么是空的（房间里的值为 0），要么包含增加骑士健康点数的魔法球（若房间里的值为正整数，则表示骑士将增加健康点数）。

为了尽快解救公主，骑士决定每次只 向右 或 向下 移动一步。

返回确保骑士能够拯救到公主所需的最低初始健康点数。

**注意：**任何房间都可能对骑士的健康点数造成威胁，也可能增加骑士的健康点数，包括骑士进入的左上角房间以及公主被监禁的右下角房间。

示例 1：

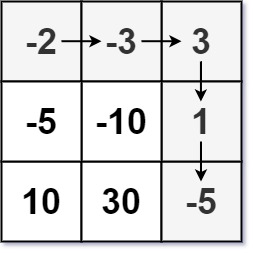
输入：dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]]
输出：7
解释：如果骑士遵循最佳路径：右 -> 右 -> 下 -> 下 ，则骑士的初始健康点数至少为 7 。

题目解析

勇士通过走路的规则,我们有最少多少血可以走到右下角.

算法原理

状态表示

继续按照上面的思想来.

以 … 为结尾.dp[i][j]: 以[i,j]位置为结尾,我们需要最少的点数.这里有一个问题,我们的状态只能保证可以到达[i,j]位置,但是不能保证一定会到达右下角.

以 … 为开始.dp[i][j]: 以[i,j]位置为开始到达右小角需要最少的点数,这个是可以的.

状态转移方程

对于 dp[i][j] ，从 [i, j] 位置出发，下一步会有两种选择（为了方便理解，设 dp[i][j] 的最终答案是 x ）：

1. 走到右边，然后走向终点
   那么我们在 [i, j] 位置的最低健康点数加上这一个位置的消耗，应该要大于等于右边位置的最低健康点数，也就是： x + dungeon[i][j] >= dp[i][j + 1] 。通过移项可得： x >= dp[i][j + 1] - .dungeon[i][j] 。因为我们要的是最小
   值，因此这种情况下的x = dp[i][j + 1] - dungeon[i][j]
2. 走到下边，然后走向终点
   那么我们在 [i, j] 位置的最低健康点数加上这一个位置的消耗，应该要大于等于下边位置的最低健康点数，也就是： x + dungeon[i][j] >= dp[i + 1][j] 。通过移项可得：x >= dp[i + 1][j] - dungeon[i][j]。因为我们要的是最小
   值，因此这种情况下的x = dp[i + 1][j] - dungeon[i][j]

综上所述，我们需要的是两种情况下的最小值，因此可得状态转移方程为：
dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j]
但是，如果当前位置的 dungeon[i][j] 是一个比较大的正数的话，dp[i][j]的值可能变成 0 或者负数。也就是最低点数会小于 1 ，那么骑士就会死亡。因此我们求出来的 dp[i][j] 如果小于等于 0 的话，说明此时的最低初始值应该为 1 。处理这种情况仅需让 dp[i][j] 与 1 取一个最大值即可：dp[i][j] = max(1, dp[i][j])

初始化

这里留给大家.

填表顺序

右->左,下->上

返回值

题目要求给定一个n,求到达第n个台阶的方法数,这里就是dp[n]

编写代码

class Solution
{
public:
  int calculateMinimumHP(vector<vector<int>> &dungeon)
  {
    int m = dungeon.size(), n = dungeon[0].size();
    // 建表 + 初始化
    vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));
    dp[m][n - 1] = dp[m - 1][n] = 1;
    // 填表
    for (int i = m - 1; i >= 0; i--)
      for (int j = n - 1; j >= 0; j--)
      {
        dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j];
        dp[i][j] = max(1, dp[i][j]);
      }
    // 返回结果
    return dp[0][0];
  }
};