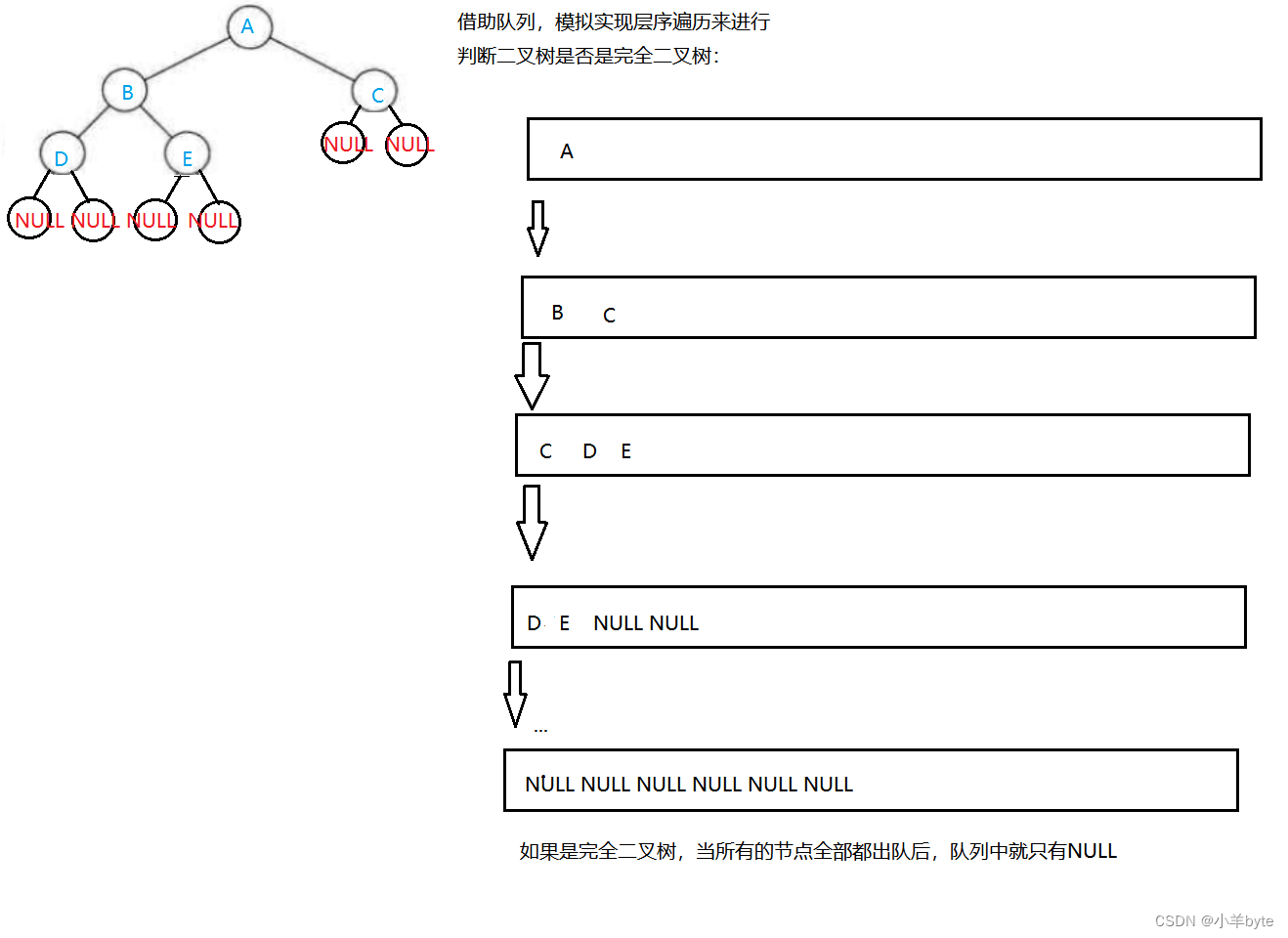
今天我们看一道 leetcode hard 难度题目:地下城游戏。
恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快解救公主,骑士决定每次只 向右 或 向下 移动一步。
返回确保骑士能够拯救到公主所需的最低初始健康点数。
注意:任何房间都可能对骑士的健康点数造成威胁,也可能增加骑士的健康点数,包括骑士进入的左上角房间以及公主被监禁的右下角房间。
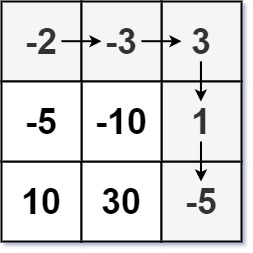
输入:
dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]]输出:
7解释:如果骑士遵循最佳路径:右 -> 右 -> 下 -> 下 ,则骑士的初始健康点数至少为 7 。
思考
挺像游戏的一道题,首先只能向下或向右移动,所以每个格子可以由上面或左边的格子移动而来,很自然想到可以用动态规划解决。
再想一想,该题必须遍历整个地下城而无法取巧,因为最低健康点数无法由局部数据算出,这是因为如果不把整个地下城走完,肯定不知道是否有更优路线。
动态规划
二维迷宫用两个变量 i j 定位,其中 dp[i][j] 描述第 i 行 j 列所需的最低 HP。
但最低所需 HP 无法推断出是否能继续前进,我们还得知道当前 HP 才行,比如:
// 从左到右走
3 -> -5 -> 6 -> -9在数字 6 的位置所需最低 HP 是 3,但我们必须知道在 6 时勇者剩余 HP 才能判断 -9 会不会直接导致勇者挂了,因此我们将 dp[i][j] 结果定义为一个数组,第一项表示当前 HP,第二项表示初始所需最低 HP。
代码实现如下:
function calculateMinimumHP(dungeon: number[][]): number {
// dp[i][j] 表示 i,j 位置 [当前HP, 所需最低HP]
const dp = Array.from(dungeon.map(item => () => [0, 0]))
// dp[i][j] = 所需最低HP最低(dp[i-1][j], dp[i][j-1])
dp[0][0] = [
dungeon[0][0] > 0 ? 1 + dungeon[0][0] : 1,
dungeon[0][0] > 0 ? 1 : 1 - dungeon[0][0]
]
for (let i = 0; i < dungeon.length; i++) {
for (let j = 0; j < dungeon[0].length; j++) {
if (i === 0 && j === 0) {
continue
}
const paths = []
if (i > 0) {
paths.push([i - 1, j])
}
if (j > 0) {
paths.push([i, j - 1])
}
const pathResults = paths.map(path => {
let leftMaxHealth = dp[path[0]][path[1]][0] + dungeon[i][j]
// 剩余HP大于 0 则无需刷新最低HP,否则尝试刷新取最大值
let lowestNeedHealth = dp[path[0]][path[1]][1]
if (leftMaxHealth <= 0) {
// 最低要求HP补上差价
lowestNeedHealth += 1 - leftMaxHealth
// 最低需要HP已补上,所以剩余HP也变成了 1
leftMaxHealth = 1
}
return [leftMaxHealth, lowestNeedHealth]
})
// 找到 pathResults 中 lowestNeedHealth 最小项
let minLowestNeedHealth = Infinity
let minIndex = 0
pathResults.forEach((pathResult, index) => {
if (pathResult[1] < minLowestNeedHealth) {
minLowestNeedHealth = pathResult[1]
minIndex = index
}
})
dp[i][j] = [pathResults[minIndex][0], pathResults[minIndex][1]]
}
}
return dp[dungeon.length - 1][dungeon[0].length - 1][1]
};首先计算初始位置 dp[0][0],因为只看这一个点,因此如果有恶魔,最少初始 HP 为能击败恶魔后自己剩 1 HP 就行了,如果房间是空的,至少自己 HP 得是 1(否则勇者进迷宫之前就挂了),如果有魔法球,那么初始 HP 为 1(一样防止进迷宫前挂了)。
初始 HP 稍有不同,如果房间是空的或者有恶魔,那打完恶魔之后最多剩 1 HP 最经济,所以此时 HP 初始值就是 1,如果有魔法球,那么一方面为了防止进入迷宫前自己就挂了,得有个初始 1 的 HP,魔法球又必须得吃,所以 HP 是 1 + 魔法球。
接着就是状态转移方程了,由于 dp[i][j] 可以由 dp[i-1][j] 或 dp[i][j-1] 移动得到(注意 i 或 j 为 0 时的场景),因此我们判断一下从哪条路过来的最低初始 HP 最低就行了。
如果进入当前房间后,房间是空的,有魔法球,或者当前 HP 可以打败恶魔,则不影响最低初始 HP,如果当前 HP 不足以击败恶魔,则我们把缺的 HP 给勇者在初始时补上,此时极限一些还剩 1 HP,得到一个最经济的结果。
然后我们提交代码发现,无法 AC!下面是一个典型挂掉的例子:
1 -3 3
0 -2 0
-3 -3 -3我们把 DP 中间过程输出,发现右下角的 5 大于最优答案 3.
[
[ 2, 1 ], [ 1, 3 ], [ 4, 3 ]
[ 2, 1 ], [ 1, 2 ], [ 1, 2 ]
[ 1, 3 ], [ 1, 5 ], [ 1, 5 ]
]观察发现,勇者先往右走到头,再往下走到头答案就是 3,问题出在 i=1,j=2 处,也就是中间行最右列的 [1, 2]。但从这一点来看,勇者从左边过来比从上面过来需要的初始 HP 少,因为左边是 [1, 2] 上面是 [4, 3],但这导致了答案不是最优解,因为此时剩余 HP 不够,右下角是一个攻击为 3 的恶魔,而如果此时我们选择了初始 HP 高一些的 [4, 3],换来了更高的当前 HP,在不用补初始 HP 的情况就能把右下角恶魔干掉,整体是更划算的。
如果此时我们在玩游戏,读读档也就能找到最优解了,但悲剧的是我们在写一套算法,我们发现当前 DP 项居然还可能由后面的值(攻击力为 3 的恶魔)决定! 用专业的话来说就是有后效性导致无法使用 DP。
我们在判断每一步最优解时,其实有两个同等重要的因素影响判断,一个是初始最少所需 HP,它的重要度不言而喻,我们最终就希望这个答案尽可能小;但还有当前 HP 呢,当前 HP 高意味着后面的路会更好走,但我们如果不往后看,就不知道后面是否有恶魔,自然也不知道要不要留着高当前 HP 的路线,所以根本就无法根据前一项下结论。
因为考虑的因素太多了,我们得换成游戏制作者的视角,假设作为游戏设计者,而不是玩家,你会真的从头玩一遍吗?如果真的要设计这种条件很极限的地下城,设计者肯定从结果倒推啊,结果我们勇者就只剩 1 HP 了,至于路上会遇到什么恶魔或者魔法球,反过来倒推就一切尽在掌握了。所以我们得采用从右下角开始走的逆向思维。
逆向思维
为什么从结果倒推,DP 判断条件就没有后效性了呢?
先回忆一下从左上角出发的情况,为什么除了最低初始 HP 外还要记录当前 HP?原因是当前 HP 决定了当前房间的怪物勇者能否打得过,如果打不过,我们得扩大最低初始 HP 让勇者能在仅剩 1 HP 的情况险胜当前房间的恶魔。但这个当前 HP 值不仅要用来辅助计算最低初始 HP,它还有一个越大越好的性质,因为后面房间可能还有恶魔,得留一些 HP 预防风险,而 "最低初始 HP" 尽可能低与 "当前 HP" 尽可能高,这两个因素无法同时考虑。
那为什么从右下角,以终为始的考虑就可以少判断一个条件了呢?首先最低初始 HP 我们肯定要判断的,因为答案要的就是这个,那当前 HP 呢?当前 HP 重要吗?不重要,因为你已经拯救到公主了,而且是以最低 HP 1 点的状态救到了公主,按故事路线逆着走,遇到恶魔房间,恶魔攻击是多少我就给你加多少初始 HP,遇到魔法球恢复了我就给你扣对应初始 HP,总之能让你正好战胜恶魔,魔法球补给你的 HP 我也扣掉,就可以了。核心区别是,此时当前 HP 已经不会影响最低初始 HP 了,因为初始 HP 就是从头推的,我们反着走地下城,每次实际上都是在判断这个点作为起点时的状态,所以与之前的路径无关。
代码很简单,如下:
function calculateMinimumHP(dungeon: number[][]): number {
// dp[i][j] 表示 i,j 位置最少HP
const dp = Array.from(dungeon.map(item => () => [0, 0]))
// 右下角起始 HP 1,遇到怪物加血,遇到魔法球扣血,实际上就是 -dungeon 计算
const si = dungeon.length - 1
const sj = dungeon[0].length - 1
dp[si][sj] = dungeon[si][sj] > 0 ? 1 : 1 - dungeon[si][sj]
for (let i = si; i >= 0; i--) {
for (let j = sj; j >= 0; j--) {
if (i === si && j === sj) {
continue
}
const paths = []
if (i < si) {
paths.push([i + 1, j])
}
if (j < sj) {
paths.push([i, j + 1])
}
const pathResults = paths.map(path => dp[path[0]][path[1]] - dungeon[i][j])
// 选出最小 HP 作为 dp[i][j],但不能小于 1
dp[i][j] = Math.max(Math.min(...pathResults), 1)
}
}
return dp[0][0]
};逆向思维为什么就能减少当前 HP(或者说路径和,或者说所有之前节点的影响)判断呢?我猜你大概率还是没彻底明白。因为这个思考非常关键,可以说是这道题 99% 的困难所在,还是画个图解释一下:
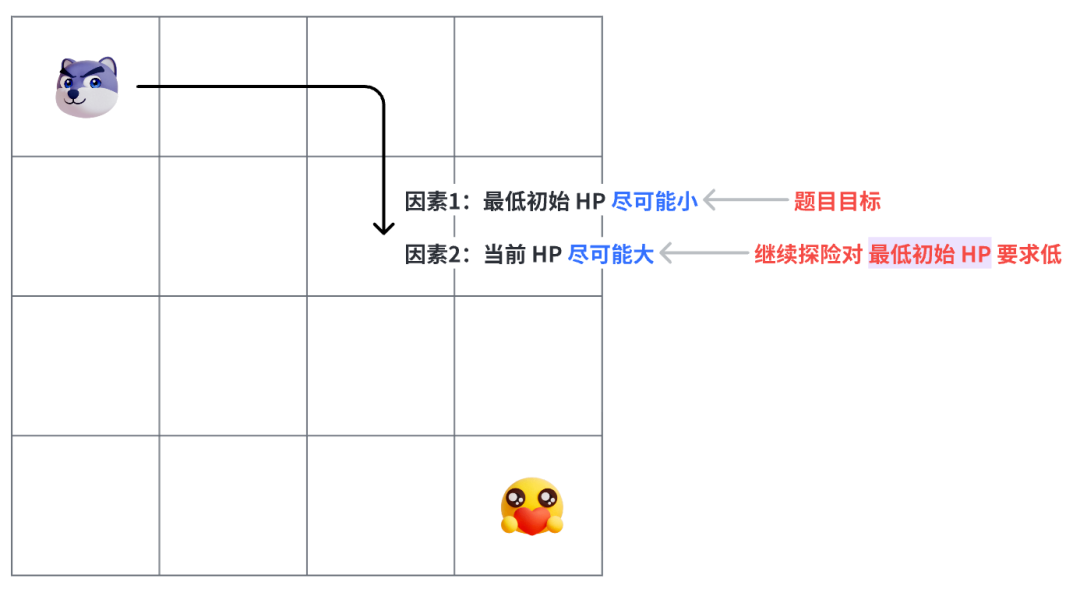
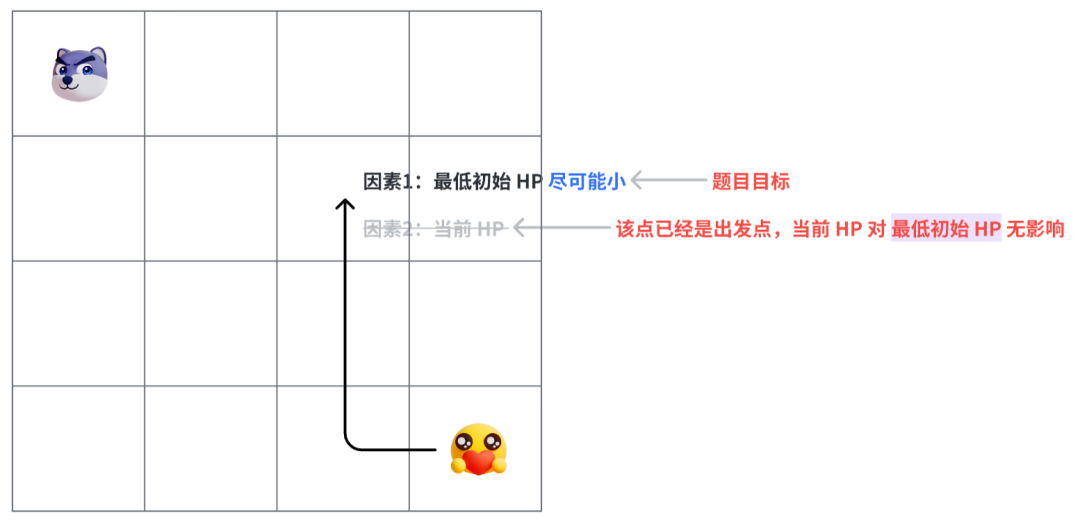
上图是勇者正常探险的思路,下面是逆向(或公主救勇者)的思路。
总结
该题很容易想到使用动态规划解决,但因为目标是求最低的初始健康点需求,所以按照勇者路径走的话,后续未探索的路径会影响到目标,所以我们需要从公主角度反向寻找勇者,才可以保证动态规划的每个判断点都只考虑一个影响因素。
讨论地址是:精读《算法 - 地下城游戏》· Issue #498 · dt-fe/weekly
如果你想参与讨论,请 点击这里,每周都有新的主题,周末或周一发布。前端精读 - 帮你筛选靠谱的内容。
版权声明:自由转载-非商用-非衍生-保持署名(创意共享 3.0 许可证)