保形三次hermit插值
一、算法实现
一、插值函数建立
设函数
y
=
F
(
x
)
y=F(x)
y=F(x)在区间
[
a
,
b
]
[a,b]
[a,b]上有定义,且已知在离散点
a
=
x
0
<
x
1
<
.
.
.
<
x
n
=
b
a=x_0<x_1<...<x_n = b
a=x0<x1<...<xn=b上的值
y
0
,
y
1
,
.
.
.
y
n
,
y_0,y_1,...y_n,
y0,y1,...yn,
f
(
x
)
f(x)
f(x)在
[
x
j
,
x
j
+
1
]
[x_j,x_{j+1}]
[xj,xj+1]分段区间内可表示为
f
(
x
)
=
a
(
x
−
x
j
)
3
+
b
(
x
−
x
j
)
2
+
c
(
x
−
x
j
)
+
d
f(x) = a(x-x_j)^3 +b(x-x_j)^2 + c(x-x_j) + d
f(x)=a(x−xj)3+b(x−xj)2+c(x−xj)+d
设
f
′
(
x
)
f'(x)
f′(x)是一阶导数,则
f
′
(
x
)
=
3
a
(
x
−
x
j
)
2
+
2
b
(
x
−
x
j
)
+
c
f'(x) = 3a(x-x_j)^2 + 2b(x-x_j) + c
f′(x)=3a(x−xj)2+2b(x−xj)+c
将端点处
f
(
x
j
)
=
y
j
f(x_j) = y_j
f(xj)=yj,
f
(
x
j
+
1
)
=
y
j
+
1
f(x_{j+1}) = y_{j+1}
f(xj+1)=yj+1 带入得
{
f
(
x
j
)
=
d
f
′
(
x
j
)
=
c
f
(
x
j
+
1
)
=
a
(
x
j
+
1
−
x
j
)
3
+
b
(
x
j
+
1
−
x
j
)
2
+
c
(
x
j
+
1
−
x
j
)
f
′
(
x
j
+
1
)
=
3
a
(
x
j
+
1
−
x
j
)
2
+
2
b
(
x
j
+
1
−
x
j
)
+
c
\left\{ \begin{aligned} f(x_j) & = \ d \\ f'(x_j) & = \ c \\ f(x_{j+1}) & = \ a(x_{j+1}-x_j)^3 + b(x_{j+1}- x_j)^2 + c(x_{j+1} - x_j) \\ f'(x_{j+1}) & = \ 3a(x_{j+1}-x_j)^2 + 2b(x_{j+1}- x_j) + c \end{aligned} \right.
⎩
⎨
⎧f(xj)f′(xj)f(xj+1)f′(xj+1)= d= c= a(xj+1−xj)3+b(xj+1−xj)2+c(xj+1−xj)= 3a(xj+1−xj)2+2b(xj+1−xj)+c
可得关于
a
,
b
a,b
a,b 的方程为
{
a
(
x
j
+
1
−
x
j
)
3
+
b
(
x
j
+
1
−
x
j
)
2
=
f
(
x
j
+
1
)
−
f
(
x
j
)
−
f
′
(
x
j
)
−
f
′
(
x
j
)
(
x
j
+
1
−
x
j
)
3
a
(
x
j
+
1
−
x
j
)
2
+
2
b
(
x
j
+
1
−
x
j
)
=
f
′
(
x
j
+
1
)
−
f
′
(
x
j
)
\left\{ \begin{aligned} a(x_{j+1} - x_j)^3 + b(x_{j+1}-x_j)^2 & = f(x_{j+1}) -f(x_j) - f'(x_j)- f'(x_j)(x_{j+1}-x_{j}) \\ 3a(x_{j+1}-x_j)^2 + 2b(x_{j+1} - x_j) & = f'(x_{j+1}) - f'(x_j) \end{aligned} \right.
{a(xj+1−xj)3+b(xj+1−xj)23a(xj+1−xj)2+2b(xj+1−xj)=f(xj+1)−f(xj)−f′(xj)−f′(xj)(xj+1−xj)=f′(xj+1)−f′(xj)
记
x
j
x_j
xj 处的差商
δ
j
=
f
(
x
j
+
1
)
−
f
(
x
j
)
x
j
+
1
−
x
j
\delta_j = \frac{f(x_{j+1}) - f(x_j)}{x_{j+1}-x_j}
δj=xj+1−xjf(xj+1)−f(xj),
x
j
x_j
xj 处的一阶导
d
j
=
f
′
(
x
j
)
d_j = f'(x_j)
dj=f′(xj),
d
z
z
d
x
=
δ
j
−
d
j
x
j
+
1
−
x
j
,
d
z
d
x
d
x
=
d
j
+
1
−
δ
j
x
j
+
1
−
x
j
dzzdx = \frac{δ_j - d_j}{x_{j+1} - x_j},dzdxdx = \frac{d_{j+1} - δ_j}{x_{j+1}-x_{j}}
dzzdx=xj+1−xjδj−dj,dzdxdx=xj+1−xjdj+1−δj,上式可表示为
{
a
(
x
j
+
1
−
x
j
)
+
b
=
d
z
z
d
x
3
a
(
x
j
+
1
−
x
j
)
+
2
b
=
d
z
d
x
d
x
+
d
z
z
d
x
\left\{ \begin{aligned} a(x_{j+1} - x_j) + b & = dzzdx\\ 3a(x_{j+1} - x_j ) +2b & = dzdxdx + dzzdx \end{aligned} \right.
{a(xj+1−xj)+b3a(xj+1−xj)+2b=dzzdx=dzdxdx+dzzdx
解方程组得
{
a
=
d
z
d
x
d
x
−
d
z
z
d
x
x
j
+
1
−
x
j
b
=
2
d
z
z
d
x
−
d
z
d
x
d
x
\left\{ \begin{aligned} a & = \frac{dzdxdx - dzzdx}{x_{j+1} - x_j} \\ b & = 2dzzdx - dzdxdx \end{aligned} \right.
⎩
⎨
⎧ab=xj+1−xjdzdxdx−dzzdx=2dzzdx−dzdxdx
令
h
j
=
x
j
+
1
−
x
j
h_j = x_{j+_1} - x_j
hj=xj+1−xj,最终得出
{
a
=
d
j
+
1
+
d
j
−
2
δ
j
h
j
2
b
=
−
d
j
+
1
−
2
d
j
+
3
δ
j
h
j
c
=
f
′
(
x
j
)
=
d
j
d
=
f
(
x
j
)
=
y
j
\left\{ \begin{aligned} a & = \frac{d_{j+1} + d_j - 2\delta_j}{{h_j} ^2} \\ b & = \frac{-d_{j+1} - 2d_j + 3\delta_j}{h_j} \\ c & = f'(x_j) = d_j \\ d & = f(x_j) = y_j \end{aligned} \right.
⎩
⎨
⎧abcd=hj2dj+1+dj−2δj=hj−dj+1−2dj+3δj=f′(xj)=dj=f(xj)=yj
其中
h
j
、
δ
j
、
y
j
h_j、\delta_j、y_j
hj、δj、yj 均已知,求出
x
j
、
x
j
+
1
x_j、x_{j+1}
xj、xj+1 处的导数
d
j
、
d
j
+
1
d_j、d_{j+1}
dj、dj+1 方程得解
二、一阶导数求法
一、内点处的导数求法
内点处的一阶导数有以下规则:
- 如果第 k k k 个节点附近的差商 δ k − 1 δ_{k-1} δk−1 和 δ k δ_{k} δk 符号相反,或者其中一个为0,则该点处的一阶导数 d k = 0 d_k = 0 dk=0
- 如果第
k
k
k 个节点附近的差商
δ
k
−
1
δ_{k-1}
δk−1 和
δ
k
δ_{k}
δk 符号相同,则改点处的导数
d k + 1 = δ m i n k w 1 k δ k δ m a x k + w 2 k δ k + 1 δ m a x k d_{k+1} = \frac {\delta min_k }{w1_k \frac{\delta_k}{\delta max_k} + w2_k \frac{\delta_{k+1}}{\delta max_k}} dk+1=w1kδmaxkδk+w2kδmaxkδk+1δmink
其中 h k = ( x k + 1 − x k ) , h s k = h k + h k + 1 , δ k = y k + 1 − y k x k + 1 − x k , δ m i n k = m i n ( δ k , δ k + 1 ) , δ m a x k = m a x ( δ k , δ k + 1 ) , w 1 k = h k + h s k 3 h s k , w 2 k = h k + 1 + h s k 3 h s k 其中 h_k = (x_{k+1}-x_k),hs_k = h_k + h_{k+1}, \delta_k = \frac{y_{k+1} - y_k}{x_{k+1} - x_{k}},\delta min_k = min(\delta_{k},\delta_{k+1}),\delta max_k = max(\delta_{k},\delta_{k+1}) ,w1_k = \frac{h_k + hs_k}{3hs_k},w2_k = \frac{h_{k+1} + hs_k}{3hs_k} 其中hk=(xk+1−xk),hsk=hk+hk+1,δk=xk+1−xkyk+1−yk,δmink=min(δk,δk+1),δmaxk=max(δk,δk+1),w1k=3hskhk+hsk,w2k=3hskhk+1+hsk
二、端点处的导数求法
{ d 0 = ( 2 h 0 + h 1 ) δ 0 − h 0 δ 1 ( h 0 + h 1 ) d n = ( 2 h n − 1 + h n − 2 ) δ n − 1 − h n − 1 δ n − 2 ( h n − 2 + h n − 1 ) \left\{ \begin{aligned} d_0 & = \frac{(2h_0 + h_1)\delta_0 - h_0\delta_1}{(h_0+h_1)} \\ d_n & = \frac{(2h_{n-1}+h_{n-2})\delta_{n-1} - h_{n-1}\delta_{n-2}}{(h_{n-2}+h_{n-1})} \end{aligned} \right. ⎩ ⎨ ⎧d0dn=(h0+h1)(2h0+h1)δ0−h0δ1=(hn−2+hn−1)(2hn−1+hn−2)δn−1−hn−1δn−2
二、实验仿真
# -*- encoding: utf-8 -*-
'''
@File : pchip.py
@Time : 2023/03/01 11:40:41
@Author : answer
'''
# here put the import lib
import numpy as np
from matplotlib import pyplot as plt
from scipy import interpolate
def find_0point(delta):
k = []
for i in range(len(delta)-1):
if delta[i] * delta[i+1] > 0:
k.append(i)
return k
# 三次分段hermit函数
def pchip_spline(x, y, frequence):
# x,y差分
x_diff = []
y_diff = []
delta = []
for i in range(len(x)-1):
x_diff.append(x[i+1] - x[i])
y_diff.append(y[i+1] - y[i])
delta.append(y_diff[i]/x_diff[i])
# 节点导数
n = len(x)
slope = [0 for i in range(n)]
if n == 2:
slope = [delta[0] for i in range(n)]
else:
k = find_0point(delta)
for i in range(len(k)):
index = k[i]
dx_diff = x_diff[index] + x_diff[index + 1]
w1 = (x_diff[index] + dx_diff) / (3 * dx_diff)
w2 = (x_diff[index + 1] + dx_diff) / (3 * dx_diff)
dmax = max(abs(delta[index]), abs(delta[index+1]))
dmin = min(abs(delta[index]), abs(delta[index+1]))
slope[index + 1] = dmin / \
(w1*delta[index]/dmax + w2*delta[index+1]/dmax)
slope[0] = 0
# 库函数默认端点导数不为0 interpolate.pchip_interpolate(x, y, x_pchip)
# slope[0] = ((2 * x_diff[0] + x_diff[1]) * delta[0] -
# x_diff[0] * delta[1]) / (x_diff[0] + x_diff[1])
# if slope[0] * delta[0] < 0:
# slope[0] = 0
# elif (delta[0] * delta[1] < 0) & (abs(slope[0]) > 3 * abs(delta[0])):
# slope[0] = 3 * delta[0]
# print(slope)
# slope[n - 1] = ((2 * x_diff[n - 2] + x_diff[n - 3]) * delta[n - 2] -
# x_diff[n - 2] * delta[n - 3]) / (x_diff[n - 3] + x_diff[n - 2])
# if delta[n - 2] * slope[n - 1] < 0:
# slope[n - 1] = 0
# elif (delta[n - 2] * delta[n - 3] < 0) & (abs(slope[n - 1]) > 3 * abs(delta[n - 2])):
# slope[n - 1] = 3 * delta[n - 2]
# print(slope)
# hermit spline
x_hermit = []
y_hermit = []
for i in range(n - 1):
# 计算多项式系数
a = (slope[i + 1] + slope[i] - 2 * delta[i]) / (x_diff[i]**2)
b = (3 * delta[i] - 2 * slope[i] - slope[i + 1]) / x_diff[i]
c = slope[i]
d = y[i]
# 计算插值点
for j in range(frequence):
x_inter = x[i] + j * (x[i+1] - x[i]) / frequence
x_hermit.append(x_inter)
y_hermit.append(
a * (x_inter - x[i])**3 + b * (x_inter - x[i])**2 + c * (x_inter - x[i]) + d)
x_hermit.append(x[n-1])
y_hermit.append(y[n-1])
return x_hermit, y_hermit
if __name__ == '__main__':
frequence = 10
x = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
y = [0, 1.5, 0, 0, 0.5, 0.4, 1.2, 1.2,
0.1, 0, 0.3, 0.6]
x_pchip, y_pchip = pchip_spline(x, y, frequence)
y_ = interpolate.pchip_interpolate(x, y, x_pchip)
y_1 = interpolate.splrep(x, y)
y_1 = interpolate.splev(x_pchip, y_1)
y_2 = interpolate.Akima1DInterpolator(x, y)
y_2 = y_2(x_pchip)
y_3 = interpolate.interp1d(x, y, 'cubic')
y_3 = y_3(x_pchip)
plt.subplot(2, 2, 1)
plt.plot(x, y, "o", label='sample point')
plt.plot(x_pchip, y_, linewidth=3.0, label="scipy_pchip")
plt.plot(x_pchip, y_1, color='lime', label="spline")
plt.legend()
plt.subplot(2, 2, 2)
plt.plot(x, y, "o", label='sample point')
plt.plot(x_pchip, y_, linewidth=3.0, label="scipy_pchip")
plt.plot(x_pchip, y_3, color='blueviolet', label="cubic")
plt.legend()
plt.subplot(2, 2, 3)
plt.plot(x, y, "o", label='sample point')
plt.plot(x_pchip, y_, linewidth=3.0, label="scipy_pchip")
plt.plot(x_pchip, y_2, color='dodgerblue', label="akima")
plt.legend()
plt.subplot(2, 2, 4)
plt.plot(x, y, "o", label='sample point')
plt.plot(x_pchip, y_, linewidth=3.0, label="pchip_scipy")
plt.plot(x_pchip, y_pchip, color='gray', label="pchip d_point=0")
plt.legend()
plt.subplots_adjust(left=0.04, bottom=0.05, right=0.98,
top=0.98, wspace=0.08, hspace=0.1)
plt.show()
-
以 ( 0 , 4 ) , ( 1 , 3 ) , ( 2 , 4 ) , ( 3 , 6 ) , ( 5 , 7 ) , ( 6 , 5 ) , ( 8 , 8 ) , ( 11 , 1 ) (0,4),(1,3),(2,4),(3,6),(5,7),(6,5),(8,8),(11,1) (0,4),(1,3),(2,4),(3,6),(5,7),(6,5),(8,8),(11,1) 作为节点,每点之间插十次
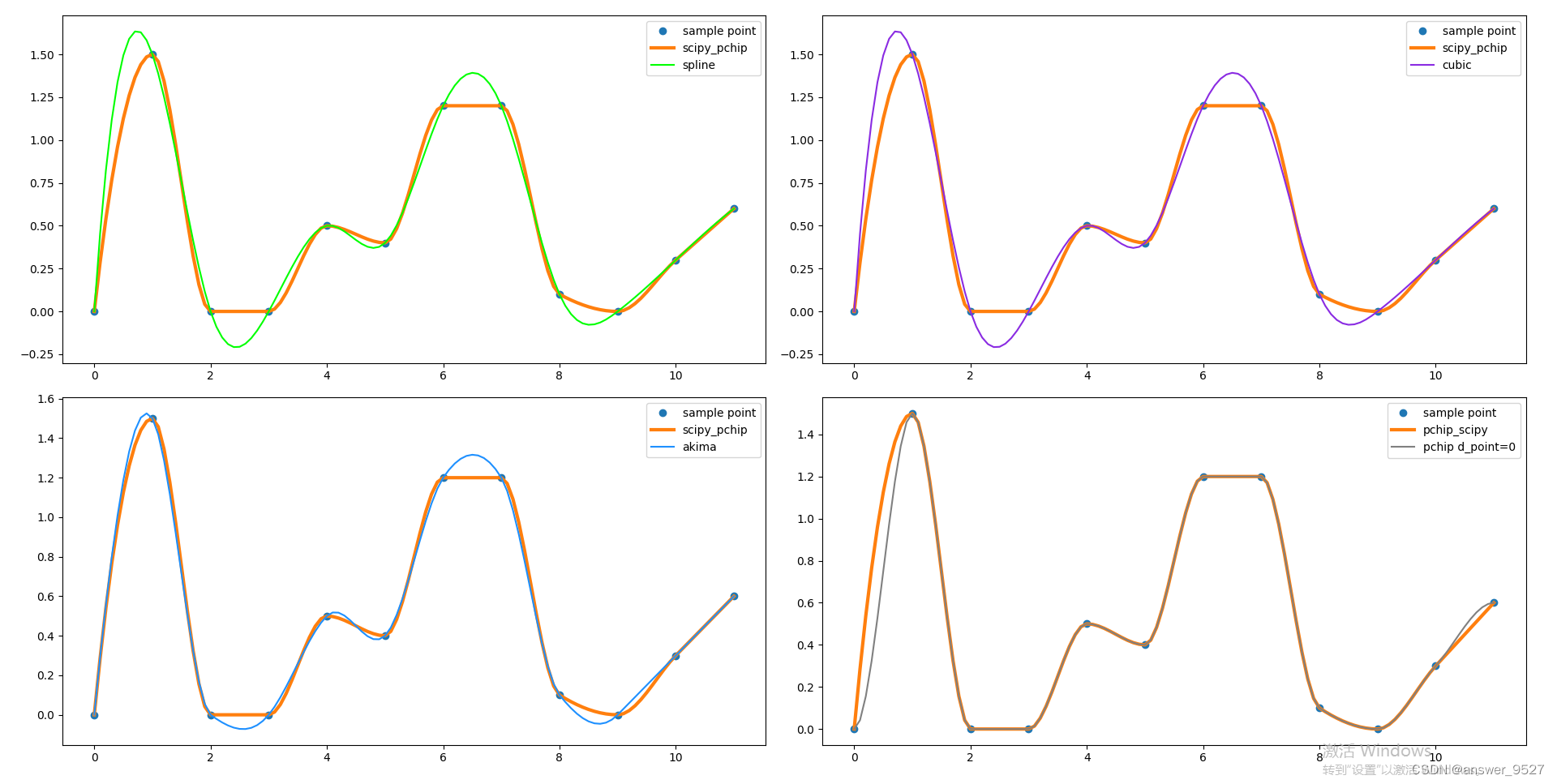
-
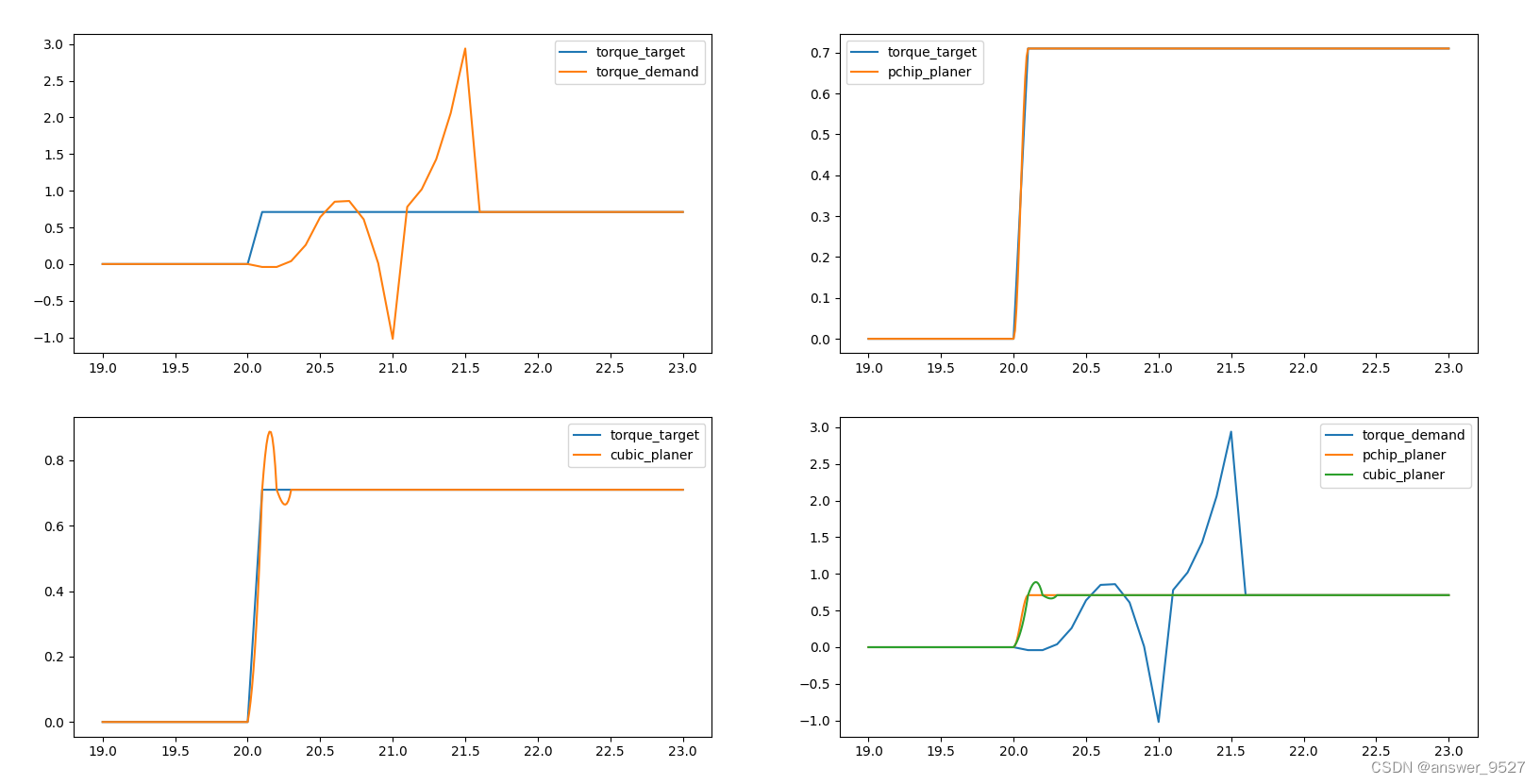
对阶跃信号进行插值