【AI】数学基础——线代(向量部分)
文章目录
- 2.3 矩阵
- 2.3.1 二元方程组求解与行列式
- 行列式
- 2.3.2 用矩阵形式表示数据
- 矩阵与行列式区别
- 特殊矩阵
- 2.3.3 矩阵的秩
- 矩阵的秩
- 2.3.4 矩阵运算
- 加减法
- 数乘运算
- 矩阵乘向量
- 线性变换角度
- 线性组合角度
- 矩阵乘矩阵
- 转置
- 求逆
- 2.4 特征值&特征向量
- 2.4.1 特征值&特征向量
- 2.4.2 特征空间
- 2.5 矩阵分解
- 2.5.1 A = C R A=CR A=CR
- 2.5.2 A = L U A=LU A=LU
- 2.5.3 A = Q R A=QR A=QR
- 2.5.4 特征值分解
- 对称阵的特征值分解
- 2.5.5 SVD
2.3 矩阵
2.3.1 二元方程组求解与行列式
二元方程组求解 { a 11 x 1 + a 12 x 2 = b 1 a 21 x 1 + a 22 x 2 = b 2 \left\{\begin{aligned}a_{11}x_1+a_{12}x_2=b_1\\a_{21}x_1+a_{22}x_2=b_2\end{aligned}\right. {a11x1+a12x2=b1a21x1+a22x2=b2 高斯消元 ⇒ { x 1 = b 1 a 22 − b 2 a 12 a 11 a 22 − a 12 a 21 = ∣ A 1 ∣ ∣ A ∣ x 2 = b 2 a 11 − b 1 a 21 a 11 a 22 − a 12 a 21 = ∣ A 2 ∣ ∣ A ∣ \Rightarrow \left\{\begin{aligned}x_1=\frac{b_1a_{22}-b_2a_{12}}{a_{11}a_{22}-a_{12}a_{21}}=\frac{\vert A_1\vert}{\vert A\vert}\\x_2=\frac{b_2a_{11}-b_1a_{21}}{a_{11}a_{22}-a_{12}a_{21}}=\frac{\vert A_2\vert}{\vert A\vert}\end{aligned}\right. ⇒⎩ ⎨ ⎧x1=a11a22−a12a21b1a22−b2a12=∣A∣∣A1∣x2=a11a22−a12a21b2a11−b1a21=∣A∣∣A2∣
行列式
D
e
t
(
A
)
=
∣
A
∣
Det(A)=\vert A\vert
Det(A)=∣A∣ ,表示面积
∣
a
11
a
12
⋯
a
1
n
a
21
a
22
⋯
a
2
n
⋮
⋮
⋱
⋮
a
n
1
a
n
2
⋯
a
n
n
∣
=
∑
p
1
p
2
⋯
p
n
(
−
1
)
τ
(
p
1
p
2
⋯
p
n
)
a
1
p
1
a
2
p
2
⋯
a
n
p
n
\left\vert \begin{matrix} a_{11}&a_{12}&\cdots&a_{1n}\\ a_{21}&a_{22}&\cdots&a_{2n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n1}&a_{n2}&\cdots&a_{nn} \end{matrix}\right\vert=\sum{p_1p_2\cdots p_n}(-1)^{\tau(p_1p_2\cdots p_n)}a_{1p_1}a_{2p_2}\cdots a_{np_n}
a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann
=∑p1p2⋯pn(−1)τ(p1p2⋯pn)a1p1a2p2⋯anpn
如:
∣
a
b
c
d
∣
=
a
d
−
b
c
\left\vert \begin{matrix}a&b\\c&d\end{matrix}\right\vert=ad-bc
acbd
=ad−bc ,表示平行四边形面积
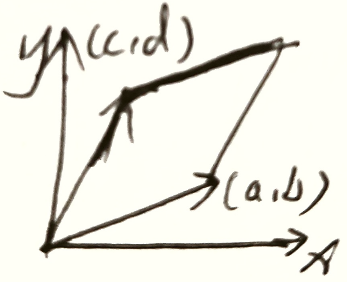
直线可表示为 y = b a x ⟺ b x − a y = 0 y=\frac{b}{a}x\iff bx-ay=0 y=abx⟺bx−ay=0 ,点到直线距离为 ∣ b c − a d ∣ a 2 + b 2 \frac{\vert bc-ad\vert}{\sqrt{a^2+b^2}} a2+b2∣bc−ad∣ 底边长为 a 2 + b 2 \sqrt{a^2+b^2} a2+b2 ,从几何角度,平行四边形面积为 a d − b c ad-bc ad−bc
∣ A ∣ = ∣ a b c d e f g h i ∣ \vert A\vert=\left\vert \begin{matrix}a&b&c\\d&e&f\\g&h&i\end{matrix}\right\vert ∣A∣= adgbehcfi 表示平行六面体体积
2.3.2 用矩阵形式表示数据
四个角度理解矩阵
A = ( a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ) = ( α 1 , α 2 ⋯ , α n ) = ( β 1 β 2 ⋮ β n ) A=\left(\begin{matrix} a_{11}&a_{12}&\cdots&a_{1n}\\ a_{21}&a_{22}&\cdots&a_{2n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{m1}&a_{m2}&\cdots&a_{mn} \end{matrix}\right)=\left(\alpha_1,\alpha_2\cdots,\alpha_n\right)=\left(\begin{aligned}\beta_1\\\beta_2\\\vdots\\\beta_n\end{aligned}\right) A= a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn =(α1,α2⋯,αn)= β1β2⋮βn
用于表示数据 { D = ( X 1 X 2 ⋮ X n ) n 维特征 X i = ( x i 1 , x i 2 , ⋯ , x i n ) 第 i 个数据的 n 维特征值 \left\{\begin{aligned}&D=\left(\begin{aligned}X_1\\X_2\\\vdots\\X_n\end{aligned}\right)&n维特征\\&X_i=(x_{i1},x_{i2},\cdots,x_{in})&第i个数据的n维特征值\end{aligned}\right. ⎩ ⎨ ⎧D= X1X2⋮Xn Xi=(xi1,xi2,⋯,xin)n维特征第i个数据的n维特征值
矩阵由行向量 ( α 1 α 2 ⋮ α n ) \left(\begin{matrix}\alpha_1\\\alpha_2\\\vdots\\\alpha_n\end{matrix}\right) α1α2⋮αn 或列向量 ( α 1 , α 2 , ⋯ , α n ) \left(\alpha_1,\alpha_2,\cdots,\alpha_n\right) (α1,α2,⋯,αn)
矩阵与行列式区别
| 行列式 | 矩阵 |
|---|---|
| 数字 | 阵列 |
| 行列数必须相等 | 行数 ≠ \neq = 列数 |
| 共 n 2 n^2 n2 个元素 | 共 m × n m\times n m×n 个元素 |
| 表示面积(体积) | 表示变换过程 |
特殊矩阵
-
上三角阵
-
下三角阵
-
对角阵 Λ \Lambda Λ
-
单位阵 I I I
-
相等矩阵 ⊂ 同型矩阵 相等矩阵\subset同型矩阵 相等矩阵⊂同型矩阵
相等矩阵必同型,同型矩阵未必相等
-
Jacobian阵
F i = ( ∂ f 1 ∂ x i ∂ f 2 ∂ x i ⋮ ∂ f m ∂ x i ) F_i=\left(\begin{aligned}\frac{\partial f_1}{\partial x_i}\\\frac{\partial f_2}{\partial x_i}\\\vdots\\\frac{\partial f_m}{\partial x_i}\end{aligned}\right) Fi= ∂xi∂f1∂xi∂f2⋮∂xi∂fm ,
J F = ( F 1 , F 2 , ⋯ , F n ) = ( ∂ f 1 ∂ x 1 ∂ f 1 ∂ x 2 ⋯ ∂ f 1 ∂ x n ∂ f 2 ∂ x 1 ∂ f 2 ∂ x 2 ⋯ ∂ f 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ f m ∂ x 1 ∂ f m ∂ x 2 ⋯ ∂ f m ∂ x n ) = [ ▽ f ] i j = [ ∂ f ∂ x j ] i j J_F=\left(F_1,F_2,\cdots,F_n \right)=\left(\begin{matrix}\frac{\partial f_1}{\partial x_1}&\frac{\partial f_1}{\partial x_2}&\cdots&\frac{\partial f_1}{\partial x_n}\\\frac{\partial f_2}{\partial x_1}&\frac{\partial f_2}{\partial x_2}&\cdots&\frac{\partial f_2}{\partial x_n}\\\vdots&\vdots&\ddots&\vdots\\\frac{\partial f_m}{\partial x_1}&\frac{\partial f_m}{\partial x_2}&\cdots&\frac{\partial f_m}{\partial x_n}\end{matrix}\right)=[\bigtriangledown f]_{ij}=\left[\frac{\partial f}{\partial x_j}\right]_{ij} JF=(F1,F2,⋯,Fn)= ∂x1∂f1∂x1∂f2⋮∂x1∂fm∂x2∂f1∂x2∂f2⋮∂x2∂fm⋯⋯⋱⋯∂xn∂f1∂xn∂f2⋮∂xn∂fm =[▽f]ij=[∂xj∂f]ij
J F ′ = ( F 1 , F 2 , ⋯ , F n ) = ( ∂ 2 f 1 ∂ x 1 2 ∂ 2 f 1 ∂ x 1 ∂ x 2 ⋯ ∂ 2 f 1 ∂ x 1 ∂ x n ∂ 2 f 2 ∂ x 1 ∂ x 2 ∂ 2 f 2 ∂ x 2 2 ⋯ ∂ 2 f 2 ∂ x 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ 2 f m ∂ x 1 ∂ x m ∂ 2 f m ∂ x 2 ∂ x m ⋯ ∂ 2 f m ∂ x m ∂ x n ) = [ ▽ 2 f ] i j = [ ∂ 2 f ∂ x i ∂ x j ] i j J_F'=\left(F_1,F_2,\cdots,F_n \right)=\left(\begin{matrix}\frac{\partial^2 f_1}{\partial x_1^2}&\frac{\partial^2 f_1}{\partial x_1\partial x_2}&\cdots&\frac{\partial^2 f_1}{\partial x_1\partial x_n}\\\frac{\partial^2 f_2}{\partial x_1\partial x_2}&\frac{\partial^2 f_2}{\partial x_2^2}&\cdots&\frac{\partial^2 f_2}{\partial x_2\partial x_n}\\\vdots&\vdots&\ddots&\vdots\\\frac{\partial^2 f_m}{\partial x_1\partial x_m}&\frac{\partial^2 f_m}{\partial x_2\partial x_m}&\cdots&\frac{\partial^2 f_m}{\partial x_m\partial x_n}\end{matrix}\right)=[\bigtriangledown^2 f]_{ij}=\left[\frac{\partial^2 f}{\partial x_i\partial x_j}\right]_{ij} JF′=(F1,F2,⋯,Fn)= ∂x12∂2f1∂x1∂x2∂2f2⋮∂x1∂xm∂2fm∂x1∂x2∂2f1∂x22∂2f2⋮∂x2∂xm∂2fm⋯⋯⋱⋯∂x1∂xn∂2f1∂x2∂xn∂2f2⋮∂xm∂xn∂2fm =[▽2f]ij=[∂xi∂xj∂2f]ij
2.3.3 矩阵的秩
有矩阵 A = ( a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a s 1 a s 2 ⋯ a s n ) A=\left(\begin{matrix}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{s1}&a_{s2}&\cdots&a_{sn}\\\end{matrix}\right) A= a11a21⋮as1a12a22⋮as2⋯⋯⋱⋯a1na2n⋮asn
用 n n n 维行向量表示 A = ( α 1 α 2 ⋮ α s ) A=\left(\begin{aligned}\alpha_1\\\alpha_2\\\vdots\\\alpha_s\end{aligned}\right) A= α1α2⋮αs , α i = ( a i 1 , α i 2 , ⋯ , α i n ) \alpha_i=\left(a_{i1},\alpha_{i2},\cdots,\alpha_{in}\right) αi=(ai1,αi2,⋯,αin)
用 s s s 维列向量表示 A = ( β 1 , β 2 , ⋯ , α s ) A=\left(\beta_1,\beta_2,\cdots,\alpha_s\right) A=(β1,β2,⋯,αs) , β i = ( a 1 i a 2 i ⋮ a s i ) \beta_{i}=\left(\begin{aligned}a_{1i}\\a_{2i}\\\vdots\\a_{si}\end{aligned}\right) βi= a1ia2i⋮asi
矩阵的秩
行秩=列秩
r ( A ) = r ( 行向量组 ) = r ( 列向量组 ) r(A)=r(行向量组)=r(列向量组) r(A)=r(行向量组)=r(列向量组)
2.3.4 矩阵运算
有 m × n m\times n m×n 阶矩阵, A = ( a i j ) m × n A=(a_{ij})_{m\times n} A=(aij)m×n , B = ( b i j ) m × n B=(b_{ij})_{m\times n} B=(bij)m×n
加减法
A + B = ( a 11 + b 11 a 12 + b 12 ⋯ a 1 n + b 1 n a 21 + b 21 a 22 + b 22 ⋯ a 2 n + b 2 n ⋮ ⋮ ⋱ ⋮ a n 1 + b n 1 a n 2 + b n 2 ⋯ a n n + b n n ) A+B=\left(\begin{matrix}a_{11}+b_{11}&a_{12}+b_{12}&\cdots&a_{1n}+b_{1n}\\a_{21}+b_{21}&a_{22}+b_{22}&\cdots&a_{2n}+b_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{n1}+b_{n1}&a_{n2}+b_{n2}&\cdots&a_{nn}+b_{nn}\\\end{matrix}\right) A+B= a11+b11a21+b21⋮an1+bn1a12+b12a22+b22⋮an2+bn2⋯⋯⋱⋯a1n+b1na2n+b2n⋮ann+bnn
数乘运算
λ A = A λ = ( λ a 11 λ a 12 ⋯ λ a 1 n λ a 21 λ a 22 ⋯ λ a 2 n ⋮ ⋮ ⋱ ⋮ λ a n 1 λ a n 2 ⋯ λ a n n ) \lambda A=A\lambda=\left(\begin{matrix}\lambda a_{11}&\lambda a_{12}&\cdots&\lambda a_{1n}\\\lambda a_{21}&\lambda a_{22}&\cdots&\lambda a_{2n}\\\vdots&\vdots&\ddots&\vdots\\\lambda a_{n1}&\lambda a_{n2}&\cdots&\lambda a_{nn}\end{matrix}\right) λA=Aλ= λa11λa21⋮λan1λa12λa22⋮λan2⋯⋯⋱⋯λa1nλa2n⋮λann
矩阵乘向量
线性变换角度
1. 对向量进行线性变换
A
X
AX
AX : 对向量X进行线性变换
{
主对角线上元素非零:拉伸
非对角线上元素非零:旋转
\left\{\begin{aligned} 主对角线上元素非零:拉伸\\ 非对角线上元素非零:旋转 \end{aligned}\right.
{主对角线上元素非零:拉伸非对角线上元素非零:旋转
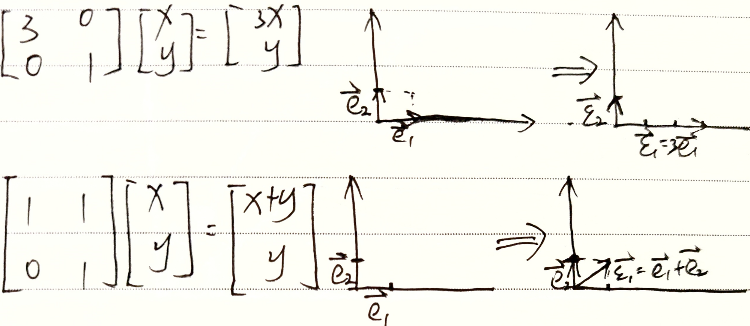
2. 对基进行线性变换
X = I ( x 1 ⋮ x n ) = ( e 1 , ⋯ , e n ) ( x 1 ⋮ x n ) X=I\left(\begin{aligned}x_1\\\vdots\\x_n\end{aligned}\right)=(e_1,\cdots,e_n)\left(\begin{aligned}x_1\\\vdots\\x_n\end{aligned}\right) X=I x1⋮xn =(e1,⋯,en) x1⋮xn
A X = A ( e 1 , ⋯ , e n ) ( x 1 ⋮ x n ) = ( A e 1 , ⋯ , A e n ) ( x 1 ⋮ x n ) AX=A(e_1,\cdots,e_n)\left(\begin{aligned}x_1\\\vdots\\x_n\end{aligned}\right)=(Ae_1,\cdots,Ae_n)\left(\begin{aligned}x_1\\\vdots\\x_n\end{aligned}\right) AX=A(e1,⋯,en) x1⋮xn =(Ae1,⋯,Aen) x1⋮xn
相当于对基进行变换
eg
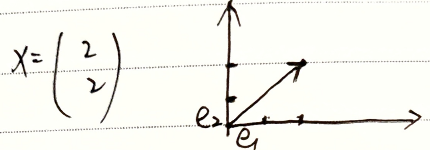
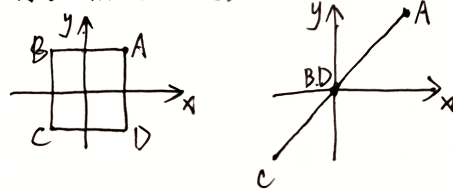
A = ( 3 2 2 3 ) A=\left(\begin{matrix}3&2\\2&3\end{matrix}\right) A=(3223) , X = ( 2 2 ) X=\left(\begin{aligned}2\\2\end{aligned}\right) X=(22)
I X = ( e 1 , e 2 ) ( 2 2 ) = ( 1 0 0 1 ) ( 2 2 ) IX=(e_1,e_2)\left(\begin{aligned}2\\2\end{aligned}\right)=\left(\begin{matrix}1&0\\0&1\end{matrix}\right)\left(\begin{aligned}2\\2\end{aligned}\right) IX=(e1,e2)(22)=(1001)(22) ,如图
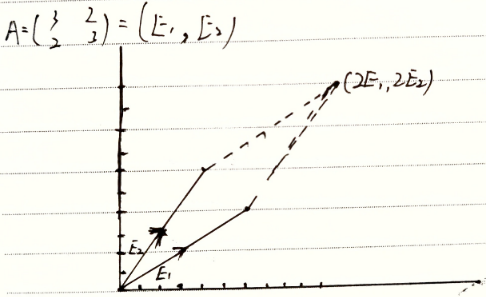
A X = A I X = ( ϵ 1 , ϵ 2 ) ( 2 2 ) = ( 3 2 2 3 ) ( 2 2 ) AX=AIX=\left(\epsilon_1,\epsilon_2\right)\left(\begin{aligned}2\\2\end{aligned}\right)=\left(\begin{matrix}3&2\\2&3\end{matrix}\right)\left(\begin{aligned}2\\2\end{aligned}\right) AX=AIX=(ϵ1,ϵ2)(22)=(3223)(22) 如图
3. 矩阵的秩对变换结果影响
eg1
X = ( a b ) 1 × 2 X=\left(\begin{aligned}a\\b\end{aligned}\right)_{1\times 2} X=(ab)1×2 ,旋转阵 A = [ c o s θ s i n θ − s i n θ cos θ ] A=\left[\begin{matrix}cos\theta &sin\theta\\-sin\theta&\cos\theta\end{matrix}\right] A=[cosθ−sinθsinθcosθ]
A ⋅ X = ( a c o s θ + b s i n θ a c o s θ − b s i n θ ) A\cdot X=\left(\begin{aligned}acos\theta+bsin\theta\\acos\theta-bsin\theta\end{aligned}\right) A⋅X=(acosθ+bsinθacosθ−bsinθ),表示将向量 X X X 旋转 θ \theta θ 度
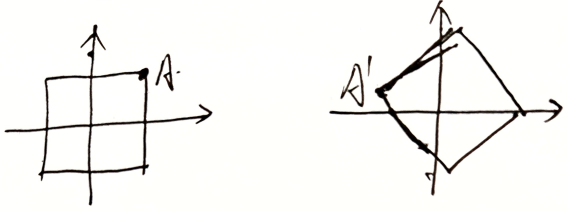
假设 θ = 3 π 2 \theta=\frac{3\pi}{2} θ=23π ,旋转阵 A = [ 0 − 1 1 0 ] A=\left[\begin{matrix}0 &-1\\1&0\end{matrix}\right] A=[01−10] , A X = ( − b a ) AX=\left(\begin{matrix}-b\\a\end{matrix}\right) AX=(−ba)
eg2
若变换阵为 A = [ 1 1 − 1 − 1 ] A=\left[\begin{matrix}1&1\\-1&-1\end{matrix}\right] A=[1−11−1]
变换阵是二维的 r ( A ) = 2 r(A)=2 r(A)=2 ,则对 R n R^n Rn 中所有点变换后也是二维的
变换阵是一维的 r ( A ) = 1 r(A)=1 r(A)=1 ,则对 R n R^n Rn 中所有点变换后也是一维的
线性组合角度
从乘法运算角度, A x Ax Ax 的元素是向量内积
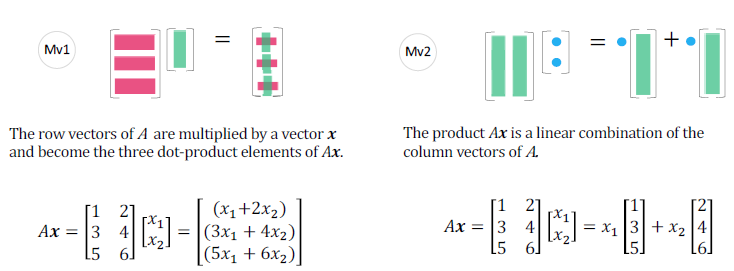
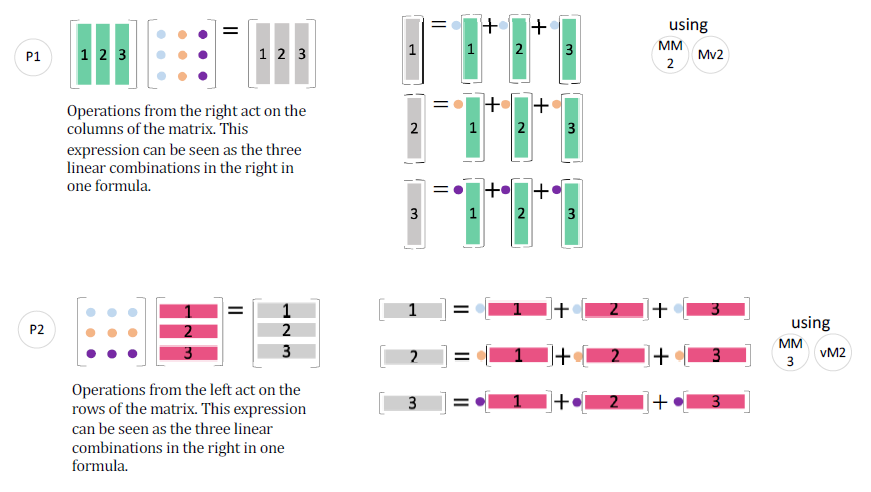
从线性组合角度理解:
A x Ax Ax 是 A A A 的列的线性组合,
- A A A 的列向量的所有线性组合生成的子空间记为 C ( A ) C(A) C(A) ——由 m m m 维列空间组成的秩 r [ C ( A ) ] = r r[C(A)]=r r[C(A)]=r 的空间
- A X = 0 AX=0 AX=0 的解空间则为零空间,记为 N ( A ) N(A) N(A) ——由 n n n 维列向量组成的秩 r [ ( N ( A ) ) ] = n − r r[(N(A))]=n-r r[(N(A))]=n−r 的空间
同理,行向量右乘矩阵
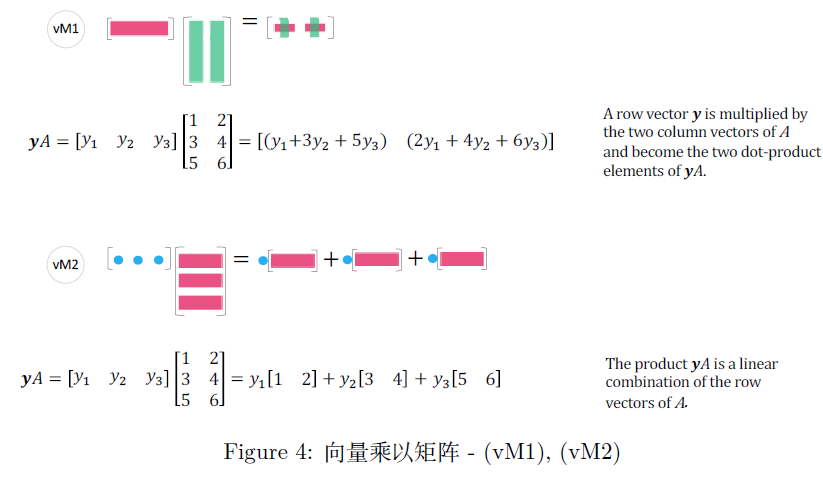
- A A A 的行向量的所有线性组合生成的子空间记为 C ( A T ) C(A^T) C(AT) ——有 n n n 维列向量组成的秩 r [ C ( A T ) ] = r r[C(A^T)]=r r[C(AT)]=r 的空间
- y A = 0 yA=0 yA=0 的解空间是 A A A 的左零空间,记为 N ( A T ) N(A^T) N(AT) ——由 m m m 维列向量组成的秩 r [ N ( A T ) ] = m − r r[N(A^T)]=m-r r[N(AT)]=m−r 的空间
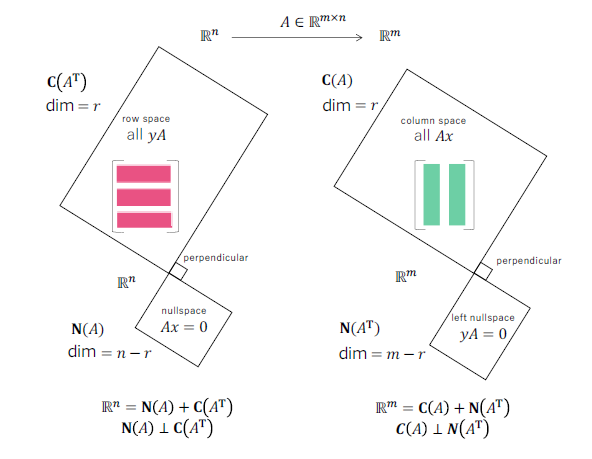
四个基本子空间中 C ( A T ) + N ( A ) = R n C(A^T)+N(A)=\mathbb{R}^n C(AT)+N(A)=Rn , C ( A ) + N ( A T ) ⊂ R m C(A)+N(A^T)\subset\mathbb{R}^m C(A)+N(AT)⊂Rm ,且相互垂直
矩阵乘矩阵
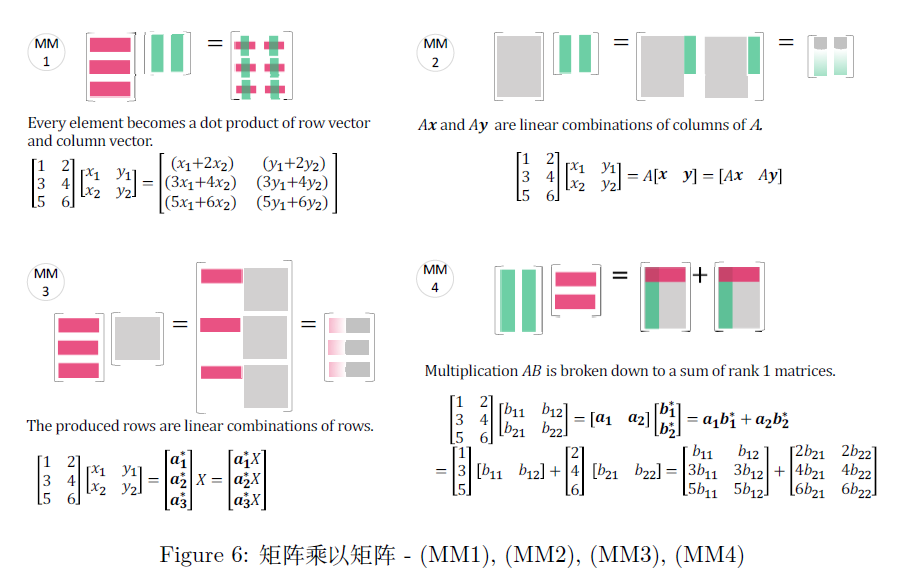
矩阵乘矩阵的每个元素可以理解为向量的内积
也可以理解为矩阵的线性组合(组合系数为向量),进而分割为向量的线性组合
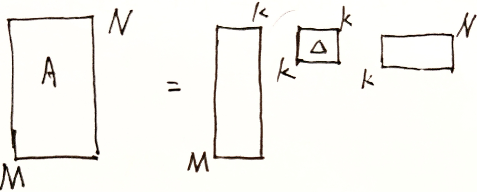
A N × m , B m × n A_{N\times m},B_{m\times n} AN×m,Bm×n ,有 C N × n = A × B , c i j = ∑ k = 1 n a i k b k j , 1 ≤ i ≤ N , 1 ≤ j ≤ n C_{N\times n}=A\times B,c_{ij}=\sum_{k=1}^n a_{ik}b_{kj},1\le i\le N,1\le j\le n CN×n=A×B,cij=∑k=1naikbkj,1≤i≤N,1≤j≤n
eg:
三种商品 B 1 , B 2 , B 3 B_1,B_2,B_3 B1,B2,B3 单价为 B = ( 2.5 3 3.5 ) B=\left(\begin{matrix}2.5\\3\\3.5\end{matrix}\right) B= 2.533.5 ,商场对三种商品销售量分别为 A = ( 12 8 10 14 9 6 ) A=\left(\begin{matrix}12&8&10\\14&9&6\end{matrix}\right) A=(121489106) ,求每个商场营业额
C = A B = ( 12 8 10 14 9 6 ) ( 2.5 3 3.5 ) = ( 12 × 2.5 + 8 × 3 + 10 × 3.5 14 × 2.5 + 9 × 3 + 6 × 3.5 ) = ( 89 83 ) C=AB=\left(\begin{matrix}12&8&10\\14&9&6\end{matrix}\right)\left(\begin{matrix}2.5\\3\\3.5\end{matrix}\right)=\left(\begin{matrix}12\times 2.5+8\times 3+10\times 3.5\\14\times 2.5+9\times 3+6\times 3.5\end{matrix}\right)=\left(\begin{matrix}89\\83\end{matrix}\right) C=AB=(121489106) 2.533.5 =(12×2.5+8×3+10×3.514×2.5+9×3+6×3.5)=(8983)
性质
- 无交换律: A B ≠ B A AB\neq BA AB=BA
- 结合律: ( A B ) C = A ( B C ) (AB)C=A(BC) (AB)C=A(BC)
- 分配律: A ( B + C ) = A B + A C A(B+C)=AB+AC A(B+C)=AB+AC , ( B + C ) A = B A + C A (B+C)A=BA+CA (B+C)A=BA+CA
特殊的矩阵乘法
矩阵乘对角阵


在解决微分方程和递归方程时会出现这 X D c XDc XDc 模式
( 1 ) d u ( t ) d t = A u ( t ) , u ( 0 ) = u 0 (1)\quad\frac{du(t)}{dt}=Au(t),u(0)=u_0 (1)dtdu(t)=Au(t),u(0)=u0
( 2 ) u n + 1 = A u n , u 0 = u 0 (2)\quad u_{n+1}=Au_n,u_0=u_0 (2)un+1=Aun,u0=u0
解这两种情况的解都可以用 A A A 的特征值 ( λ 1 , λ 2 , λ 3 ) \left(\lambda_1,\lambda_2,\lambda_3\right) (λ1,λ2,λ3) ,特征向量 X = [ x 1 , x 2 , x 3 ] X=[x_1,x_2,x_3] X=[x1,x2,x3] 和系数 c = ( c 1 c 2 c 3 ) c=\left(\begin{aligned}c_1\\c_2\\c_3\end{aligned}\right) c= c1c2c3 表示,其中 c c c 是以 X X X 为基底的初始值 u ( 0 ) = u 0 u(0)=u_0 u(0)=u0 的坐标
u 0 = c 1 x 1 + c 2 x 2 + c 3 x 3 = [ x 1 , x 2 , x 3 ] ( c 1 c 2 c 3 ) = X c u_0=c_1x_1+c_2x_2+c_3x_3=\left[x_1,x_2,x_3\right]\left(\begin{aligned}c_1\\c_2\\c_3\end{aligned}\right)=Xc u0=c1x1+c2x2+c3x3=[x1,x2,x3] c1c2c3 =Xc
c = ( c 1 c 2 c 3 ) = X − 1 u 0 c=\left(\begin{aligned}c_1\\c_2\\c_3\end{aligned}\right)=X^{-1}u_0 c= c1c2c3 =X−1u0
对于 ( 1 ) ( 2 ) (1)(2) (1)(2) 的通解表示为:
u ( t ) = e A t u 0 = X e Λ t X − 1 u 0 = X e Λ t c = c 1 e λ 1 t x 1 + c 2 e λ 2 t x 2 + c 3 e λ 3 t x 3 u(t)=e^{At}u_0=Xe^{\Lambda t}X^{-1}u_0=Xe^{\Lambda t}c=c_1e^{\lambda_1t}x_1+c_2e^{\lambda_2t}x_2+c_3e^{\lambda_3t}x_3 u(t)=eAtu0=XeΛtX−1u0=XeΛtc=c1eλ1tx1+c2eλ2tx2+c3eλ3tx3
u n = A n u 0 = X Λ n X − 1 u 0 = X Λ n c = c 1 λ 1 n x 1 + c 2 λ 2 n x 2 + c 3 λ 3 n x 3 u_n=A^{n}u_0=X\Lambda^nX^{-1}u_0=X\Lambda^nc=c_1\lambda_1^nx_1+c_2\lambda_2^nx_2+c_3\lambda_3^nx_3 un=Anu0=XΛnX−1u0=XΛnc=c1λ1nx1+c2λ2nx2+c3λ3nx3
转置
A = ( a 11 a 12 a 21 a 22 ) A=\left(\begin{matrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{matrix}\right) A=(a11a21a12a22) , A T = ( a 11 a 21 a 12 a 22 ) A^T=\left(\begin{matrix}a_{11}&a_{21}\\a_{12}&a_{22}\end{matrix}\right) AT=(a11a12a21a22)
性质
- ( A T ) T = A (A^T)^T=A (AT)T=A
- ( A + B ) T = A T + B T (A+B)^T=A^T+B^T (A+B)T=AT+BT
- ( A B ) T = B T A T (AB)^T=B^TA^T (AB)T=BTAT
- ( λ A ) T = λ A T (\lambda A)^T=\lambda A^T (λA)T=λAT
若 A A A 为对称阵,则 A = A T A=A^T A=AT ;对角线上元素为实数
求逆
若有 B A = A B = I BA=AB=I BA=AB=I ,则有 A − 1 = B , B − 1 = A A^{-1}=B,B^{-1}=A A−1=B,B−1=A
性质
若 A A A 与 B B B 可逆,则有
- ( A − 1 ) − 1 = A (A^{-1})^{-1}=A (A−1)−1=A
- ( A B ) − 1 = B − 1 A − 1 (AB)^{-1}=B^{-1}A^{-1} (AB)−1=B−1A−1
- ( A T ) − 1 = ( A − 1 ) T (A^T)^{-1}=(A^{-1})^T (AT)−1=(A−1)T
- ( λ A ) − 1 = 1 λ A − 1 (\lambda A)^{-1}=\frac{1}{\lambda}A^{-1} (λA)−1=λ1A−1
2.4 特征值&特征向量
2.4.1 特征值&特征向量
A X = λ X ( X ≠ 0 ) AX=\lambda X(X\neq 0) AX=λX(X=0) :经变换后方向不变的向量(特征向量),在方向上有伸缩量 λ \lambda λ (特征值)
eg
A = ( 1 2 0 3 ) A=\left(\begin{matrix}1&2\\0&3\end{matrix}\right) A=(1023) , X = ( 1 1 ) X=\left(\begin{aligned}1\\1\end{aligned}\right) X=(11)
A X = ( 1 2 0 3 ) ( 1 1 ) = 3 ( 1 1 ) AX=\left(\begin{matrix}1&2\\0&3\end{matrix}\right)\left(\begin{aligned}1\\1\end{aligned}\right)=3\left(\begin{aligned}1\\1\end{aligned}\right) AX=(1023)(11)=3(11)
2.4.2 特征空间
特征空间包含了所有特征向量
λ \lambda λ 越大表示相应的特征向量越重要,在降维或压缩时尽量保存
2.5 矩阵分解
五种重要的矩阵分解
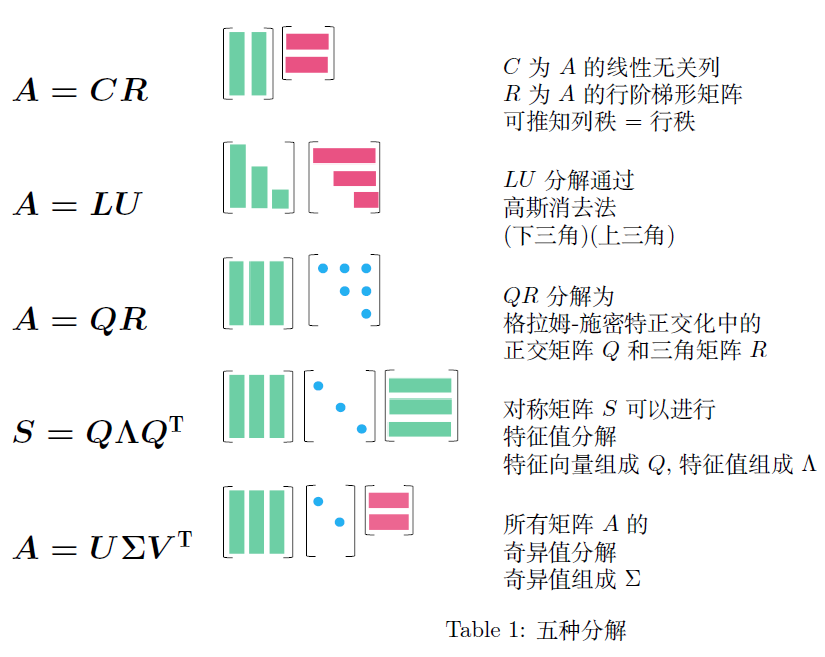
2.5.1 A = C R A=CR A=CR
所有的长矩阵 A A A 都有相同的行秩和列秩。 C C C 由 A A A 中线性无关的列组成, R R R 为 A A A 的行阶梯阵。即将 A A A 化简为 r r r 的线性无关列 C C C 和线性无关行 R R R 的乘积
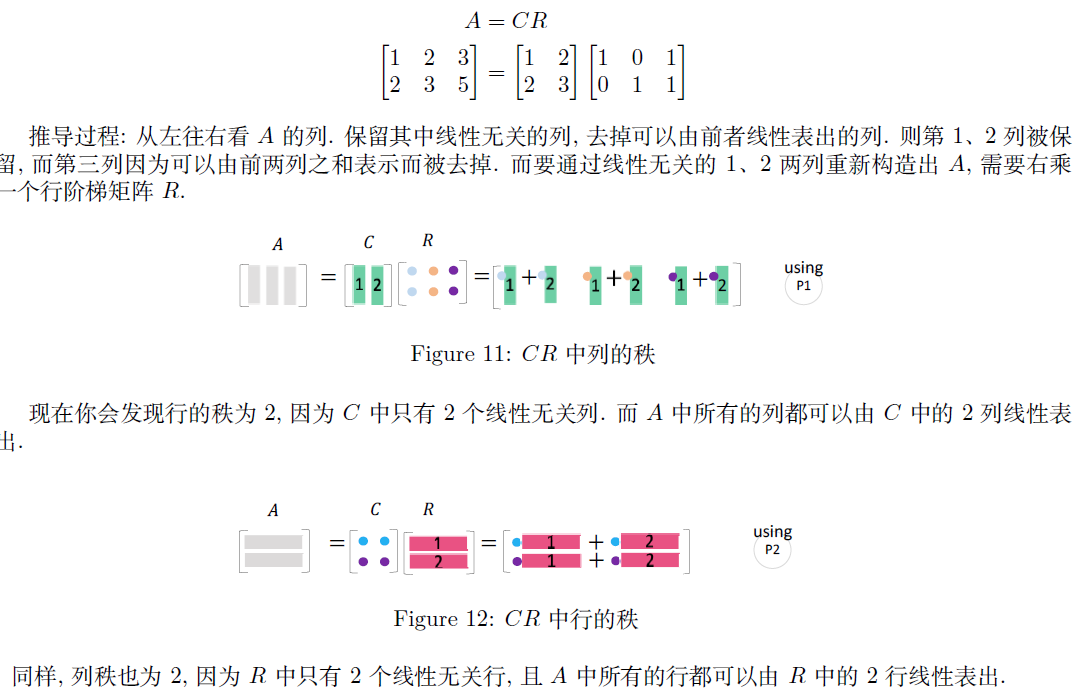
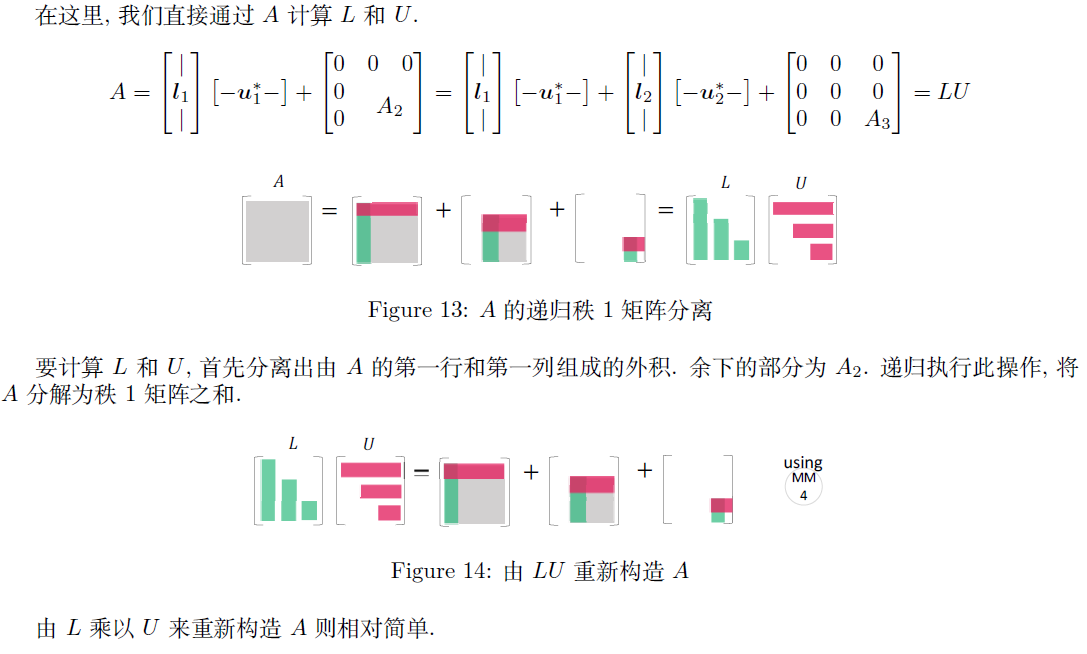
2.5.2 A = L U A=LU A=LU
高低分解
通常是
A
A
A 左乘一个初等行变换阵
E
E
E 来得到一个上三角阵
U
U
U
E
A
=
U
A
=
E
−
1
U
令
L
−
1
=
E
−
1
,
A
=
L
U
EA=U\\ A=E^{-1}U\\ 令 L^{-1}=E^{-1} ,A=LU
EA=UA=E−1U令L−1=E−1,A=LU
2.5.3 A = Q R A=QR A=QR
Q R QR QR 分解是在保持 C ( A ) = C ( Q ) C(A)=C(Q) C(A)=C(Q) 的条件下,将 A A A 转化为正交矩阵 Q Q Q
在施密特正交化中,单位化的 a 1 a_1 a1 被用作 q 1 q_1 q1 ,然后求出 a 2 a_2 a2 与 q 1 q_1 q1 正交所得到的 q 2 q_2 q2 ,以此类推
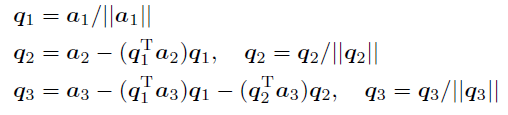

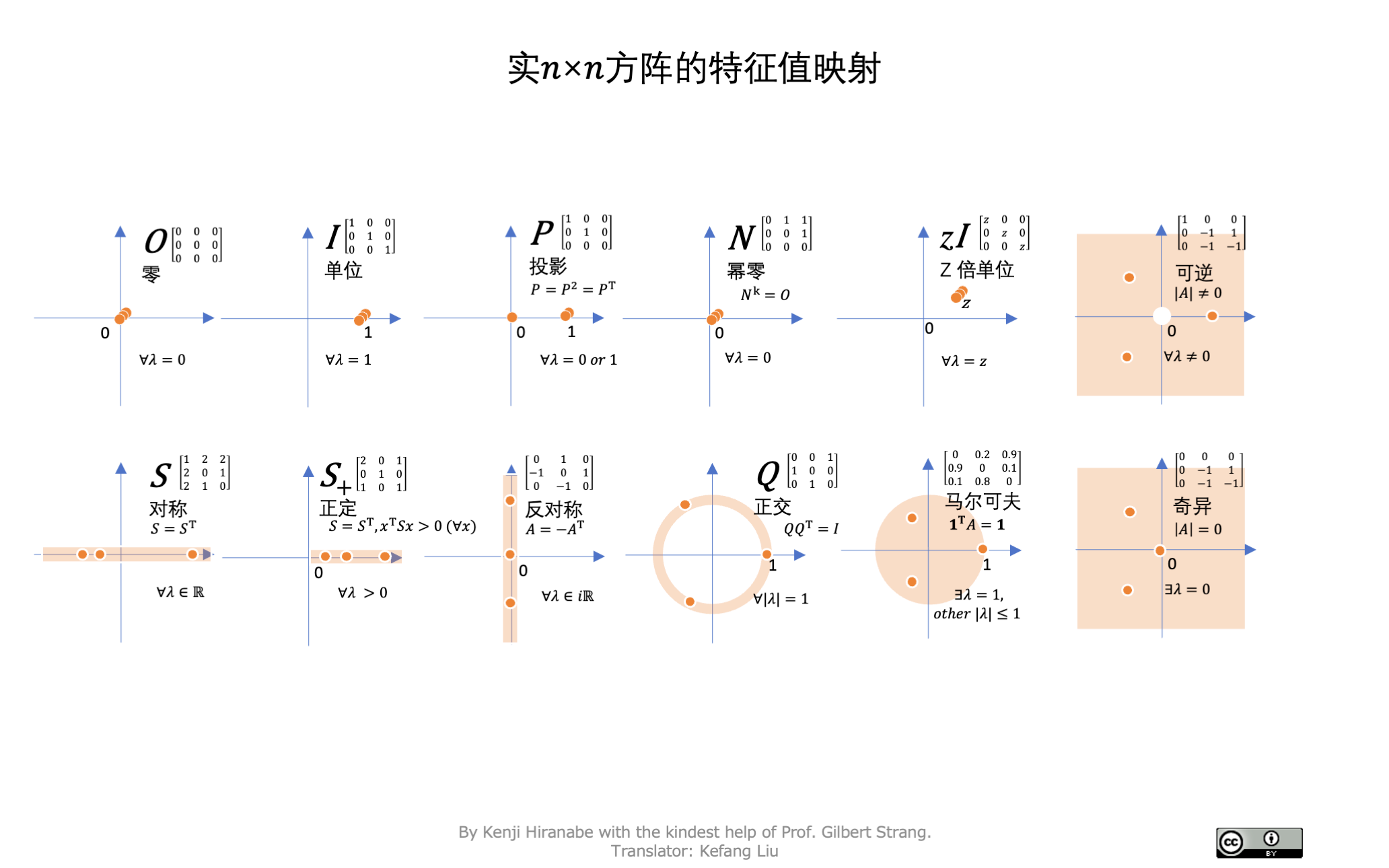
2.5.4 特征值分解
方阵 A A A 可相似对角化, P − 1 A P = Λ = ( λ 1 λ 2 ⋱ λ n ) P^{-1}AP=\Lambda=\left(\begin{matrix}\lambda_1&&&\\&\lambda_2\\&&\ddots\\&&&\lambda_n\end{matrix}\right) P−1AP=Λ= λ1λ2⋱λn ,则 P P P 中为特征向量
条件: A A A 为 n × n n\times n n×n 阶方阵, A A A 有 n n n 个线性无关的特征向量
作用:便于在 n n n 个特征值中找到 k k k 个较大的特根,用于代替方阵 A A A
对称阵的特征值分解
所有对称矩阵 S S S 都必有实特征值和正交特征向量。特征值是 Λ \Lambda Λ 的对角元素,特征向量在 Q Q Q 中
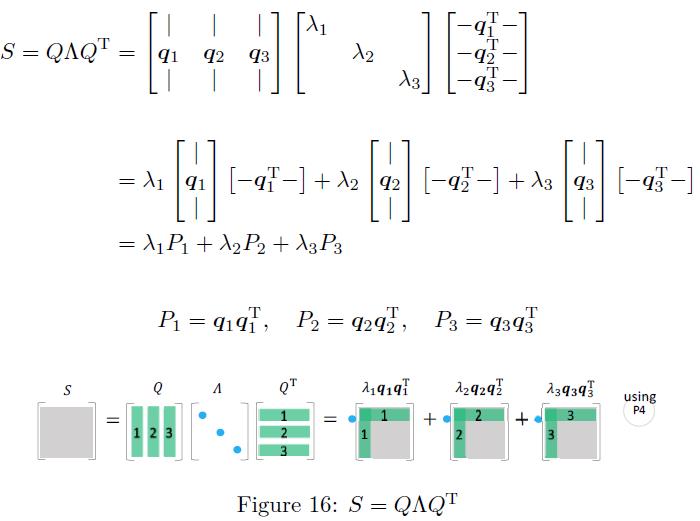
一个对称阵 S S S 通过一个正交矩阵 Q Q Q 和 Q T Q^T QT ,对角化为 Λ \Lambda Λ 。然后被分解为一阶投影矩阵 P = q q T P=qq^T P=qqT 的组合,就是谱定理
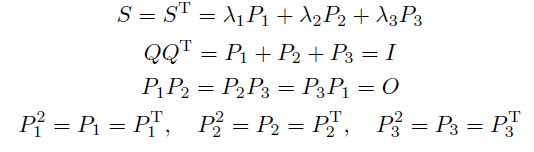
2.5.5 SVD
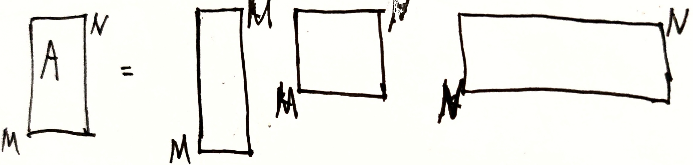
故筛选出 k k k 个比较大的特征值, SVD分解为选出所有正奇值
λ ( A H A ) = { λ 1 , λ 2 , ⋯ , λ n } \lambda(A^HA)=\{\lambda_1,\lambda_2,\cdots,\lambda_n\} λ(AHA)={λ1,λ2,⋯,λn} 中 λ 1 , ⋯ , λ k > 0 \lambda_1,\cdots,\lambda_k>0 λ1,⋯,λk>0 ,故取 s 1 + = λ 1 , s 2 + = λ 2 , ⋯ , s k + λ k s_1^+=\sqrt{\lambda_1},s_2^+=\sqrt{\lambda_2},\cdots,s_k^+\sqrt{\lambda_k} s1+=λ1,s2+=λ2,⋯,sk+λk 为正奇值代替代替矩阵 A A A