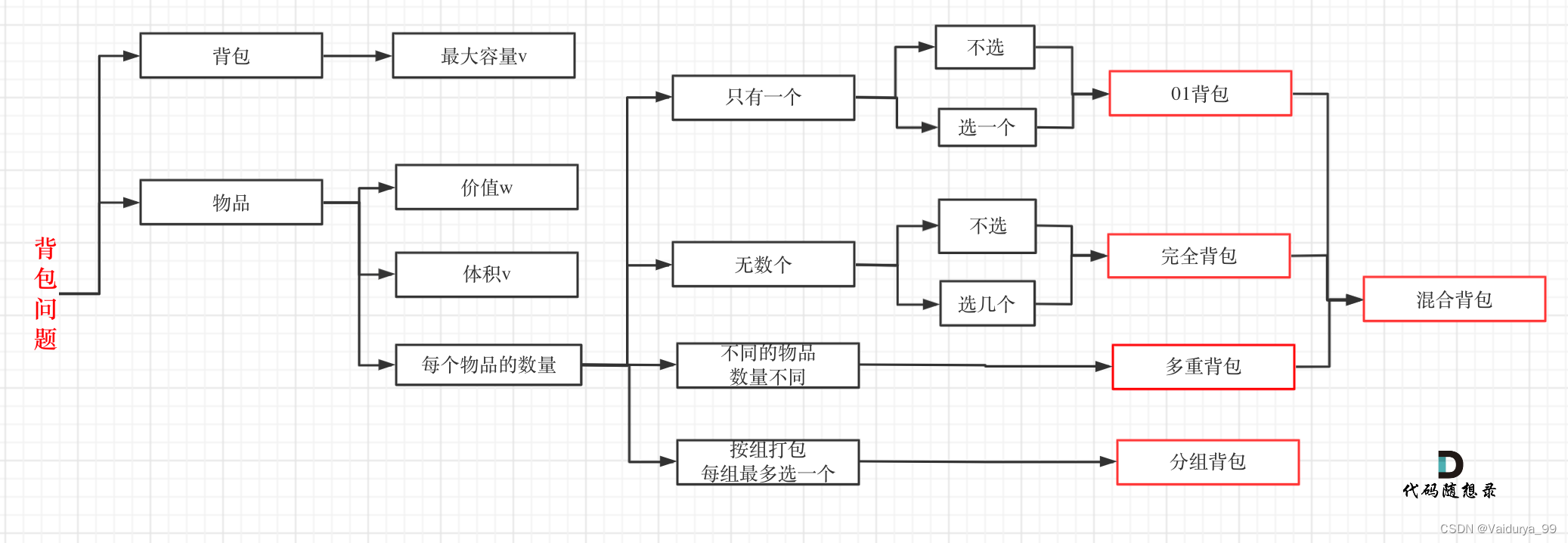
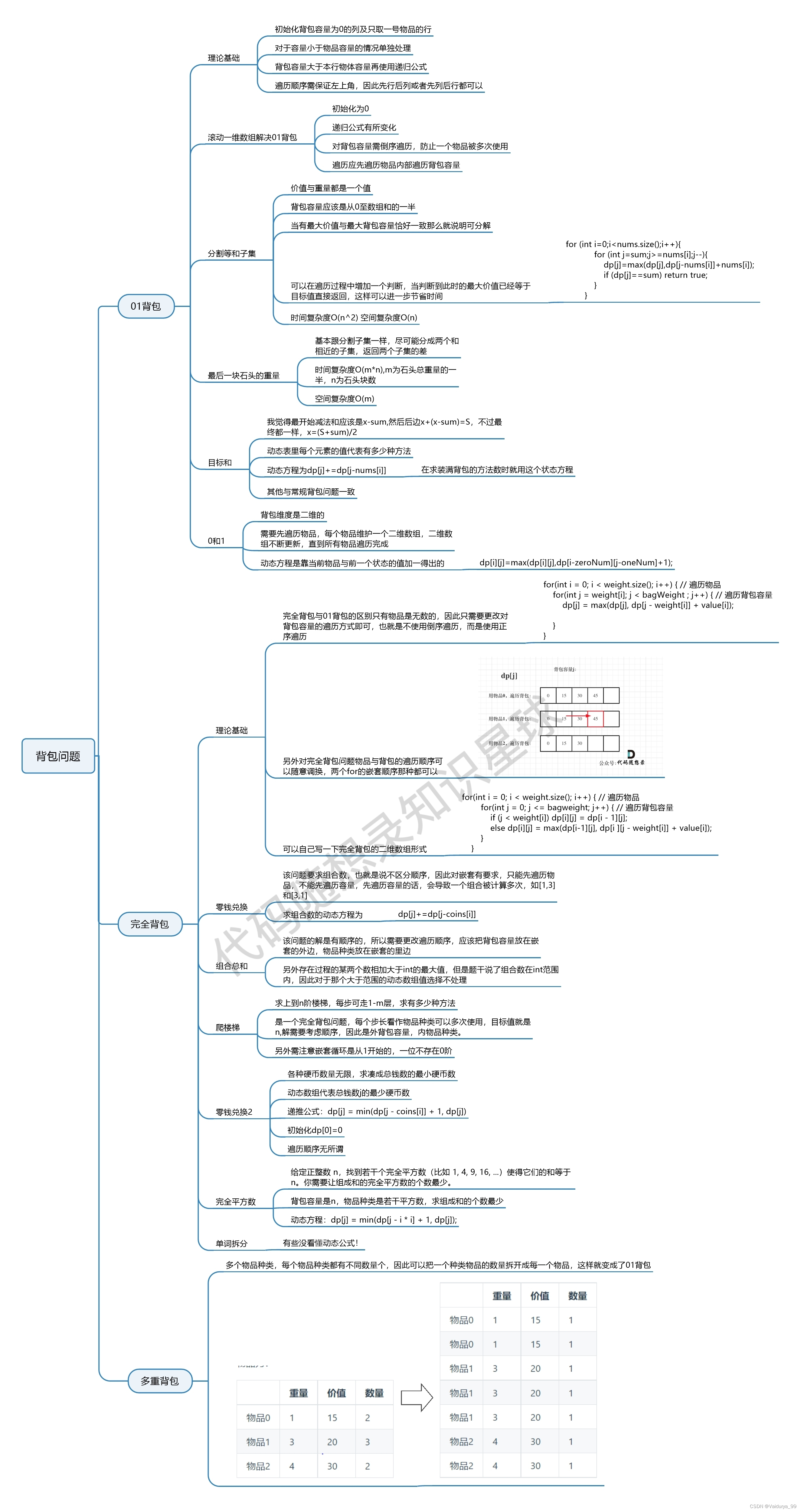
1 139. 单词拆分

139. 单词拆分

做了很久...估计2h 一开始我的思路卡死了 + 看题解之后的思路的详解见注释，

我的写法和carl 答案在一些微小的细节上略有不同，我的更好理解，但他的解法更简单。

我写的过程中，需要注意下标和字符串大小的关系要不要+1-1，而且dp[] 需要从1开始到n有意义，dp[0] 不管它。不可以只有0,...,n-1 这样会忽略s = "a" Dict = ["b"] 这样的样例，因为dp[0] 恒为1。

AC代码：

class Solution {
public:
    //多重背包且排列
    /*
        一开始我的思路——
        物品:字典里面str
        背包:容量为？的背包  求装满时候的情况
         dp[wordDict.size()][s.size()]
        如果n = wordDict.size() m = s.size()  又感觉要考虑每个字符和Dict中每个字符串的关系 很麻烦        
    */

    /*
        看了题解，才知道我纠结的地方 每个字符和Dict中每个字符串的关系 很麻烦，但其实可以用substr函数考虑背包的s的子串和Dict中每个字符串来比较，这样就变得很简单了。
        而且之前思考时候不知道dp[]存的值要是int还是char什么东西
        其实就题目结果反推，dp[] = trur/flase
    */
    bool dp[310];   //以i结尾的字符串是否可以利用字典中出现的单词拼接出来
    /*
        dp[j] = dp[j - wordDict[i].size()] && substr(s,j - wordDict[i].size(),wordDict[i].size()) == wordDict[i];

        dp[0] = 1;

        多重背包+排列
        背包j++ 物体i++

        模拟——
        6 7 8 9 10 11
        j = 11 size = 5 dp[6]
    */

    bool wordBreak(string s, vector<string>& wordDict) {
        dp[0] = 1;
        bool tmp[100][100];

        for(int j = 0; j <= s.size();j++)
        {
            for(int i = 0; i　< wordDict.size();i++)
            {
                if(j == wordDict[i].size())  // 能装下一个
                    dp[j] =  (s.substr(j  - wordDict[i].size(),wordDict[i].size()) == wordDict[i]) || dp[j];

                else if(j > wordDict[i].size() )    // 能至少装2个 
                    dp[j] = dp[j  - wordDict[i].size()] && (s.substr(j - wordDict[i].size(),wordDict[i].size()) == wordDict[i]) || dp[j];

            }
        }

        // for(int i = 0; i　< wordDict.size();i++)
        // {
        //     for(int j = 0; j < s.size();j++)
        //         cout << tmp[i][j] << ' ';
        //     cout << endl;
        // }
        
        return dp[s.size() ];
    }
};