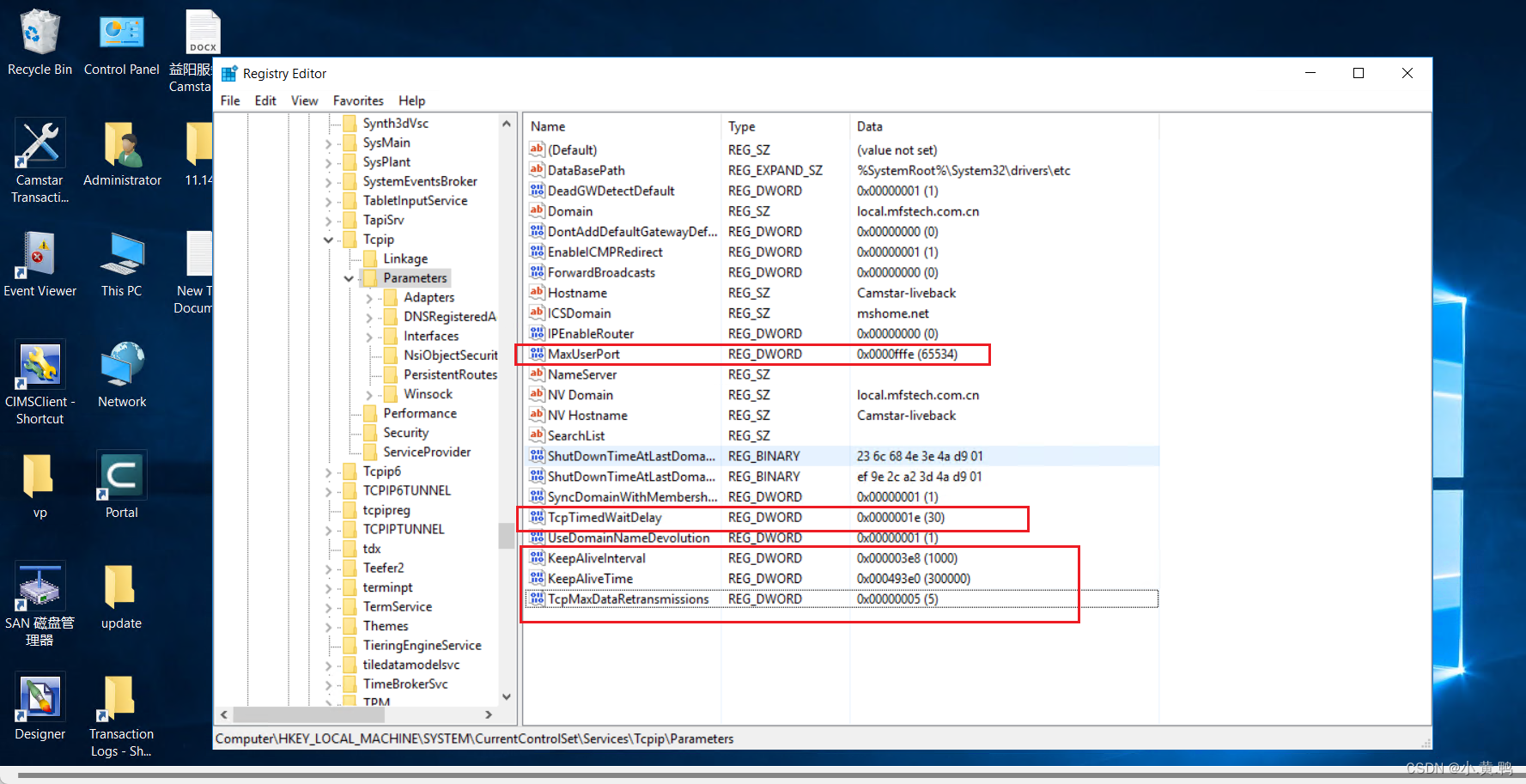
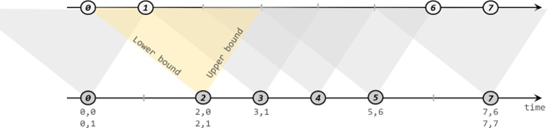
1 文本格式

using System;

namespace Legalsoft.Truffer
{
    /// <summary>
    ///  Structure for implementing the DE (double exponential) rule.
    /// </summary>
    public class DErule : Quadrature
    {
        private double a { get; set; }
        private double b { get; set; }
        private double hmax { get; set; }
        private double s { get; set; }

        public DErule(RealValueFun funcc, double aa, double bb, double hmaxx = 3.7)
        {
            this.func = funcc;
            this.a = aa;
            this.b = bb;
            this.hmax = hmaxx;
            n = 0;
        }

        /// <summary>
        /// On the first call to the function next(n D 1), the routine returns the
        /// crudest estimate of S(a, b)f(x)dx..Subsequent calls to next(n = 2,3,...)
        /// will improve the accuracy by adding 2^(n-1) additional interior points.
        /// </summary>
        /// <returns></returns>
        public override double next()
        {
            double fact;
            n++;
            if (n == 1)
            {
                fact = 0.25;
                return s = hmax * 2.0 * (b - a) * fact * func.funk(new double[] { 0.5 * (b + a), 0.5 * (b - a) });
            }
            else
            {
                int it = 1;
                for (int j = 1; j < n - 1; j++)
                {
                    it <<= 1;
                }
                double twoh = hmax / it;
                double t = 0.5 * twoh;
                double sum = 0.0;
                for (int j = 0; j < it; j++)
                {
                    double q = Math.Exp(-2.0 * Math.Sinh(t));
                    double del = (b - a) * q / (1.0 + q);
                    fact = q / Globals.SQR(1.0 + q) * Math.Cosh(t);
                    sum += fact * (func.funk(new double[] { a + del, del }) + func.funk(new double[] { b - del, del }));
                    t += twoh;
                }
                return s = 0.5 * s + (b - a) * twoh * sum;
            }
        }
    }
}

2 代码格式

using System;

namespace Legalsoft.Truffer
{
    /// <summary>
    ///  Structure for implementing the DE (double exponential) rule.
    /// </summary>
    public class DErule : Quadrature
    {
        private double a { get; set; }
        private double b { get; set; }
        private double hmax { get; set; }
        private double s { get; set; }

        public DErule(RealValueFun funcc, double aa, double bb, double hmaxx = 3.7)
        {
            this.func = funcc;
            this.a = aa;
            this.b = bb;
            this.hmax = hmaxx;
            n = 0;
        }

        /// <summary>
        /// On the first call to the function next(n D 1), the routine returns the
        /// crudest estimate of S(a, b)f(x)dx..Subsequent calls to next(n = 2,3,...)
        /// will improve the accuracy by adding 2^(n-1) additional interior points.
        /// </summary>
        /// <returns></returns>
        public override double next()
        {
            double fact;
            n++;
            if (n == 1)
            {
                fact = 0.25;
                return s = hmax * 2.0 * (b - a) * fact * func.funk(new double[] { 0.5 * (b + a), 0.5 * (b - a) });
            }
            else
            {
                int it = 1;
                for (int j = 1; j < n - 1; j++)
                {
                    it <<= 1;
                }
                double twoh = hmax / it;
                double t = 0.5 * twoh;
                double sum = 0.0;
                for (int j = 0; j < it; j++)
                {
                    double q = Math.Exp(-2.0 * Math.Sinh(t));
                    double del = (b - a) * q / (1.0 + q);
                    fact = q / Globals.SQR(1.0 + q) * Math.Cosh(t);
                    sum += fact * (func.funk(new double[] { a + del, del }) + func.funk(new double[] { b - del, del }));
                    t += twoh;
                }
                return s = 0.5 * s + (b - a) * twoh * sum;
            }
        }
    }
}