复数的四则运算（java版）

介绍

• 复数，为实数的延伸，它使任一多项式方程都有根。复数当中有个“虚数单位 ” i，它是−1的一个平方根，即 i^2=−1。任一复数都可表达为 **x+yi，**其中x及y皆为实数，分别称为复数之“实部”和“虚部”。

• 四则运算，是一种简单基本的数学运算，即 加法 、 减法 、 乘法 和 除法 四种运算。

复数的四则运算

要想实现复数的四则运算，我们就要先知道复数的四则运算分别都是如何计算的。

两个复数的四则运算（数学表达式）

复数一：a+bi  
复数二：c+di

加法 a+bi + c+di = (a+c)+(b+d)i
减法 a+bi - (c+di) = (a-c)+(b+d)i
乘法 a+bi * (c+di) = (ac-bd) + (ad+bc)i
除法 (a+bi)/(c+di) = [(ac+bd)+(bc-ad)i]/(c^2+d^2)

实现思路

由于 java程序设计语言 是一门面向对象编程的，所以我们可以考虑把 复数 封装成一个类，然后我们就可以实例化这个类，创建 复数 对象。我们在封装这个类的时候就可以思考该怎么封装，要去思考 复数 这个对象 中应该具备什么样的属性和特征。

• 状态特征

状态特征也就是 复数对象 拥有的属性，应该有 实部 和 虚部

• 行为特征

行为特征也就是 复数对象 的具备方法，除了构造和setter and getter 方法，还应该有 实现复数相加的方法add()，实现复数相减的方法sub(),实现 复数相乘的方法mul(),实现复数相除的除法div()，还有重写toString()的方法。

代码

1、封装复数类

//复数的四则运算
public class Complex {
        //实部和虚部的定义
        //定义成double比较好的的原因之一是因为 有除法运算
        private double realPart;
        private double imagePart;

        //构造方法
        public Complex() {

        }

        public Complex(double realPart, double imagePart) {
            this.realPart = realPart;
            this.imagePart = imagePart;
        }
    
        //setter and getter
        public double getImagePart() {
            return imagePart;
        }

        public void setImagePart(double imagePart) {
            this.imagePart = imagePart;
        }

        public double getRealPart() {
            return realPart;
        }

        public void setRealPart(double realPart) {
            this.realPart = realPart;
        }

        //复数的加法
        public Complex add(Complex complexNumber) {
            if (complexNumber == null) {
                System.out.println("复数对象输入错误");
                return new Complex();
            }
            double newImagePart = this.getImagePart() + complexNumber.getImagePart();
            double newRealPart = this.getRealPart() + complexNumber.getRealPart();
            return new Complex(newRealPart, newImagePart);
        }

        //复数的减法
        public Complex sub(Complex complexNumber) {
            if (complexNumber == null) {
                System.out.println("复数对象输入错误");
                return new Complex();
            }
            double newImagePart = this.getImagePart() - complexNumber.getImagePart();
            double newRealPart = this.getRealPart() - complexNumber.getRealPart();
            return new Complex(newRealPart, newImagePart);
        }

        //复数的乘法
        public Complex mul(Complex complexNumber) {
            if (complexNumber == null) {
                System.out.println("输入复数对象错误");
                return new Complex();
            }
            double newRealPart = this.getRealPart() * complexNumber.getRealPart() - this.getImagePart() * complexNumber.getImagePart();
            double newImagePart = this.getRealPart() * complexNumber.getImagePart() + this.getImagePart() * complexNumber.getRealPart();
            return new Complex(newRealPart, newImagePart);
        }

        public Complex division(Complex complexNumber) {
            if (complexNumber == null) {
                System.out.println("输入复数对象错误");
                return new Complex();
            }
            double newRealPart = (this.getRealPart() * complexNumber.getRealPart() + this.getImagePart() * complexNumber.getImagePart()) / (complexNumber.getRealPart() * complexNumber.getRealPart() + complexNumber.getImagePart() * complexNumber.getImagePart());
            double newImagePart = (-this.getRealPart() * complexNumber.getImagePart() + this.getImagePart() * complexNumber.getRealPart())/ (complexNumber.getRealPart() * complexNumber.getRealPart() + complexNumber.getImagePart() * complexNumber.getImagePart());
            return new Complex(newRealPart, newImagePart);
        }
        //重写toString方法
        public String toString(){
            if(this.imagePart>0){
                return this.realPart+"+"+this.imagePart+"i"; //如果是虚部是正数，需要手动添加 +
            }else if(this.imagePart<0){
                return this.realPart+this.imagePart+"i";//如果虚部是负数，不用给你手动添加 -（运算的结果自带）
            }else return this.realPart+" ";
        }
    }

---

2、测试复数类

import java.util.Scanner;

//测试封装的复数类，实现负数的四则运算
public class ComplexTest {
    //这里我们可以采取从键盘中输入复数的实部和虚部
    public static void main(String[] args) {
        double realPart ;
        double imagePart ;
        Scanner s = new Scanner(System.in);
        System.out.print("输入第一个复数的实部：");
        realPart = s.nextDouble();
        System.out.print("输入第一个复数的虚部：");
        imagePart = s.nextDouble();
        Complex complex1 = new Complex(realPart,imagePart);
        System.out.print("输入第二个复数的实部：");
        realPart = s.nextDouble();
        System.out.print("输入第二个复数的虚部：");
        imagePart = s.nextDouble();
        Complex complex2 = new Complex(realPart,imagePart);
        //测试复数的加减乘除
        System.out.println("加法："+ complex1.add(complex2));
        System.out.println("减法："+complex1.sub(complex2));
        System.out.println("乘法："+complex1.mul(complex2));
        System.out.println("除法："+complex1.division(complex2));
    }
}

---

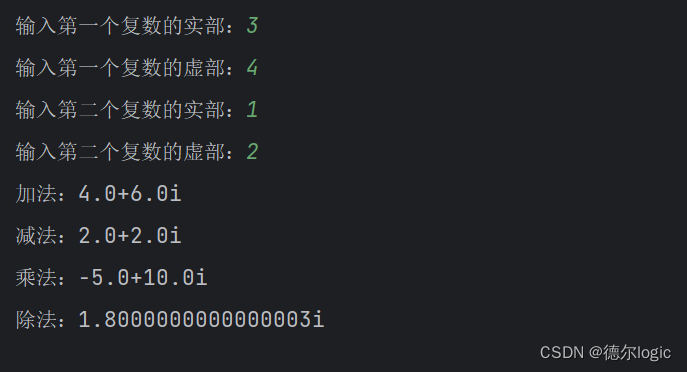
3、代码测试结果