题目描述:

有一天，小明发现他的影子长度随着他在灯泡和墙壁之间走动时会发生变化，一个突发奇想在他的脑海里闪过，他现在想知道他来回走动，他的影子的最大长度是多少？

输入格式:

第一行包含一个整数T (T <= 100),表示测试数据的级数。

对于每组测试数据仅一行包含三个实数 H, h 和 D。 H 是灯光的高度， h小明的身高，D是灯光和墙壁的水平距离。三个数的范围都在 10-2 到 103之间 ,   H - h >= 10-2。

输出格式:

共T行，每组测试数据占一行，表示影子的长度，保留三位小数。

样例输入:

3
2 1 0.5
2 0.5 3
4 3 4

样例输出:

1.000
0.750
4.000

提示:

三分的模板：

double l = 0, r = 1e9;
while (r-l >= 1e-3) {
	double m1 = l+(r-l)/3,  m2 = r-(r-l)/3;
	if (  f(m1) < f(m2) )  l = m1;
	else r = m2;
}

时间限制: 1000ms
空间限制: 256MB

题解：

求人从左向右走动时，影子的长度L的最大值

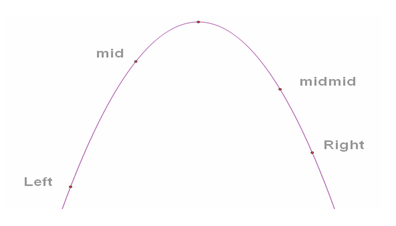
人在灯下的影子长度是0，这时他如果向前走的话，影子会逐渐变长，到最后人走到墙的位置的时候，影长度便是人的身高了，所以影长的变化曲线要么是单调递增的,并且是向上凸的，所以适合三分。（二分法作为分治中最常见的方法，适用于单调函数，逼近求解某点的值，当函数是凸性函数时，就得用三分）。

由于影长从灯下0一直到恰好没投影到墙上的过程是一个单调的过程，我们可以直接求更新答案。用三分算法求解投影到墙上后影长的变化即可。

 

代码如下：

#include<cstdio>
double H,h,D;
double f(double m){
	double a=(H-h)/(m-D),b=H+a*D;
	if(b>=0) return b+m;
	else return -b/a+m;
}
int main(){
	int T;
	scanf("%d",&T);
	while(T--){
		scanf("%lf %lf %lf",&H,&h,&D);
		double l=0,r=D;
		while(r-l>1e-5){
			double m1=l+(r-l)/3,m2=r-(r-l)/3;
			if(f(m1)<f(m2)) l=m1;
			else r=m2;
		}
		printf("%.3lf\n",f(l));
	}
}