$Part$ $1$ 读题

题目描述

$wgy$有$n$个很不错的数，第$i$个数是$a_i$，他想用它们组一棵数树送给$ayb$。

$ayb$对一棵数树的喜爱程度是这棵数树的每个子树包含的数的和的总和。简单来说，$ayb$对一棵数树的喜爱程度是这样计算的：$su{m}_1+su{m}_2+su{m}_3+\dots +su{m}_n$，其中$su{m}_u$表示以$u$为根的子树的数和。

为了令$ayb$最开心，$wgy$想组出一棵他喜爱程度最高的数树。但是$wgy$太笨了，你能帮助$wgy$吗？

输入格式

第一行一个整数$n$。

接下来一行$n$个整数，表示$wgy$手里的数$a_i$。

输出格式

一行，一个整数表示最高的喜爱程度。

输入样例

2
1 2

输出样例

5

数据范围与提示

对于$20\%$的数据，$n\le 100$

对于$100\%$的数据，$1\le n\le 10^5$，$1\le a_i\le 10^7$

$Part$ $2$ 思路

本题看似很难，甚至可能都理解不了题意（例如题目中的“$su{m}_u$表示以$u$为根的子树的数和”）。但是仔细想想，实际上就变得简单了许多。我们分析一下。

我们思考一下，在什么状态下，喜爱程度能达到最高。可能文字大家不能理解，我这里用几幅图来表示。

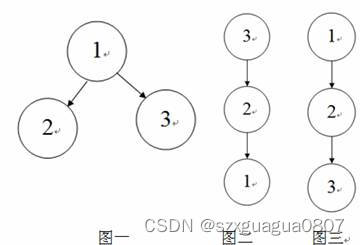
可以发现，图一的喜爱程度为$1+2+3=6$，图二的喜爱程度为$(1+2+3)+(2+3)+3=14$，图三的喜爱程度为$(3+2+1)+(2+1)+1=10$。很明显，图二的喜爱程度是最高的。同时，我们也可以推出喜爱程度的计算方法：$s+=a[i]\times a[i]$（这里也可以写$i$，此处$s$代表喜爱程度总和）

由此，我们可以得出一个规律：在竖状且从小到大排序的情况下，喜爱程度是最高的。在输入后，我们需要先进行排序（冒泡排序、选择排序、$sort$快速排序都可以），然后算出喜爱程度就可以了。也就是如下代码：

sort(a+1,a+1+n);//此处采用sort快排
for(int i=1;i<=n;i++)s+=i*a[i];//此处i、a[i]都可以用

然后我们再加上定义、输入和输出就可以啦！

小tip：大家可以先根据思路，写一下代码哦！

$Part$ $3$ 代码

注意！！！我这里提供$sort$快速排序，其他排序方法大家自行修改$sort$部分

#include<bits/stdc++.h>
using namespace std;
unsigned long long n,a[100005],s;
int main(){
	cin>>n;
	for(int i=1;i<=n;i++)cin>>a[i];
	sort(a+1,a+1+n);//此处采用sort快排
	for(int i=1;i<=n;i++)s+=i*a[i];//此处i、a[i]都可以用
	cout<<s;
	return 0;
}

听完后，是不是觉得很简单呢？赶快自己去试一下吧！！！