一、说明
计量经济学是使用统计方法来发展理论或测试经济学或金融学中的现有假设。计量经济学依赖于回归模型和零假设检验等技术。计量经济学也可以用来预测未来的经济或金融趋势。

图片来源:https://marketbusinessnews.com
二、 计量经济之简介
计量经济学是对经济学、精算学和金融学中关系的衡量标准。应用计量经济学时,需要遵循一系列步骤,其中包括:陈述假设、收集数据、估计关系和评估模型。
计量经济学可以使用各种各样的数据,包括:时间序列数据、横截面数据和合并数据。为了进行精算研究,必须了解计量经济学的方法,并能够区分所呈现的数据类型。
2.1 计量经济学
计量经济学衡量变量之间的关系。评估变量之间的关系涉及八个步骤。这些步骤包括:
- 陈述假设。
- 收集数据。
- 指定理论的数学表示。
- 指定理论的计量经济学模型。
- 估计参数。
- 测试模型的规范。
- 检验假设。
- 使用模型进行预测。
2.2 数据类型
可以收集的三种类型的数据包括:时间序列数据、横截面数据和合并数据。
- 时序数据收集一段时间内的数据。
- 横断面数据使用同一时间段从不同区域收集数据。
- 合并数据结合了时间序列和横截面原则。
2.3 指定、解释和验证模型
指定、解释和验证模型对于测试您陈述的假设非常重要。结果仅与使用的模型和数据一样好。
三、进行精算研究----概率和概率分布

罗伊·波兰尼策
·
跟随
5 分钟阅读
·
13月 <>
概率分布是理想化的频率分布。频率分布描述特定的样本或数据集。它是变量的每个可能值在数据集中出现的次数。某个值在样本中出现的次数由其出现概率决定。

3.1. 概率知识简介
本主题演示如何构造概率分布。我们将研究无条件和条件概率,并讨论如何处理具有相关和独立事件的联合概率。
当我们讨论贝叶斯定理和条件函数时,引入了一些复杂性。为了进行精算研究,必须熟悉概率术语和所讨论的不同类型的概率分布。
3.2. 随机变量
随机变量是由偶然决定的不确定结果。概率分布列出了实验的所有可能结果及其关联的概率。
离散随机变量具有与特定单数结果相关的正概率。连续随机变量具有与一系列结果值相关的正概率 - 它等于任何单个值的概率为零。
3.3. 事件的概率
概率的两个属性是:
- 所有可能的互斥事件的概率之和为 1。
- 任何事件的概率都不大于 1 或小于 0。
无条件概率(边际概率)是事件发生的概率;条件概率, P(A|B),是给定另一个事件(B)发生时事件(A)发生的概率。乘法的一般规则用于求一个事件以另一个事件为条件时发生两个事件的概率为 P(A 和 B) = P(A|B) × P(B)。
加法的一般规则是 P(A 或 B) = P(A) + P(B) - P(AB)。一个独立事件的概率不受其他事件的发生的影响,但一个从属事件的概率会随着另一个事件的发生而改变。
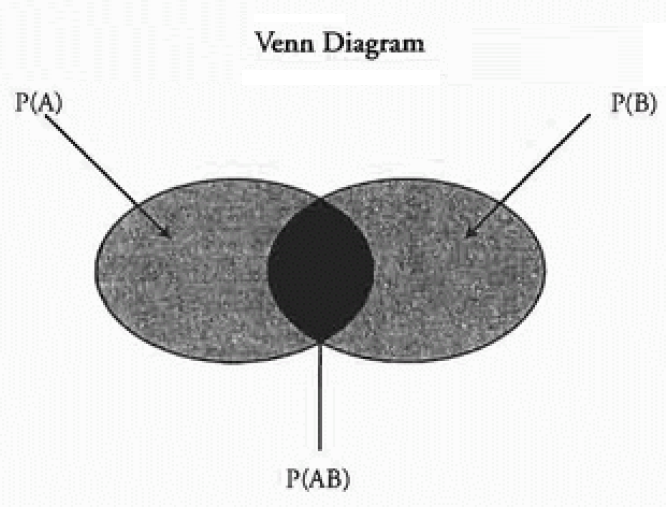
一组独立事件中的任何一个发生的概率是它们的概率之和,它们都发生的概率是它们的概率的乘积。
3.4. 相对频率
相对频率是落在每个区间内的总观测值的百分比。
3.5. 贝叶斯公式
基于事件 O 的发生更新概率的贝叶斯公式为:P(I|O) = P(I) × P(O|I) / P(O)
3.6. 概率函数
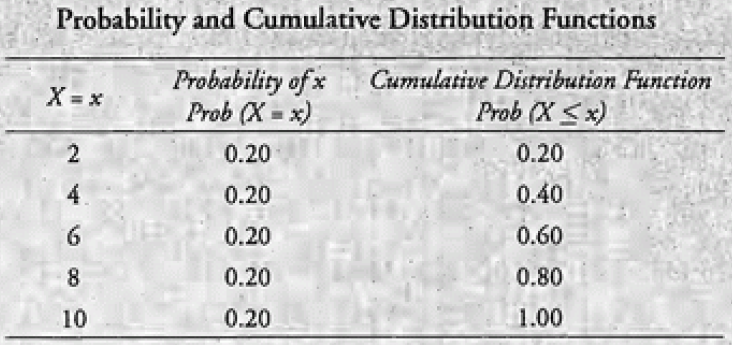
概率函数指定随机变量等于特定值的概率;P(X = x) = p(x)。概率密度函数 (pdf) 是连续随机变量的概率函数表达式。
累积分布函数 (cdf) 给出随机变量等于或小于每个特定值的概率。它是指定值左侧概率分布下的区域。
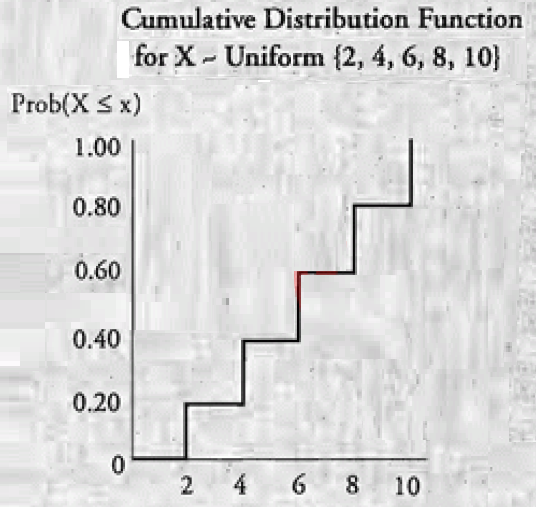
3.7. 离散均匀分布
离散均匀分布是存在 » 离散的、可能性相等的结果,因此对于每个结果 p(x) = 1/n。
3.8. 正态分布
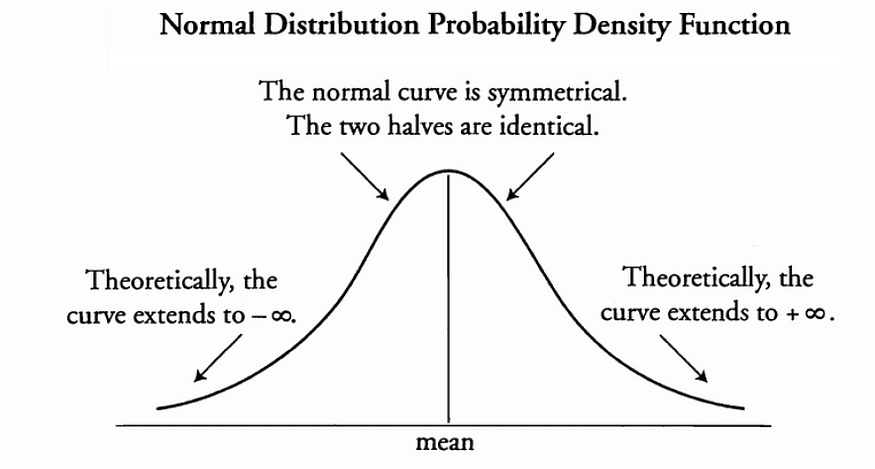
正态概率分布和正态曲线具有以下特征:
- 正态曲线是对称的,呈钟形,单个峰值位于分布的正中心。
- 正态分布可以完全由其均值和标准差定义。
3.9. 单变量和多变量分布
多元分布描述随机变量组。
3.10. 联合分配
联合概率分布是指两个或多个事件的发生。如果 X 和 Y 是离散随机变量,则条件概率函数表示为:
P(Y = y |X = x) = f(x,y) / f1(x)
四、第 3 部分:概率分布的特征
概率分布描述了给定数据生成过程的可能值的预期结果。概率分布有多种形状,具有不同的特征,由平均值、标准差、偏度和峰度定义。

图片来源:https://slideplayer.com
4.1. 简介
本主题讨论期望值、方差、标准差、协方差、相关性、偏度和峰度的概念。我们将评估这些措施的特征,并从总体和样本的角度检查其计算结果。
其他涉及的概念包括切比雪夫不等式和变异系数。为了进行精算研究,必须了解方差和标准差之间的关系以及协方差和相关性之间的关系。
4.2. 期望值
随机变量 X 具有可能值 x1,...,xn 的期望定义为:
![]()
4.3. 方差
随机变量的方差定义为:
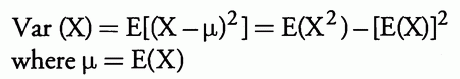
方差的平方根称为标准差。方差或标准差提供平均值周围随机变量值离散程度的度量。
如果 X 和 Y 是自随机变量,则:
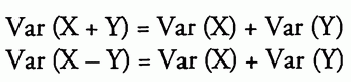
4.4.切比雪夫不等式
切比雪夫不等式指出,对于所有 k > 1,均值 k 个标准差内的观测值比例至少为 1–1/k²。
4.5. 变异系数
变异系数,
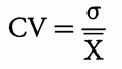
表示相对于分布均值的离散(风险)。
4.6. 投资组合预期和方差
2资产投资组合的预期回报和方差由下式给出:

4.7. 有条件和无条件的期望和方差
条件预期用于投资,以便在条件反射事件发生时更新预期。
4.8. 人口与样本
总体包括指定组的所有成员,而样本是用于推断总体的总体子集。
算术平均值为:
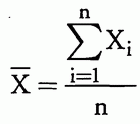
几何平均值为:
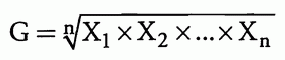
中位数是数据集从大到小排列时的中点,数据集的众数是出现频率最高的值。方差定义为与算术平均值的平方偏差的平均值。
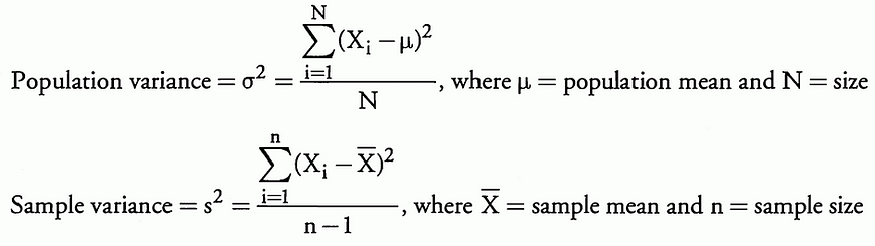
相关性是两个随机变量之间关联的标准化度量;它的值范围从 — 1 到 +1,等于
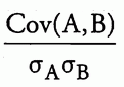
4.9. 偏度和峰度
偏度描述了分布与其均值不对称的程度。右偏分布具有正样本偏度,并且均值高于高于中位数,高于众数。
左偏分布具有负偏度,并且均值低于中位数,低于众数。
峰度测量分布的峰值和极端结果的概率。相对于正态分布测量过量峰度,正态分布的峰度为 3。
过量峰度的正值表明其分布是软骨(肥尾,更尖)。过量峰度的负值表示扁平分布(钢轨较细,峰值较少)。
绝对值大于 1 的过量峰度被认为是大的。
五、一些重要的概率分布
5.1 简介
本主题详细说明了如何评估具有正态分布的概率。我们将看到如何使用标准正态概率表(z-table)以及如何从总体数据集中抽取样本。
还讨论了 t 分布、卡分布和 F 分布的特征。本文讨论了正态分布的性质以及如何进行简单的随机抽样。
5.2. 正态分布
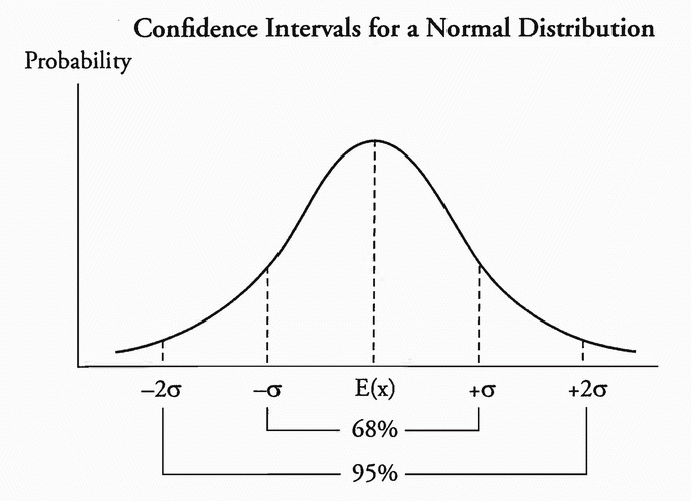
标准正态分布(z 分布)用于在总体方差已知时为总体均值构建置信区间。
5.3. 从正态分布中抽样
简单随机抽样是一种选择样本的方法,其方式是被研究人群中的每个项目或人员具有相同的可能性被纳入样本。抽样误差是样本统计量与其相应的总体参数(例如,样本均值减去总体均值)之间的差值。
抽样分布是从同一总体中随机抽取的相同大小的样本计算样本统计量时可以采用的所有值的分布。
5.4. 中心极限定理
中心极限定理指出,对于具有平均μ和有限方差 σ² 的总体,大小为 n 的所有可能样本的样本均值的抽样分布将近似正态分布,均值等于 μ,方差等于 σ²/n。
样本均值的标准误是样本均值分布的标准差,计算公式为:
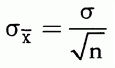
其中σ,总体标准差,是已知的。
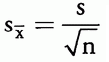
其中 s 是样本标准差,总体标准差未知。
5.5. T 分布
t 分布与形状上的正态分布相似但不完全相同 — 它由自由度定义,具有较低的峰值,并且具有更粗的尾巴。分布的自由度等于 n — 1;当 DF 较大时,t 分布更接近正态分布,当 df 较大时,置信区间较窄。
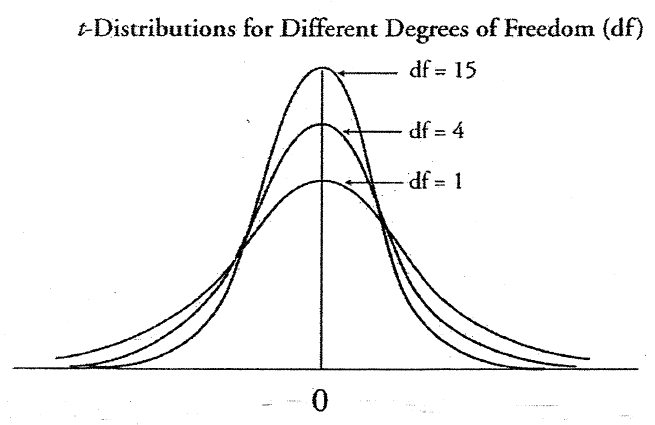
当总体方差未知时,t 分布用于构造总体均值的置信区间。
t 分布是假设检验中使用最广泛的分布。当样本数量较小时,此分布用于估计正态分布总体的均值,并用于检验两个样本均值或小样本量的置信区间之间差值的统计显著性。
自由度≥ 1 且必须是整数。
5.6. 气分布
单个总体方差检验使用卡方检验。卡方是主要用于假设检验的分布,它与伽马分布和标准正态分布有关。
例如,独立正态分布的和分布为具有 k 个自由度的卡方 (χ²)。自由度> 1,并且必须是 300 <整数。

5.7. F 分布
比较两个方差的检验使用 F 分布检验统计量。F 分布,也称为费雪-斯奈德科分布,也是另一个最常用于假设检验的连续分布。

具体而言,它用于检验方差检验和似然比检验分析中两个方差之间的统计差异。分子自由度 (N) > 1 和分母自由度 (M) > 1,两者都必须是整数。
六 后记
本文回顾了概率和统计学知识,为以后进行精算做了理论铺垫,在本系列中,我们将展开一系列精算理念和研究,这是一个开端。
参考文章:
Conducting Actuarial Studies — Part 4: Some Important Probability Distributions | by Roi Polanitzer | Medium