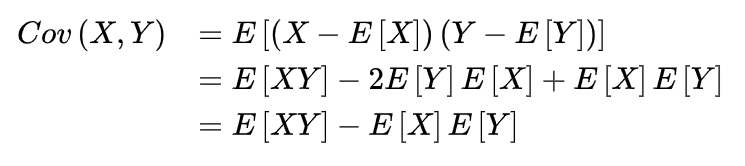大家好,我是 方圆。关于各类区间和问题有很多种解法,我们可以根据题目要求选择解题的方向:
-
数组不变,区间查询:前缀和、树状数组和线段树
-
数组单点查询,区间查询:树状数组 和线段树
-
数组区间修改,单点查询:差分 和线段树
-
数组区间修改,区间查询:线段树
树状数组是其中能解决问题最多的,而且它相比于线段树代码量更少更简单,是我们 优先选择的方法。在本文我们对线段树进行介绍,并在文末附上相关的习题供大家练习。如果大家想要找刷题路线的话,可以参考 Github: LeetCode。
树状数组
树状数组(BIT, Binary Indexed Tree)是简洁优美的数据结构,它能在很少的代码量下支持 单点修改 和 区间查询,我们先以 a[] {1, 2, 3, 4, 5, 6} 数组为例建立树状数组看一下树状数组的样子:
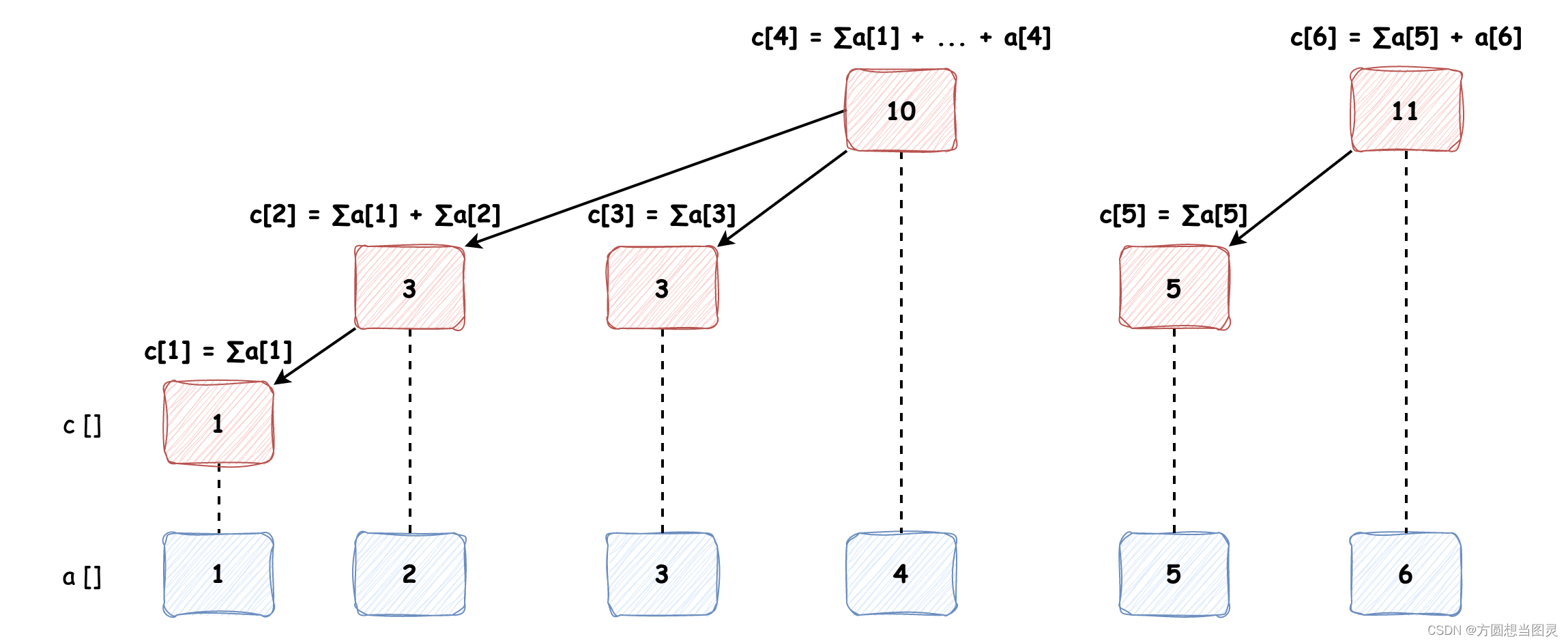
可以发现:不是所有节点都是连接在一起的,c[1], c[2], c[3], c[4] 和 c[5], c[6] 分别构成了两棵树;奇数索引位置的节点只管辖一个数组元素(我们例子中以 1 为起始索引)。那么这个树状数组是怎么计算和推导出来的呢?
管辖的区间
树状数组的每个元素会管辖多少个数组元素?也就是说每个元素的区间长度是多少?我们从上图中已经知道了奇数的树状数组元素只管辖一个元素,区间为 c[x] = [x, x],那么我们只需再研究下偶数元素管辖的区间长度即可。
- c[y] 所管辖的区间长度为 2k ,其中 k 为 y 的 2 进制表示中最低位 1 后面所有 0 的数量;c[y] 所管辖的区间为:[y - 2k + 1, y]
我们以 c[4] 为例,它管辖多少个元素呢?4 的 2 进制表示为 0100,最低位 1 后面 0 的数量为 2,即 k = 2,那么 2k = 22 = 4,所以它管辖的区间长度为 4,也就是 4 个数组元素,区间为 [4 - 4 + 1, 4] = [1, 4]。
父节点是谁?
现在我们知道每个元素所管辖的区间范围了,那么我们怎么才能知道它的父节点是谁呢?就比如说我们现在得到了 c[1] 元素,我们想知道它的父节点,要怎么计算呢?
- c[x] 的父节点为 c[x + lowbit(x)]
怎么回事?其中的 lowbit(x) 是什么东西?其实它的值和 2k 一致,其中 k 为 x 的 2 进制表示中最低位 1 后面所有 0 的数量,熟悉不熟悉?这个 lowbit(x) 和我们上文中计算该元素所管辖区间长度的值一致!这不就简单了!
-
lowbit(x) 的计算方法:lowbit(x) = x & -x
我们以计算 c[2] 为例,lowbit(2) = 2 & -2,其中 2 的 2 进制表示为 0010,-2 的 2 进行表示为 1110,它的计算方法为将 2 的所有非符号位二进制全部取反后再加 1,即 1101 + 1 = 1110,执行 & 运算后结果为 0010,十进制表示为 2,与 21 值一致。lowbit 的计算用代码表示为:
int lowbit(int x) { return x & -x; }
我们以 c[1] 节点为例计算下它的父节点是谁,lowbit(1) = 1 & -1 = 0001 & 1111 = 0001 = 1,那么它的父节点为 c[1 + 1] = c[2],与图上表示的一致。
现在我们已经知道如何通过计算来创建树状数组了, 接下来我们要看下它的应用。
区间查询
区间查询我们先讨论计算前 N 项和的方法,比如我们现在要查询前 6 项和,我们来看下它查询的过程:
- 从 c[6] 开始找子节点,有 c[6] 管辖的区间为 [5, 6],那么再往下找需要找 c[4],它的区间为 [1, 4],计算这两个节点的和即可。
那么从 c[6] 跳到 c[4] 是如何计算出来的呢?我们可以通过 c[6] 区间的下界减 1 来得到,转换成公式表示即为 x - lowbit(x) = 6 - 2 = 4,当它跳到 c[4] 时发现已经满足求和条件,不再向下跳而结束查找,而且我们可以通过计算 4 - lowbit(4) = 4 - 4 = 0 ,可以发现当 x - lowbit(x) = 0 时为结束查找的条件。我们用代码来表示为:
int query(int x) {
int res = 0;
for (int i = x; i > 0; i -= lowbit(i)) {
res += c[i];
}
return res;
}
那么我们计算区间 [3, 6] 的和该如何计算呢?我们从图中可以发现,先计算出[1, 6] 和 [1, 2] 的和,再使用前者减去后者即为所得,用代码表示为:
int query(int left, int right) {
return query(right) - query(left - 1);
}
单点修改
如果我们要修改 a[x] 的值,我们仅需要修改所有管辖了 a[x] 的 c[y] 即可,而 a[x] 可能会被多个 c[y] 管辖,这些所有的 c[y] 节点该如何确定呢?我们可以回头再去看看前面的树状数组配图,比如我们要修改 a[1] 的值,那么我们需要修改 c[1], c[2] 和 c[4] ,能不能发现它是在不断的 跳父节点 修改?所以,如果我们要修改数组中某个元素的值,树状数组的更新则是不断地更新父节点值。好,我们直接上代码吧:
// 将 index 索引处的值更新为 num
void update(int index, int num) {
a[index] = num;
add(index, num - a[index]);
}
// 更新 c[index] 的值,变化差值为 val
void add(int index, int val) {
for (int i = index; i <= c.length; i += lowbit(i)) {
c[i] += val;
}
}
建树
好了,区间查询和单点修改我们都讲完了,但是从头到尾我们还没说过树状数组是怎么建立的呢。我们可以想一下,c 数组初始化时每个索引处的值都为 0,建树仅需要将 a 数组中所有值都在树状数组中执行单点修改即可:
public BinaryIndexedTree(int[] a) {
this.a = a;
this.c = new int[a.length + 1];
for (int i = 0; i < a.length; i++) {
add(i + 1, a[i]);
}
}
到这里我们基本上已经将树状数组讲解完毕了,它的全量代码如下:
public class BinaryIndexedTree {
int[] a;
int[] c;
public BinaryIndexedTree(int[] a) {
this.a = a;
this.c = new int[a.length + 1];
for (int i = 0; i < a.length; i++) {
add(i + 1, a[i]);
}
}
// 将 index 索引处的值更新为 num
void update(int index, int num) {
a[index] = num;
add(index, num - a[index]);
}
// 更新 c[index] 的值,变化差值为 val
void add(int index, int val) {
for (int i = index; i < c.length; i += lowbit(i)) {
c[i] += val;
}
}
int query(int left, int right) {
return query(right) - query(left - 1);
}
// 查询前缀和的方法
int query(int x) {
int res = 0;
for (int i = x; i > 0; i -= lowbit(i)) {
res += c[i];
}
return res;
}
int lowbit(int x) {
return x & -x;
}
}
我们需要掌握或背过这个模板,并不断的做题练习。
相关题目
- 307. 区域和检索 - 数组可修改
本题是最典型的树状数组的应用,涉及单点修改和区间查询,使用线段树修改对应索引位置的数即可。
- 1310. 子数组异或查询
本题是求区间和线段树的变体,它求的是区间异或结果,异或运算的特点是二进制位相同的异或计算结果为 0,不同的异或计算结果为 1,我们可以根据这个特点计算进行区间异或计算,比如说我们要查询区间 [3, 5] 的异或结果,那么可以使用 [1, 5] 区间结果异或 [1, 2] 区间结果,相当于在区间 [1, 5] 中去掉了 [1, 2]。
- 775. 全局倒置与局部倒置
本题是对上述使用线段树的变体,前两道题中的线段树记录的是所有数组中的元素值,而本题的线段树记录的是数组中各个元素出现的次数,而且题目要求所有数字不同,这体现在线段树中就是出现过的数字被标记为 1,未出现过的数字被标记为 0。全局倒置和局部倒置相当于是计算逆序对的数量,全局倒置是在线段树中查询区间 (x, n] 中出现数字的数量(x 为当前数),局部倒置更加简单,判断当前数是否比前一个数小即可。
- 1395. 统计作战单位数
本题和上一题类似,也是标记数值出现的次数,但是解法可能没办法一下就想到。我们每次标记士兵 i 和士兵 k,当 rating[i] < rating[k] 时统计区间 (i, k) 内士兵 j 的数量,当 rating[i] > rating[k] 时查询区间 (k, i) 内士兵 j 的数量,并且每次统计完成后需要将线段树标记清零,避免造成不符合题意的统计结果,时间复杂度为 O(n2logm)。
- 327. 区间和的个数
说实话,这道题我第一次看答案都没写出来。现在我们从头捋一下,一步步地把题解写出来。根据题目中提到子数组 区间和,且不涉及区间的修改,我们能够想到使用前缀和的方法来求解,根据 前缀和作差能够计算出任意区间和 的特点,我们再进一步考虑如何实现。
我们记前 i 项的前缀和为 s,s = sum[0, i],其中 0 <= i <= nums.length - 1,其中必然存在某区间满足题意要求,我们记 s = sum[0, k] + sum[k + 1, i],其中 k < i,若 sum[k + 1, i] 符合题意要求,则有:
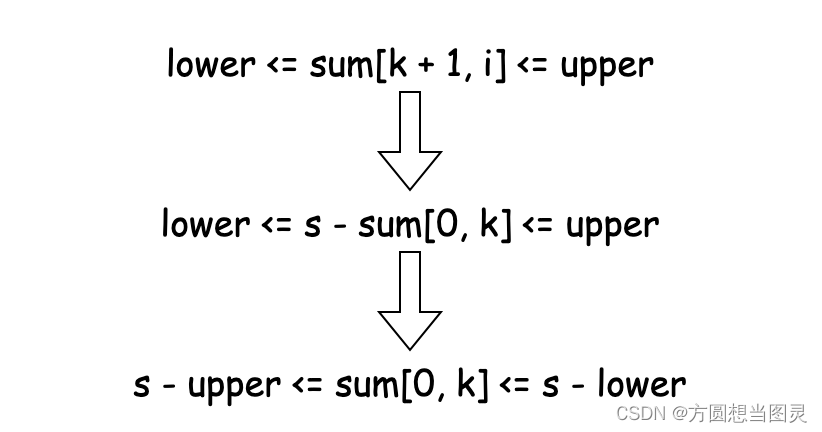
那么我们可以根据以上结果得出,任意区间 [0, i] 内符合题意的数量等于该区间内前缀和满足 [s - upper, s - lower] 条件的数量(i 为我们当前处理的索引位置,s 为当前 i 项前缀和,k 为已经处理过的索引位置),这样我们能够使用树状数组标记前缀和的值(sum[0, k]),并计算区间内值的数量得出结果。但是由于数组中每个数范围很大,会导致值域爆炸,所以需要采用离散化的方法,这样才能在树状数组中对值进行标记。
离散化是指当我们只关心数据的大小关系时,用排名代替原数据进行处理的一种预处理方法。离散化本质上是一种哈希,它在保持原序列大小关系的前提下把其映射成正整数。当原数据很大或含有负数、小数时,难以表示为数组下标,导致一些算法和数据结构(如BIT)无法运作,这时我们就可以考虑将其离散化。
好了,基本思路已经确定了,我们看下具体代码实现,关注其中的注释即可:
public int countRangeSum(int[] nums, int lower, int upper) {
// 使用 set 记录下所有的前缀和前缀和需要满足的题意范围的值,供我们做离散化使用
// 之所以使用 set 是因为我们只需要知道它在树状数组中的位置,而不要求它的数量
Set<Long> set = new HashSet<>();
long preSum = 0L;
// 需要将前缀和 0 也标记进来,它是原数组索引 0 处值的前缀和
set.add(preSum);
for (int j : nums) {
preSum += j;
set.add(preSum);
set.add(preSum - upper);
set.add(preSum - lower);
}
// 所有的值都有了,我们进行离散化处理
ArrayList<Long> list = new ArrayList<>(set);
Collections.sort(list);
// 使用 hashmap 来保存值对应在树状数组的索引
HashMap<Long, Integer> map = new HashMap<>();
for (int i = 0; i < list.size(); i++) {
map.put(list.get(i), i + 1);
}
int res = 0;
BinaryIndexedTree tree = new BinaryIndexedTree();
// 前缀和从 0 开始计算
preSum = 0L;
// 标记数组索引 0 前的前缀和在树状数组中的位置
tree.update(map.get(0L));
for (int num : nums) {
preSum += num;
int left = map.get(preSum - upper);
int right = map.get(preSum - lower);
res += tree.query(left, right);
// 更新该前缀和在树状数组中的位置
tree.update(map.get(preSum));
}
return res;
}
static class BinaryIndexedTree {
int[] tree;
public BinaryIndexedTree() {
// 数组长度为 1e5 我们需要把对应的范围值也保存上,所以需要 * 3
tree = new int[(int) 3e5 + 1];
}
public void update(int index) {
for (int i = index; i < tree.length; i += lowbit(i)) {
tree[i] += 1;
}
}
public int query(int left, int right) {
return query(right) - query(left - 1);
}
public int query(int index) {
int res = 0;
for (int i = index; i > 0; i -= lowbit(i)) {
res += tree[i];
}
return res;
}
private int lowbit(int i) {
return i & -i;
}
}
巨人的肩膀
-
树状数组(简单介绍)
-
负数的二进制表示方法(正数:原码、负数:补码)
-
树状数组
-
算法学习笔记(2) : 树状数组
-
维基百科 - 树状数组
-
关于各类「区间和」问题如何选择解决方案(含模板)
-
算法学习笔记(19): 离散化






![WinRAR<6.23 远程代码执行漏洞【Poc公开】(CVE-2023-38831) [有POC]](https://img-blog.csdnimg.cn/4528e8cc518543979bf02f59e69eb207.png)