快速幂

一.暴力解法 O(n∗b) 会TLE

#include<iostream>
using namespace std;
int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        int a,b,p;
        long long res=1;
        cin>>a>>b>>p;
        while(b--)
            res = res * a %p;
        cout<<res<<endl;
    }
}

二.快速幂解法 O(n∗logb)

我们练习一下：

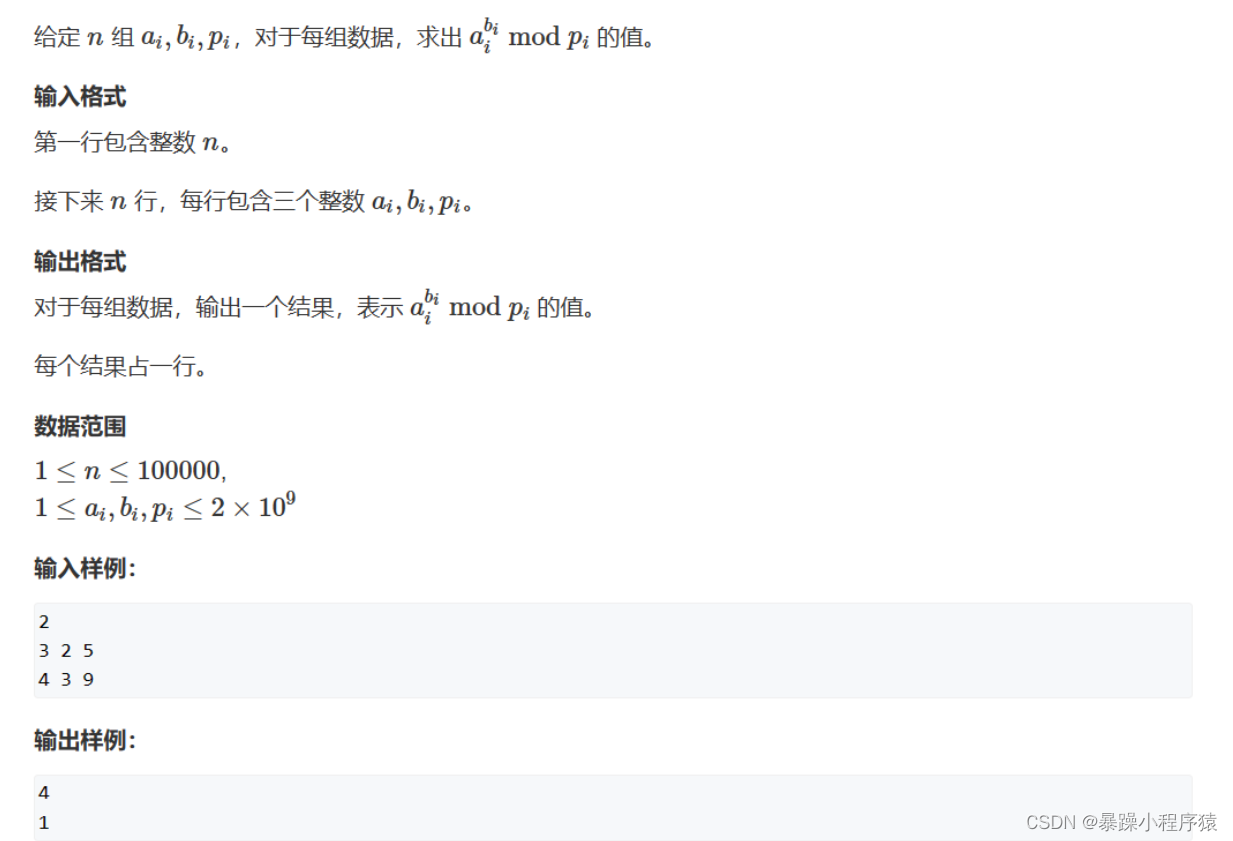
2.1快速幂之迭代版 O(n∗logb)

#include<iostream>
using namespace std;
long long qmi(long long a,int b,int p)
{
    long long res=1;
    while(b)//对b进行二进制化,从低位到高位
    {
        //如果b的二进制表示的第0位为1,则乘上当前的a
        if(b&1) res = res *a %p;
        //b右移一位
        b>>=1;
        //更新a,a依次为a^{2^0},a^{2^1},a^{2^2},....,a^{2^logb}
        a=a*a%p;
    }
    return res;
}
int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        cin.tie(0);
        ios::sync_with_stdio(false);
        int a,b,p;
        long long res=1;
        cin>>a>>b>>p;
        res = qmi(a,b,p);
        cout<<res<<endl;
    }
    return 0;
}

2.2快速幂之递归版 O(n∗logb)

#include<iostream>
using namespace std;
#define ull unsigned long long
ull quick_pow(ull a,ull b,ull p)
{
    if(b==0) return 1;
    a%=p;
    ull res=quick_pow(a,b>>1,p);
    if(b&1) return res*res%p*a%p;
    return res*res%p;
}
int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        int a,b,p;
        cin.tie(0);
        ios::sync_with_stdio(false);
        cin>>a>>b>>p;
        cout<<quick_pow(a,b,p)<<endl;
    }
    return 0;
}

三：快速幂练习(快速幂求逆元)

#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;
LL qmi(int a,int b,int p)
{
    LL res=1;
    while(b)
    {
        if(b&1) res=res*a%p;
        a=a*(LL)a%p;
        b>>=1;
    }
    return res;
}
int main()
{
    int n;
    scanf("%d",&n);
    while(n--)
    {
        int a,p;
        scanf("%d%d",&a,&p);
        if(a%p) printf("%lld\n",qmi(a,p-2,p));
        else puts("impossible");
    }
    return 0;
}