比赛链接

https://leetcode.cn/contest/biweekly-contest-111

Q1：6954. 统计和小于目标的下标对数目

https://leetcode.cn/problems/count-pairs-whose-sum-is-less-than-target/

提示：
1 <= nums.length == n <= 50
-50 <= nums[i], target <= 50

解法1——$O(n^2)$暴力

class Solution {
    public int countPairs(List<Integer> nums, int target) {
        int ans = 0, n = nums.size();
        for (int i = 0; i < n; ++i) {
            for (int j = i + 1; j < n; ++j) {
                if (nums.get(i) + nums.get(j) < target) ans++;
            }
        }
        return ans;
    }
}

解法2——排序+双指针 $O(n\log n)$

排序之后使用双向双指针，

class Solution {
    public int countPairs(List<Integer> nums, int target) {
        Collections.sort(nums);
        int ans = 0, l = 0, r = nums.size() - 1;
        while (l < r) {
            if (nums.get(l) + nums.get(r) < target) {
                ans += r - l;
                l++;
            } else r--;
        }
        return ans;
    }
}

Q2：8014. 循环增长使字符串子序列等于另一个字符串

https://leetcode.cn/problems/make-string-a-subsequence-using-cyclic-increments/

提示：
1 <= str1.length <= 10^5
1 <= str2.length <= 10^5
str1 和 str2 只包含小写英文字母。

双指针

其实就是双指针判断子序列那道题目，除了可以相同匹配外，还可以循环+1后匹配。

class Solution {
    public boolean canMakeSubsequence(String s1, String s2) {
        int m = s1.length(), n = s2.length();
        int i = 0, j = 0;
        while (i < m && j < n) {
            // 如果可以匹配上
            if (s1.charAt(i) == s2.charAt(j) || (s1.charAt(i) + 1 - 'a') % 26 == (s2.charAt(j) - 'a') % 26) ++j;
            ++i;
        }
        return j == n;
    }
}

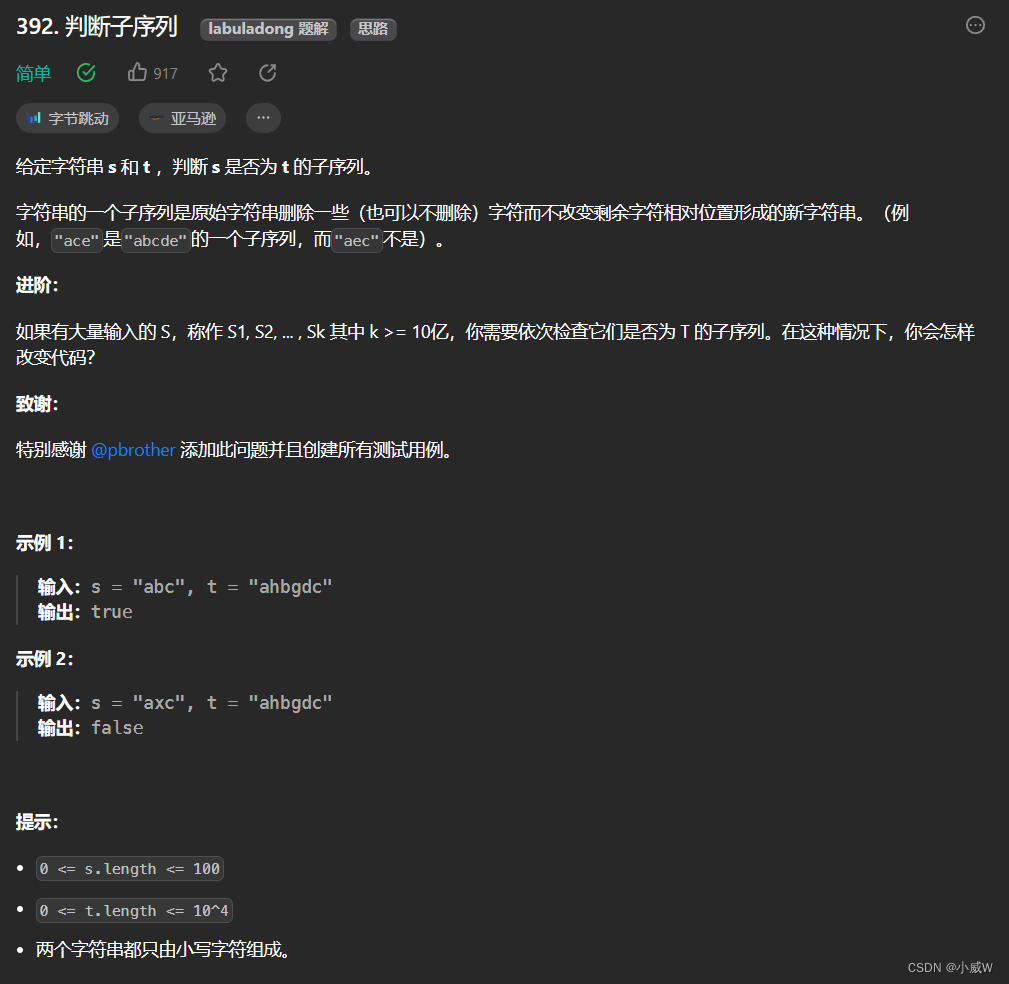
相似题目——392. 判断子序列

https://leetcode.cn/problems/is-subsequence/description/

class Solution {
    public boolean isSubsequence(String s, String t) {
        int n1 = s.length(), n2 = t.length();
        int i = 0, j = 0;
        while (i < n1 && j < n2) {
            if (s.charAt(i) == t.charAt(j)) i++;
            j++;
        }
        return i == n1;
    }
}

Q3：6941. 将三个组排序

https://leetcode.cn/problems/sorting-three-groups/

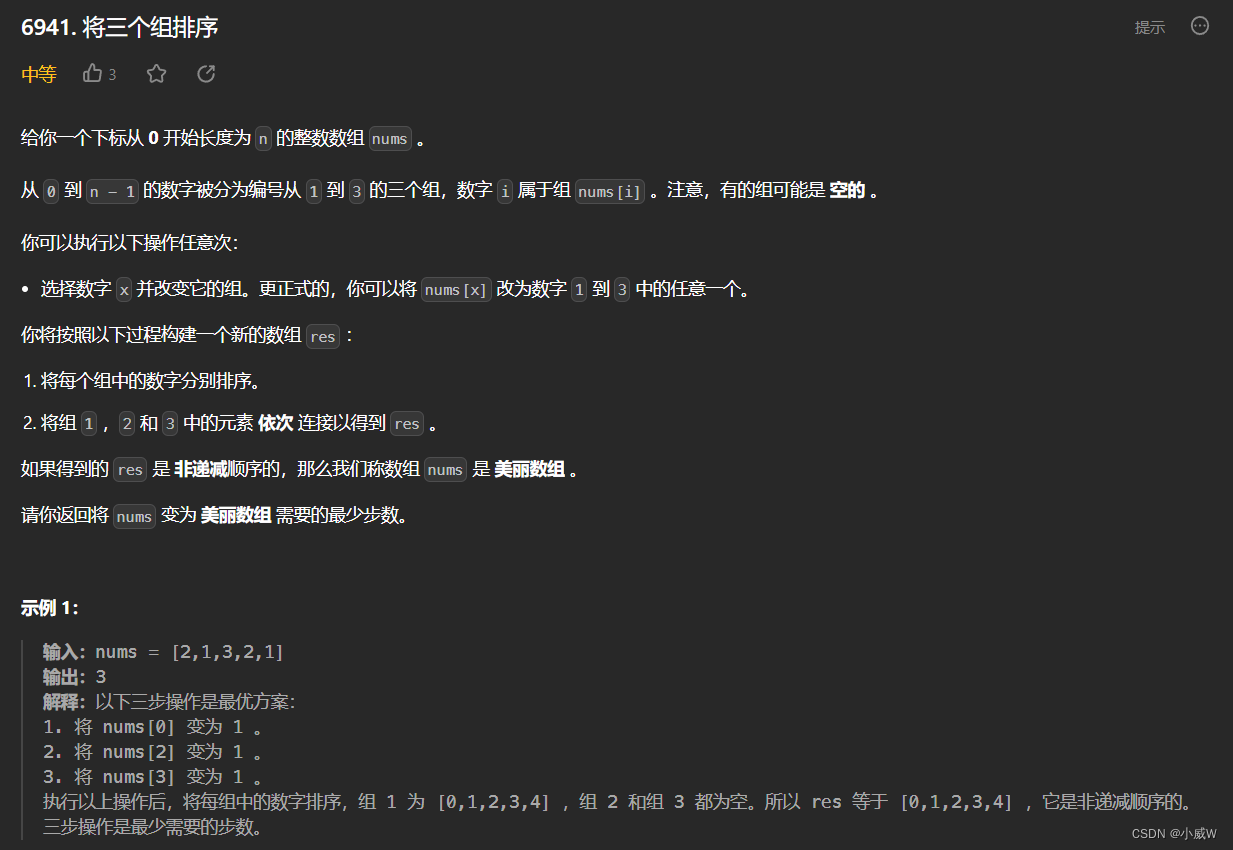
提示：
1 <= nums.length <= 100
1 <= nums[i] <= 3

解法1——转化成最长非递减子序列

转换成最多可以保留多少个元素不变，这些保留的元素必须是非递减的。
那么答案就是除了这些保留的元素之外需要被删去的元素数量。

代码1——$O(n^2)$dp

class Solution {
    public int minimumOperations(List<Integer> nums) {
        int n = nums.size(), ans = 0;
        int[] dp = new int[n];
        for (int i = 0; i < n; ++i) {
            dp[i] = 1;
            for (int j = 0; j < i; ++j) {
                if (nums.get(i) >= nums.get(j)) dp[i] = Math.max(dp[i], dp[j] + 1);
            }
            ans = Math.max(ans, dp[i]);
        }
        return n - ans;
    }
}

代码2——二分写法（更快$O(n\log n)$）

class Solution {
    public int minimumOperations(List<Integer> nums) {
        int n = nums.size();
        List<Integer> g = new ArrayList<>();
        for (int i = 0; i < n; ++i) {
            int l = 0, r = g.size();
            while (l < r) {
                int mid = l + r >> 1;
                if (g.get(mid) <= nums.get(i)) l = mid + 1;
                else r = mid;
            }
            if (l == g.size()) g.add(nums.get(i));
            else g.set(l, nums.get(i));
        }
        return n - g.size();
    }
}

解法2——状态机DP

定义 f[i+1][j] 表示考虑 nums[0] 到 nums[i]，且 nums[i] 变成 j 的最小修改次数。

class Solution {
    public int minimumOperations(List<Integer> nums) {
        int n = nums.size();
        int[][] dp = new int[n + 1][4];
        for (int i = 1; i <= n; ++i) {
            // 从0~i，且nums[i]变成j
            for (int j = 1; j <= 3; ++j) {
                dp[i][j] = dp[i - 1][j];
                // 枚举第 i-1 个数字变成了 k
                for (int k = 1; k < j; ++k) {
                    dp[i][j] = Math.min(dp[i][j], dp[i - 1][k]);
                }
                if (j != nums.get(i - 1)) dp[i][j]++;
            }
        }
        int ans = n;
        for (int j = 1; j <= 3; ++j) {
            ans = Math.min(ans, dp[n][j]);
        }
        return ans;
    }
}

Q4：8013. 范围中美丽整数的数目（数位DP）⭐⭐⭐⭐⭐

https://leetcode.cn/problems/number-of-beautiful-integers-in-the-range/

提示：
0 < low <= high <= 10^9
0 < k <= 20

更多关于数位DP可见：
【算法】数位DP
【算法基础：动态规划】5.4 数位统计DP（计数问题）（数位DP）

解法

代码如下：

class Solution {
    int[][][] memo;
    char[] s;
    int m, k;

    public int numberOfBeautifulIntegers(int low, int high, int k) {
        this.k = k;
        return op(high) - op(low - 1);
    }

    public int op(int n) {
        s = Integer.toString(n).toCharArray();
        m = s.length;
        memo = new int[m][k][m * 2 + 1];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < k; ++j) {
                Arrays.fill(memo[i][j], -1);
            }
        }
        return dfs(0, true, false, 0, m);
    }

    public int dfs(int i, boolean isLimit, boolean isNum, int val, int diff) {
        if (i == s.length) return isNum && val == 0 && diff == m? 1: 0;
        if (!isLimit && isNum && memo[i][val][diff] != -1) return memo[i][val][diff];

        int res = 0;
        if (!isNum) res = dfs(i + 1, false, false, 0, m);
        int up = isLimit? s[i] - '0': 9;
        for (int d = isNum? 0: 1; d <= up; ++d) {
            res += dfs(i + 1, isLimit && d == up, true, (val * 10 + d) % k, diff + d % 2 * 2 - 1);
        }
        if (!isLimit && isNum) memo[i][val][diff] = res;
        return res;
    }
}

使用到的技巧

判断这个数可以被 k 整除

由于是从前往后的，也就是从高位到低位，所以每次执行 (val * 10 + d) % k

判断奇数数位和偶数数位的数量之差

使用 diff 记录两者的数量之差，初始设置为 m，原因是作为数组的下标不能出现负数。
每次执行 diff + d % 2 * 2 - 1) ，这样如果 d 是奇数就会 + 1，否则就会 - 1。

成绩记录

就是很垃圾的成绩了。。。

参考资料

[第111场双周赛]式酱的解题报告