题目描述：


解析：
这道题我想了很多种解决方法，但无一例外都失败了，实在是按照常规线性DP的思路真的想不出来。
看了题解之后才知道它是分为三步解决这个问题的：
第一步：缩小最优解的范围
先用贪心将最优解缩小到某个较小的范围内，再DP求出精确的最优解。
这里就要用到排序不等式了。什么是排序不等式？假设有两个数组，数组a和数组b，满足数组a中的数从小到大递增，数组b中的数从大到小递减，那么a,b两个数组分别相乘之和的最大值一定是a[1]✖b[n]+a[2]✖b[n-1]+…a[n]✖b[1]，最小值一定是a[1]✖b[1]+a[2]✖b[2]+…a[n]✖b[n]。
证明也很简单，就不多说了。
根据排序不等式，我们知道g[i]的值越大，与他相乘的数就要越小，g[i]对应的饼干数也就越大，故本问题的最优解一定在如下的子集中：将所有小朋友按愤怒值g[i]从大到小排序，排名靠前的小朋友分配的饼干要更多一些。
第二步：用DP寻找最优解
此题的状态划分方式与AcWing 900. 整数划分类似，前者是以最小数是不是1来划分，后者是以最后有几个1来划分的。分析图如下所示：

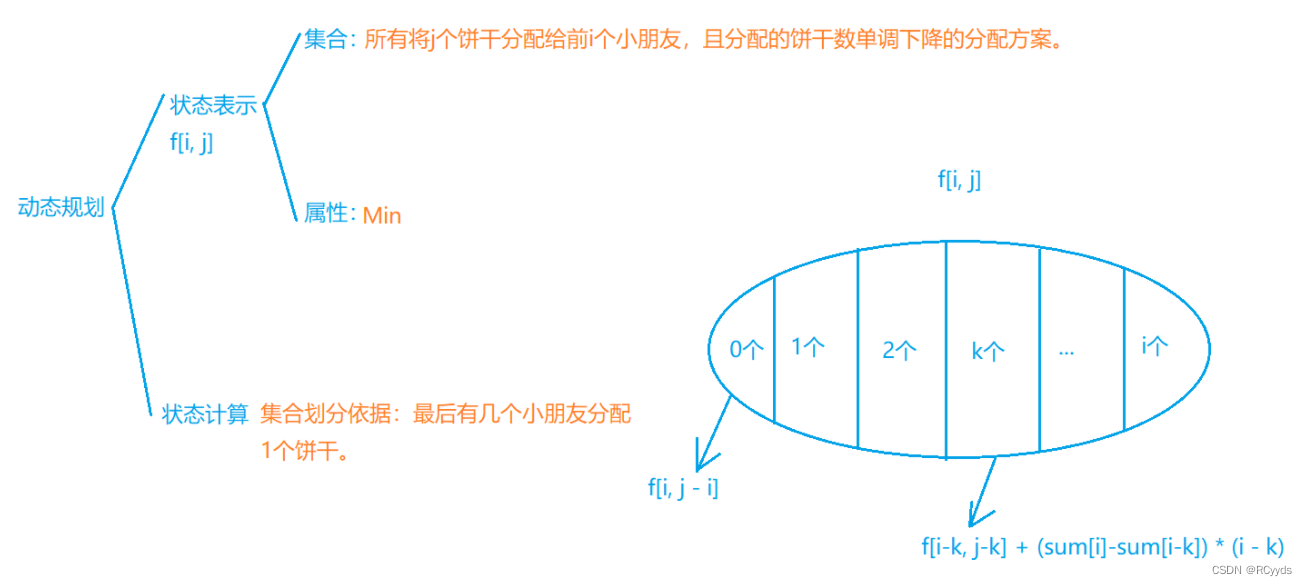
这个划分方法挺难想的，你没做过类似题真难想出来。
现在说说为什么这道题的划分方法与整数划分这道题不一样：写过整数划分这道题的人都知道，这道题有至少两种解决方法，第一种用完全背包问题的思想写，第二种就是以最小数是不是1来划分来写。这第二种方法是定义f[i,j]:总和为i，选的整数个数为j的做法总数，当最小数是1时为f[i-1][j-1]，当最小数不是1时为f[i-j][j]，也就是整体都减1，那么加起来就是f[i][j]了。要注意的是整数划分这道题是求方案数，而我们这道题是求最小值！假如你用整数划分的方法来求会出现什么结果呢？你会发现当最小值是1的情况下，你无法求出最小值，因为你不知道有多少个数大于1，而用最后有几个人分配1个饼干就能完美解决这个问题，就是f[i - k][j - k] + (sum[i] - sum[i - k]) * (i - k)，sum[i]是g[i]排序后的前缀和，而当1的个数为0时，我们就跟整数划分一样，整体都减1，就是f[i][j-i]，然后从中取min就可以了。
初值就先让f全为0x3f3f3f3f，之后让f[0][0]等于0就行了，也就是只能从这个点开始转移。
第三步：倒推求路径
这道题不是求出最值就解决了，你还要将各个小朋友的饼干数的取值也要表示出来，也就是要求路径。
求路径有两种方法，一种是在求的过程中记下路径，这种方法在bfs过程中很常用，另一种就是倒推了，找出每个状态是由哪个状态计算得到的即可。
倒推过程中要注意偏移量h，因为我们在求的过程中可能会有让整体都减1的操作，而且可能会有好几次，那么就要我们在倒推过程中就要加上这个偏移量，不然会出错。

代码：

#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f,N=35,M=5010;
typedef pair<int,int> PII;
PII g[N];
int dp[N][M];
int sum[N],ans[N];
int main()
{
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>g[i].first;
		g[i].second=i;
	}
	sort(g+1,g+1+n);
	reverse(g+1,g+1+n);
	
	for(int i=1;i<=n;i++) sum[i]=sum[i-1]+g[i].first;
	
	memset(dp,0x3f,sizeof dp);
	dp[0][0]=0;
	
	for(int i=1;i<=n;i++)
	{
		for(int j=i;j<=m;j++)
		{
			dp[i][j]=dp[i][j-i];
			for(int k=1;k<=i;k++)
			{
				dp[i][j]=min(dp[i][j],dp[i-k][j-k]+(sum[i]-sum[i-k])*(i-k));
			}
		}
	}
	cout<<dp[n][m]<<endl;
	
	int i=n,j=m,h=0;
	while(i&&j)
	{
		if(j>=i&&dp[i][j]==dp[i][j-i]) j-=i,h++;
		else{
			for(int k=1;k<=i&&k<=j;k++)
			{
				if(dp[i][j]==dp[i-k][j-k]+(sum[i]-sum[i-k])*(i-k))
				{
					for(int u=i;u>i-k;u--)
					ans[g[u].second]=1+h;
					
					i-=k,j-=k;
					break;
				}
				
			}
		}
	}
	for(int i=1;i<=n;i++)
	cout<<ans[i]<<" ";
	return 0;
}