
本文内容借鉴一本我非常喜欢的书——《数据结构与算法图解》。学习之余,我决定把这本书精彩的部分摘录出来与大家分享。
写在前面
算法这个词听起来很深奥,其实不然。它只是解决某个问题的一套流程。
准备一碗麦片的流程也可以说是一种算法,它包含以下 4步(对我来说是 4步吧)。
(1) 拿个碗。
(2) 把麦片倒进碗里。
(3) 把牛奶倒进碗里。
(4) 把勺子放到碗里。
在计算机的世界里,算法则是指某项操作的过程。
上一章我们研究了 4种主要操作,包括读取、查找、插入和删除。
这一章我们还是会经常提到它们,而且一种操作可能会有不止一种做法。也就是说,一种操作会有
多种算法的实现。
我们很快会看到不同的算法能使代码变快或者变慢——高负载时甚至慢到停止工作。不过,现在先
来认识一种新的数据结构:有序数组。它的查找算法就不止一种,我们将会学习如何选出正确的那
种。
1.有序数组
有序数组跟上一章讨论的数组几乎一样,唯一区别就是有序数组要求其值总是保持有序。即每次插
入新值时,它会被插入到适当的位置,使整个数组的值仍然按顺序排列。
以数组 [3,17,80,202] 为例。

假设这是个常规的数组,你准备将 75插入,那就可以把它放到尾端,如下所示。
 如上一章所述,计算机只要 1步就能完成这种操作。
如上一章所述,计算机只要 1步就能完成这种操作。
但如果这是一个有序数组,你就必须要找到一个适当的位置,使插入 75 之后整个数组依然有序。
 做起来可不像说的那么简单。整个过程不可能一步完成,因为计算机需要先找出那个适当的位置,
做起来可不像说的那么简单。整个过程不可能一步完成,因为计算机需要先找出那个适当的位置,
然后将其及以后的值右移来腾出空间给 75。
下面就来介绍分解的步骤。
先回顾一下原始的数组。
第 1步:检查索引 0的值,看 75应该在它的左边还是右边。
因为 75大于 3,所以 75应该在它右边的某个位置。而具体的位置,目前还是不能确定,于是再检查下一个格子。
第 2步:检查下一格的值。
因为 75大于 17,所以继续
第 3步:检查下一格的值。
这次是 80,大于 75。因为这是第一次遇到大于 75的值,可想而知,必须把 75放在 80的左侧以使整个数组维持有序。但要在这里插入 75,还得先将它的位置空出来。
第 4步:将最后一个值右移。
第 5步:将倒数第二个值右移。
第 6步:终于可以把 75插入到正确的位置上了。
可以看到,往有序数组中插入新值,需要先做一次查找以确定插入的位置。这是它跟常规数组的关
键区别(在性能方面)之一。虽然插入的性能比不上常规数组,但在查找方面,有序数组却有着特
殊优势。
2.查找有序数组
上一章介绍了常规数组的查找方式:从左至右逐个格子检查直至找到。这种方式称为线性查找。
接下来看看有序数组的线性查找跟常规数组有何不同。
设一个常规数组 [17,3,75,202,80] ,如果想在里面查找 22(其实并不存在),那你就得逐个元素
去检查,因为 22 可能在任何一个位置上。要想在到达末尾之前结束检查,那么所找的值必须在末
尾之前出现。
然而对于有序数组来说,即便它不包含要找的值,我们也可以提早停止查找。假设要在有序数组
[3,17,75,80,202] 里查找 22,我们可以在查到 75的时候就结束,因为 22不可能出现在 75的右边。
以下是用C语言实现的有序数组线性查找。
int Search(int arr[], int sz,int val)
{
//遍历数组的每个元素
for (int i = 0; i < sz; i++)
{
if (arr[i] > val)
{
return -1;
}
if (arr[i] == val)
{
//找到了,返回val的索引
return i;
}
}
//找不到,返回-1
return -1;
}因此,有序数组的线性查找大多数情况下都会快于常规数组。除非要找的值是最后那个,或者比最
后的值还大,那就只能一直查到最后了。
只看到这里的话,可能你还是不会觉得两种数组在性能上有什么巨大区别。
这是因为我们还没释放算法的潜能。这是接下来就要做的
今天我们提到的查找有序数组的方法就只有线性查找。但其实,线性查找只不过是查找算法的其中
一种而已。这种逐个格子检查直至找到为止的过程,并不是查找的唯一途径。
有序数组相比常规数组的一大优势就是它可以使用另一种查找算法。此种算法名为二分查找,它比
线性查找要快得多。
3.二分查找
你小时候或许玩过这样一种猜谜游戏(或者现在跟你的小孩玩过):我心里想着一个 1到 100之间
的数字,在你猜出它之前,我会提示你的答案应该大一点还是小一点。
你应该凭直觉就知道这个游戏的策略。一开始你会先猜处于中间的 50,而不是 1。为什么?
因为不管我接下来告诉你更大或是更小,你都能排除掉一半的错误答案!
如果你说 50,然后我提示要再大一点,那么你应该会选 75,以排除掉剩余数字的一半。如果在
75之后我告诉你要小一点,你就会选 62或 63。总之,一直都猜中间值,就能不断地缩小一半的范
围。
下面来演示这个过程,但仅以 1到 10为例。
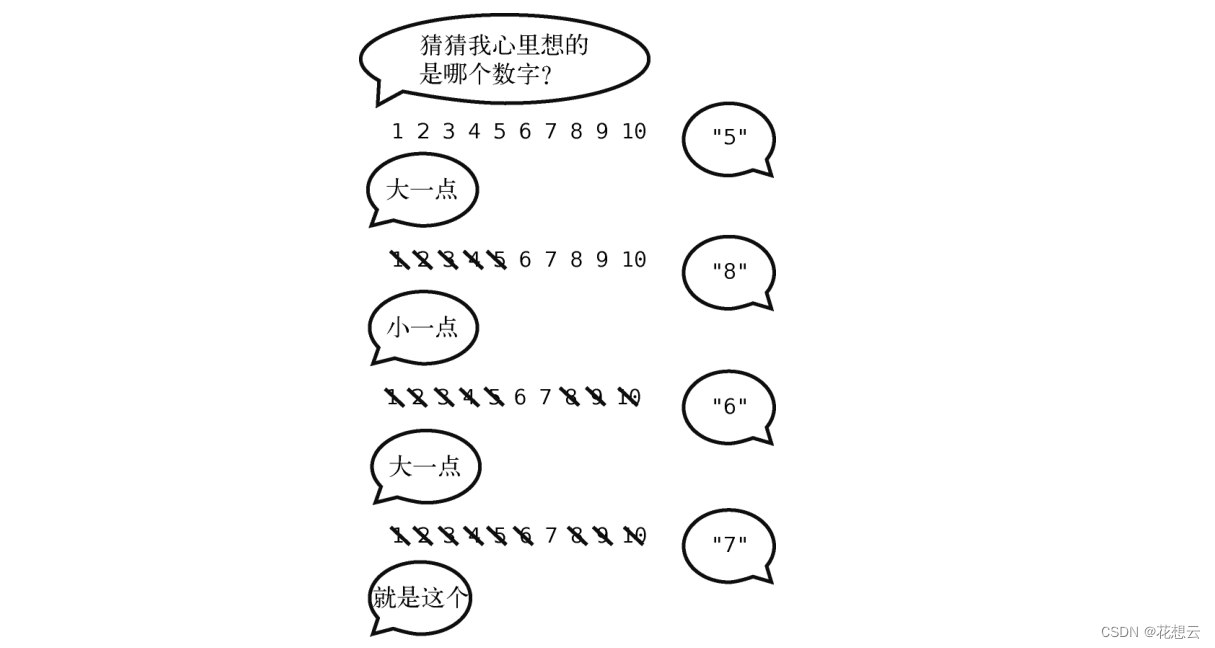
这就是二分查找的通俗描述。
有序数组相比常规数组的一大优势就是它除了可以用线性查找,还可以用二分查找。常规数组因为
无序,所以不可能运用二分查找。 为了看出它的实际效果,假设有一个包含 9个元素的有序数组。
计算机不知道每个格子的值,如下图所示。

然后,用二分查找来找出 7,过程如下。
第 1步:检查正中间的格子。因为数组的长度是已知的,将长度除以 2,我们就可以跳到确切的内
存地址上,然后检查其值。
 值为 9,可推测出 7应该在其左边的某个格子里。而且,这下我们也排除了一半的格子,即 9右边
值为 9,可推测出 7应该在其左边的某个格子里。而且,这下我们也排除了一半的格子,即 9右边
的那些(以及 9本身)。

第 2步:检查 9左边的那些格子的最中间那个。因为这里最中间有两个,我们就随便挑了左边的。
 它的值为 4,那么 7就在它的右边了。由此 4左边的格子也就排除了。
它的值为 4,那么 7就在它的右边了。由此 4左边的格子也就排除了。

第 3步:还剩两个格子里可能有 7。我们随便挑个左边的。
 第 4步:就剩一个了。(如果还没有,那就说明这个有序数组里真的没有 7。)
第 4步:就剩一个了。(如果还没有,那就说明这个有序数组里真的没有 7。)
 终于找到 7了,总共 4步。是的,这个有序数组要是用线性查找也会是 4步,但稍后你就会见识到
终于找到 7了,总共 4步。是的,这个有序数组要是用线性查找也会是 4步,但稍后你就会见识到
二分查找的强大。
以下是二分查找的 C语言实现。
int Search(int arr[], int sz, int val)
{
int left = 0; //定义一个左指针
int right = sz - 1; //定义一个右指针
while (left <= right)
{
int mid = left+(right-left) / 2; //防止越界
if (arr[mid] == val) //找到了,返回下标
{
return mid;
}
if (arr[mid] < val)
{
left = mid + 1; //让mid+1成为新的左指针
}
if (arr[mid] > val)
{
right = mid - 1; //让mid-1成为新的右指针
}
}
return -1; //没找到,返回-1
}4.二分查找与线性查找
对于长度太小的有序数组,二分查找并不比线性查找好多少。但我们来看看更大的数组。
对于拥有 100个值的数组来说,两种查找需要的最多步数如下所示。
线性查找:100步
二分查找:7步
用线性查找的话,如果要找的值在最后一个格子,或者比最后一格的值还大,那么就得查遍每个格
子。有 100个格子,就是 100步。
二分查找则会在每次猜测后排除掉一半的元素。100 个格子,在第一次猜测后,便排除了50 个。
再换个角度来看,你就会发现一个规律。
长度为 3的有序数组,二分查找所需的最多步数是 2。
若长度翻倍,变成 7(以奇数为例会方便选择正中间的格子,于是我们把长度翻倍后又增加
了一个数),则最多步数会是 3。
若再翻倍(并加 1),变成 15个元素,那么最多步数会是 4
规律就是,每次有序数组长度乘以 2,二分查找所需的最多步数只会加 1。
这真是出奇地高效。
相反,在 3 个元素的数组上线性查找,最多要 3 步,7 个元素就最多要 7 步,100 个元素就最多要
100步,即元素有多少,最多步数就是多少。数组长度翻倍,线性查找的最多步数就会翻倍,而二
分查找则只是增加 1 步。
这种规律可以用下图来展示。
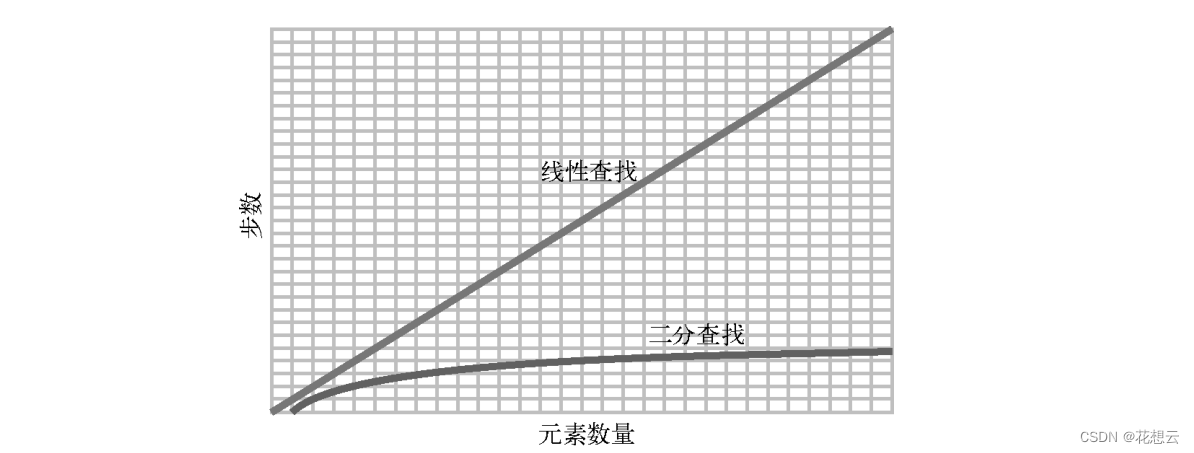
如果数组变得更大,比如说 10 000个元素,那么线性查找最多会有 10 000步,而二分查找最多只
有 14步。再增大到 1 000 000个元素,则线性查找最多有 1 000 000步,二分查找最多只有 20
步。
总结
关于算法的内容就是这些。很多时候,计算一样东西并不只有一种方法,换种算法可能会极大地影
响程序的性能。
同时你还应意识到,世界上并没有哪种适用于所有场景的数据结构或者算法。你不能因为有序数组
能使用二分查找就永远只用有序数组。在经常插入而很少查找的情况下,显然插入迅速的常规数组
会是更好的选择。





















![[附源码]Node.js计算机毕业设计高校医疗健康服务系统的设计与实现Express](https://img-blog.csdnimg.cn/d64c75d077ea4ec295cbe91fa10b49f2.png)
