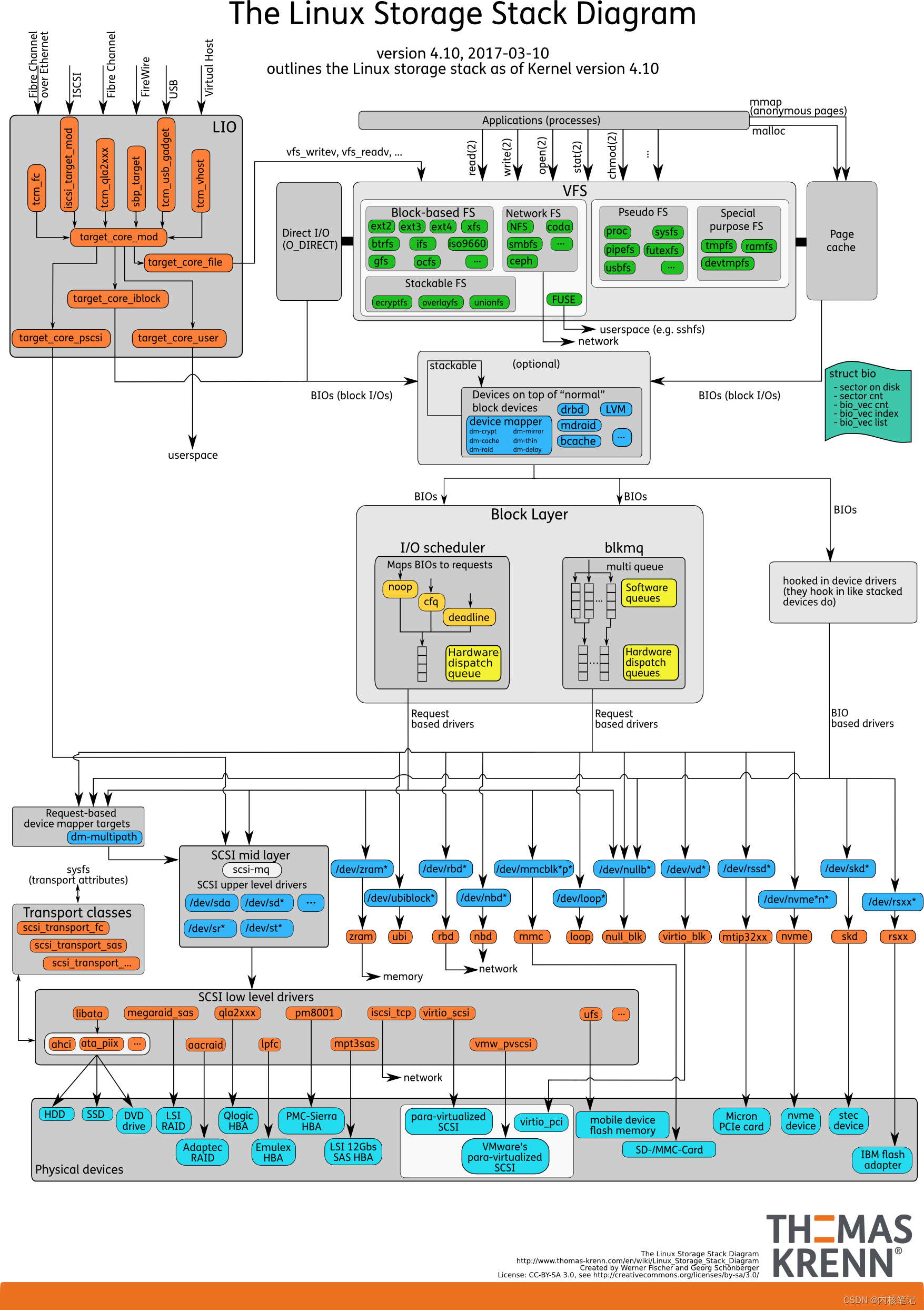
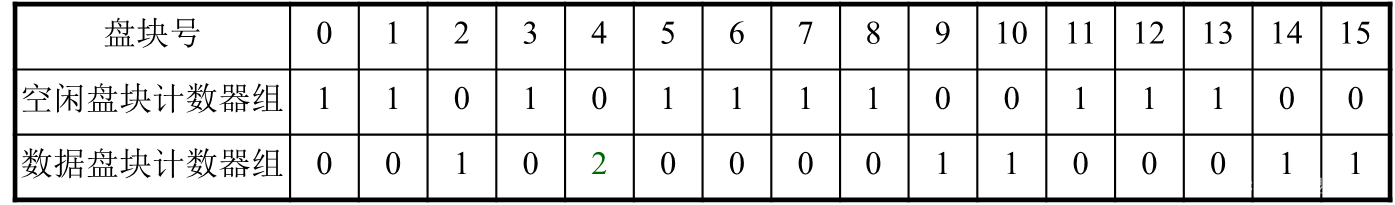RK3399平台开发系列讲解(存储篇)Linux 存储系统的 I/O 栈
news2026/2/8 14:58:59
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/936611.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
vue2 路由进阶,VueCli 自定义创建项目
一、声明式导航-导航链接
1.需求
实现导航高亮效果 如果使用a标签进行跳转的话,需要给当前跳转的导航加样式,同时要移除上一个a标签的样式,太麻烦!!!
2.解决方案
vue-router 提供了一个全局组件 router…
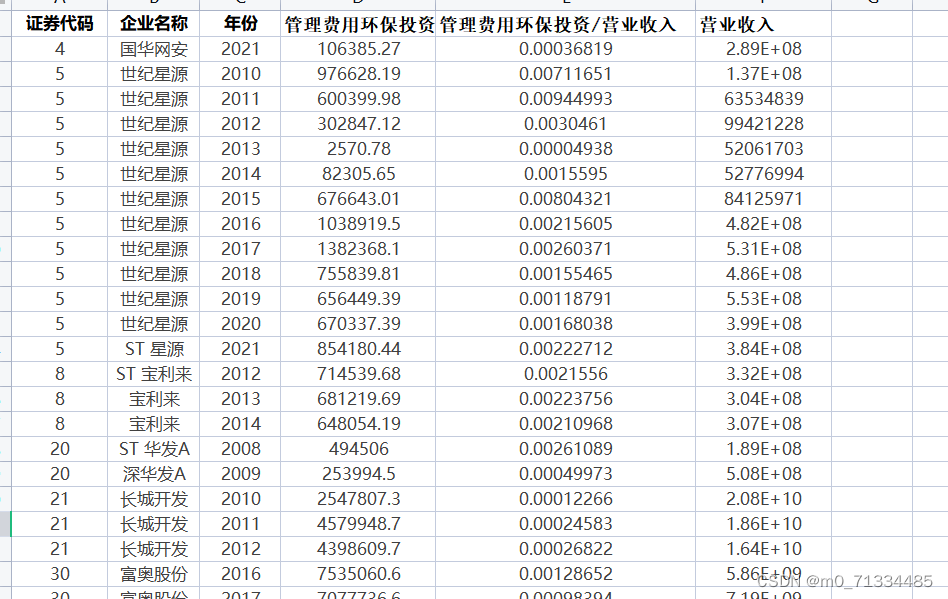
2000-2021年上市公司绿色投资环保投资与营业收入之比数据(原始数据+计算代码+计算结果)
2000-2021年上市公司绿色投资环保投资与营业收入之比数据(原始数据计算代码计算结果)
1、时间:2000-2021年
2、来源:上市公司年报
3、指标:证券代码、企业名称、年份、管理费用环保投资、管理费用环保投资/营业收入…
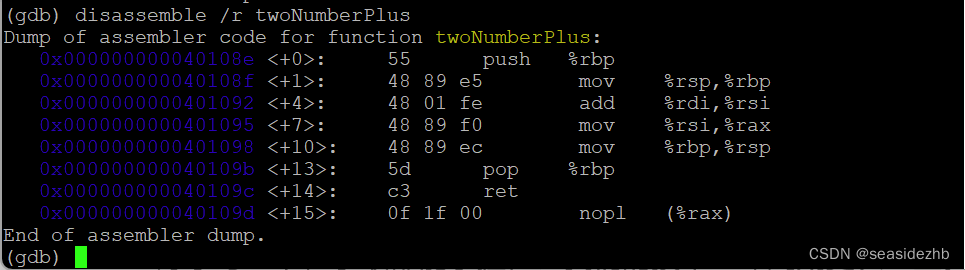
ARTS打卡第二周之链表环的检测、gdb中disassemble的使用、底层学习建议、学习分享
Algorithm
题目:链表中环的检测 自己的分析见博客《检测链表中是否存在环》
Review
disassemble command是我读的一篇英语文章,这篇文章主要是介绍gdb反汇编命令的使用和参数。自己为了能够演示这篇文章里边的内容,特意自己使用汇编语言编…
枫叶时代:《超能一家人》喜剧电影引发观众无限笑点
近期,由浙江开心麻花影业有限公司、中国电影股份有限公司和上海阿里巴巴影业有限公司三家公司联合出品的喜剧电影《超能一家人》引起了观众们的热烈关注。这部影片由宋阳导演执导,他曾执导过备受好评的作品《羞羞的铁拳》。时长108分钟的《超能一家人》以…
Modbus转Profinet网关与流量变送器兼容转ModbusTCP协议博图配置
首先,我们需要明确电磁流量计的通信协议是Modbus,而西门子1200PLC的通信协议是Profinet。这两种协议在功能和特性上存在一定的差异,因此需要使用兴达易控Modbus转Profinet网关设备进行转换。兴达易控的XD-MDPN100是Profinet转ModbusTCP的网关…
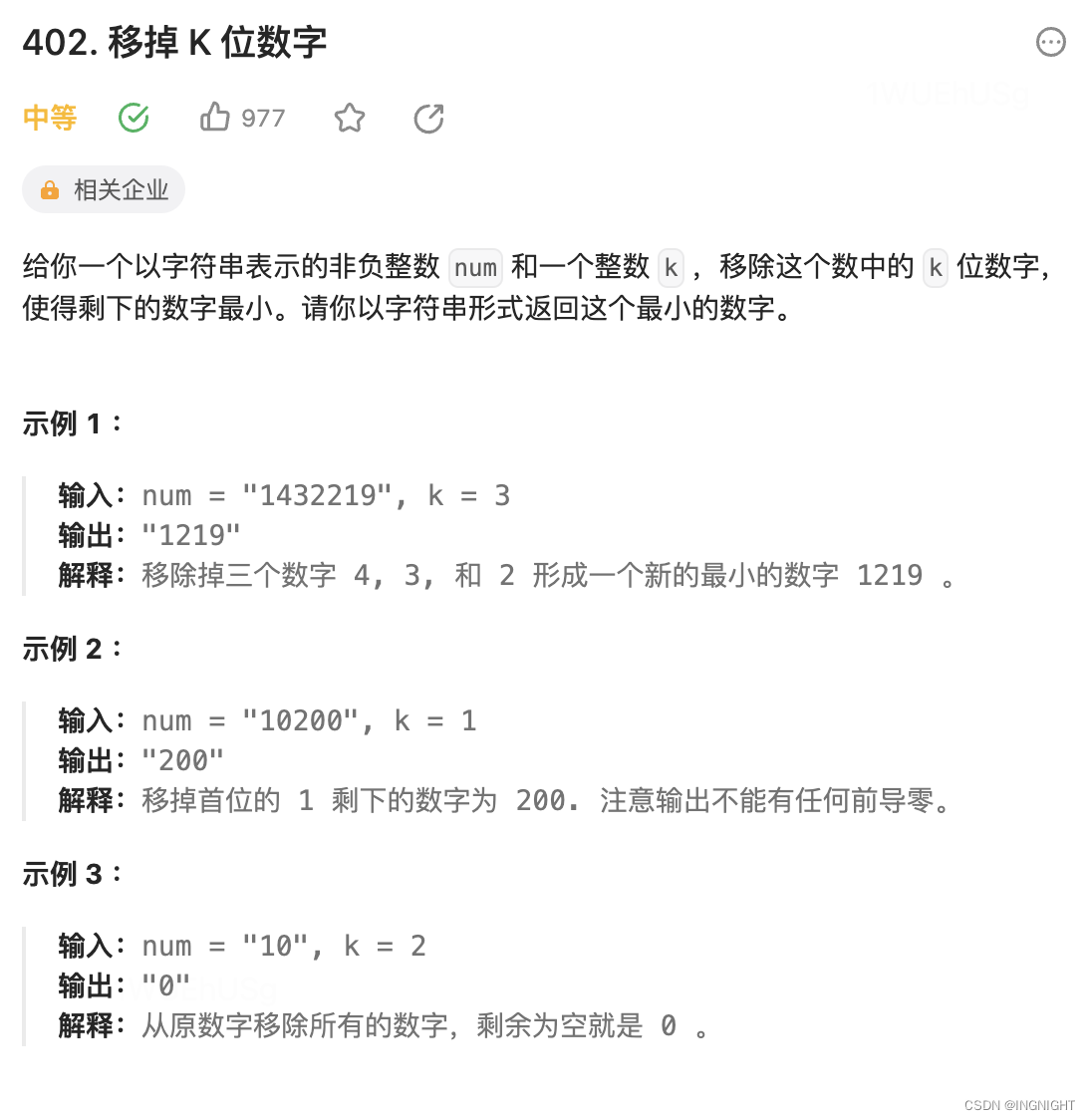
402. 移掉 K 位数字
链接:
402. 移掉 K 位数字
题解:
class Solution {
public:string removeKdigits(string num, int k) {vector<char> stk;for (auto& digit: num) {while (stk.size() > 0 && stk.back() > digit && k) {stk.pop_bac…
Adobe Illustrator 2023 for mac安装教程,可用。
Adobe Illustrator 是行业标准的矢量图形应用程序,可以为印刷、网络、视频和移动设备创建logos、图标、绘图、排版和插图。数以百万计的设计师和艺术家使用Illustrator CC创作,从网页图标和产品包装到书籍插图和广告牌。此版本是2023版本,适配…
LeetCode-455-分发饼干-贪心算法
题目描述: 假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。 对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 jÿ…
002微信小程序云开发API数据库-迁移状态查询/更新索引
文章目录 微信小程序云开发API数据库-迁移状态查询案例代码微信小程序云开发API数据库-更新索引案例代码 微信小程序云开发API数据库-迁移状态查询
在微信小程序中,云开发API数据库是一种方便快捷的数据库解决方案。但是,有时候我们可能需要将云开发数据…
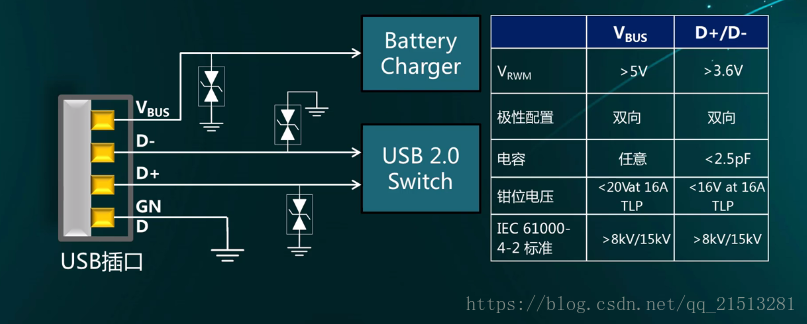
单片机TVS/ESD二极管防护
TVS 瞬态电压抑制二极管Transient Voltage Suppressor
ESD 静电释放二极管 Electro-Static discharge
这两种本质上都是二极管。都是利用了二极管正向导通、反向截止的特性。二极管在反向截止截止条件下,如果电压继续增大,将会引发雪崩,使得…
【C语言基础】牛客题库练习第(一)期
📢:如果你也对机器人、人工智能感兴趣,看来我们志同道合✨ 📢:不妨浏览一下我的博客主页【https://blog.csdn.net/weixin_51244852】 📢:文章若有幸对你有帮助,可点赞 👍…
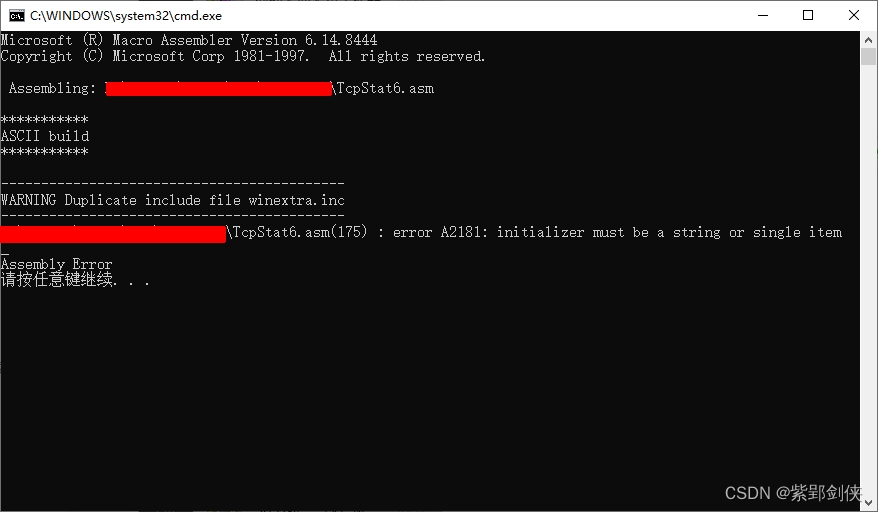
解决MASM32代码汇编出错: error A2181: initializer must be a string or single item
最近用MASM32编程更新SysInfo,增加对IPv6连接信息的收集,使用到了
typedef struct _MIB_TCP6ROW_OWNER_MODULE {UCHAR ucLocalAddr[16];DWORD dwLocalScopeId;DWORD dwLocalPort;UCHAR ucRemoteAddr[16];DWORD …
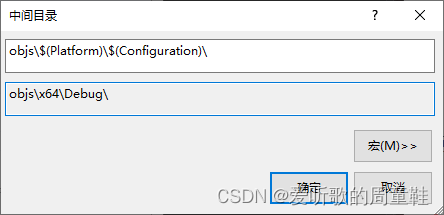
Visual Studio 2017安装和项目配置
目录 前言1. What、Why and How1.1 What1.2 Why1.3 How 2. 安装3. 创建新项目4. 配置OpenCV库4.1 下载opencv安装包4.2 配置系统环境变量4.3 VS项目环境配置4.4 总结 5. 已有项目添加6. Tips6.1 常用快捷键6.2 字体和颜色选择6.3 配置编译路径 结语下载链接参考 前言 最近因为项…
操作系统期末复习合集——第六章:文件管理
操作系统期末复习合集——第六章:文件管理 引言6.1 文件和文件系统一、文件1. 有结构文件2. 无结构文件(流式文件) 二、文件系统1. 功能2. 文件系统接口 6.2 文件的逻辑结构一、文件结构二、文件逻辑结构的类型三、顺序文件1. 排序2. 读/写3.…
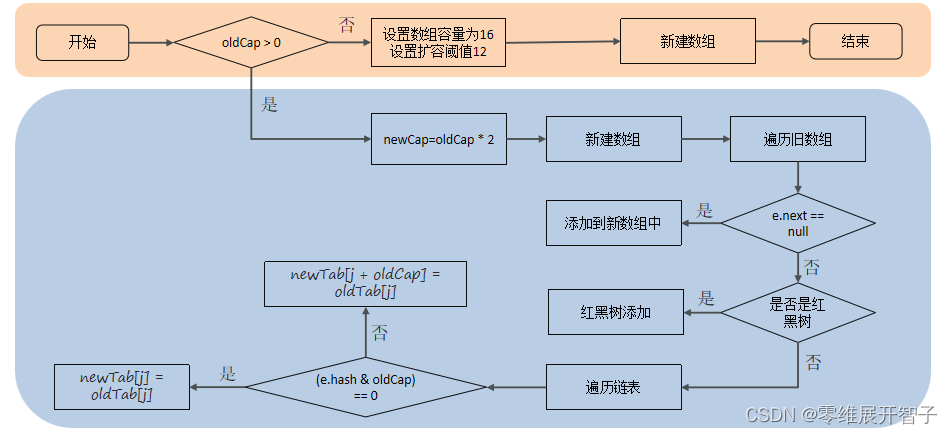
Java后端开发面试题——集合篇
ArrayList底层的实现原理是什么
底层数据结构
ArrayList底层是用动态的数组实现的
初始容量
ArrayList初始容量为0,当第一次添加数据的时候才会初始化容量为10
扩容逻辑
ArrayList在进行扩容的时候是原来容量的1.5倍,每次扩容都需要拷贝数组 添加逻…
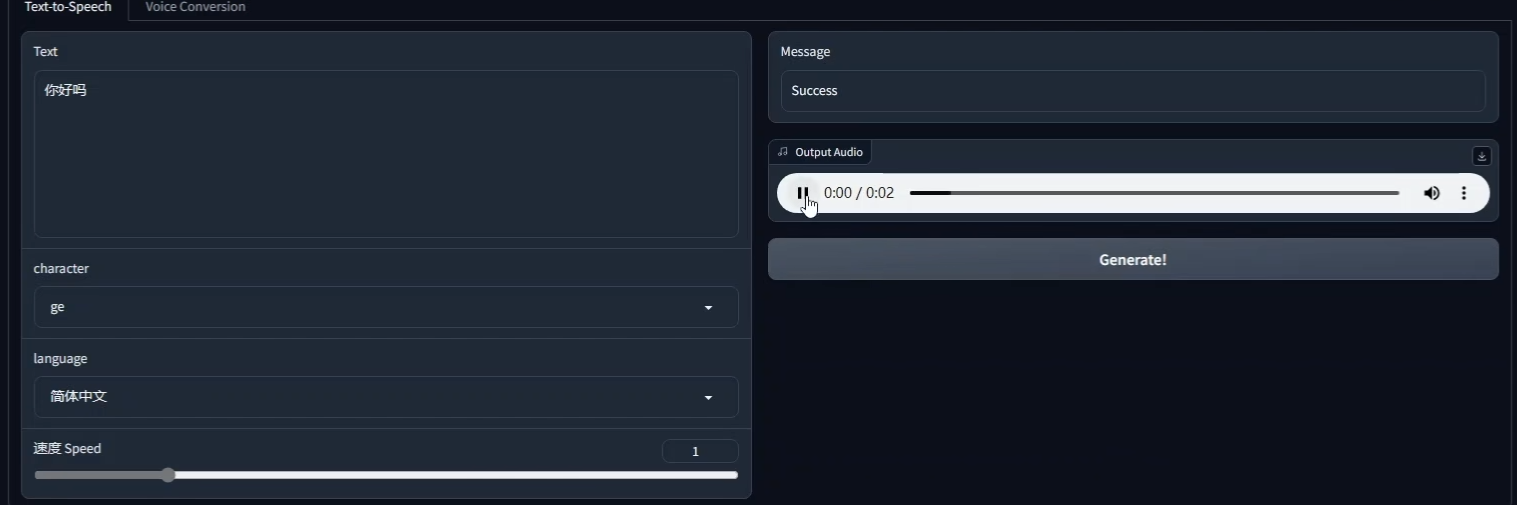
最强嘴提o.o文字转语音
下载
链接:https://pan.baidu.com/s/1cb24WW2dihtRpMz4giMxyw 提取码:k3xu 解压密码:领航员未鸟
项目源码:https://github.com/Plachtaa/VITS-fast-fine-tuning/tree/main
使用
解压后来到,该目录下,把…
在云原生环境中构建可扩展的大数据平台:方法和策略
文章目录 1. **选择适当的云提供商:**2. **采用容器化和微服务架构:**3. **分层架构设计:**4. **弹性计算资源:**5. **使用分布式计算框架:**6. **数据分区和分片:**7. **使用列式存储:**8. **缓…
JS 常见的 6 种继承方式
原型链继承
原型链继承是比较常见的继承方式之一,其中涉及的构造函数、原型和实例,三者之间存在着一定的关系,即每一个构造函数都有一个原型对象,原型对象又包含一个指向构造函数的指针,而实例则包含一个原型对象的指…
On-Manifold Optimization: Local Parameterization
Overview
Manifold Space vs Tangent Space Jacobian w.r.t Error State
Jacobian w.r.t Error State vs True State
According 1 2.4, The idea is that for a x ∈ N x \in N x∈N the function g ( δ ) : f ( x ⊞ δ ) g(\delta) : f (x \boxplus \delta) g(δ):f(x…