基本概念

孪生网络（Siamese Network）是一类神经网络结构，它是由两个或更多个完全相同的网络组成的。孪生网络通常被用于解决基于相似度比较的任务，例如人脸识别、语音识别、目标跟踪等问题。

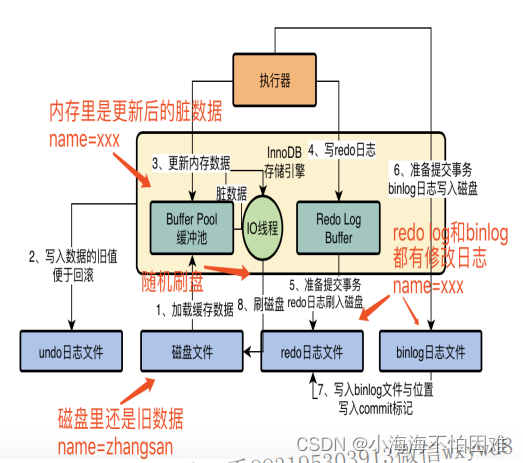
孪生网络的基本思想是将输入数据同时输入到两个完全相同的神经网络中，这两个网络共享相同的权重和参数。通过学习输入数据在这两个网络中的表示，孪生网络可以计算出两个输入样本之间的相似度。处理过程如下：

1. 将两个输入样本通过各自的神经网络得到两个表示向量。
2. 使用一种度量方法（例如欧氏距离、余弦相似度等）计算这两个向量之间的相似度得分。
3. 根据相似度得分进行分类或回归等操作。

细节

训练一个孪生网络首先要有一个大的分类数据集，数据有标注，每一类下面有很多的样本。比如下面的数据集有5类，分别是哈士奇，大象，老虎，鹦鹉，汽车。

基于这个训练集，我们要构造正样本（Positive Samples）和负样本（Negative Samples）。正样本可以告诉神经网络哪些事物是同一类，负样本可以告诉神经网络事物之间的区别。给正样本打上标签1表示同一类，负样本打上标签0表示不同类。如下图所示，这些样本都是从上面的分类数据集里随机抽样出来的。

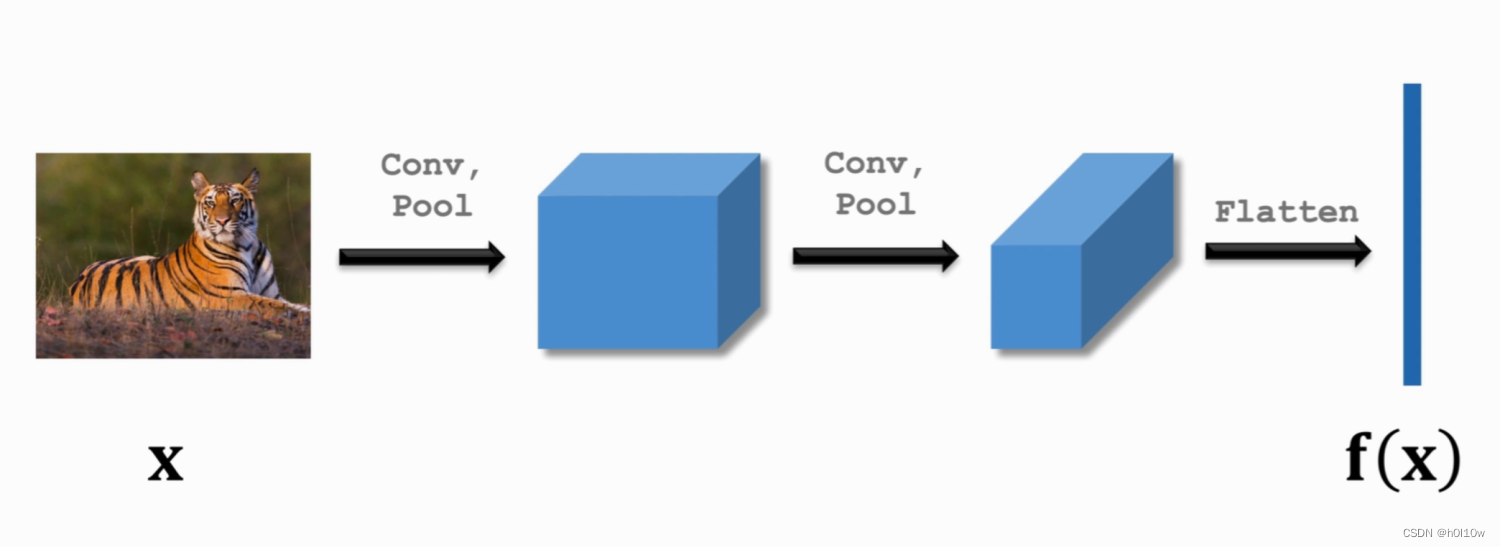
然后我们可以搭一个神经网络来提取特征（比如做两次卷积），最后得到特征向量$f(x)$。

将输入的$x_1$和$x_2$送入我们搭建的神经网络$f(\cdot )$，得到特征向量$h_1$和$h_2$；然后将这两个向量相减再求绝对值，得到向量$z=\left|h_1-h_2\right|$，表示这两个向量之间的区别；再通过一个或一些全连接层，最后用Sigmoid激活函数将值映射到0到1之间。

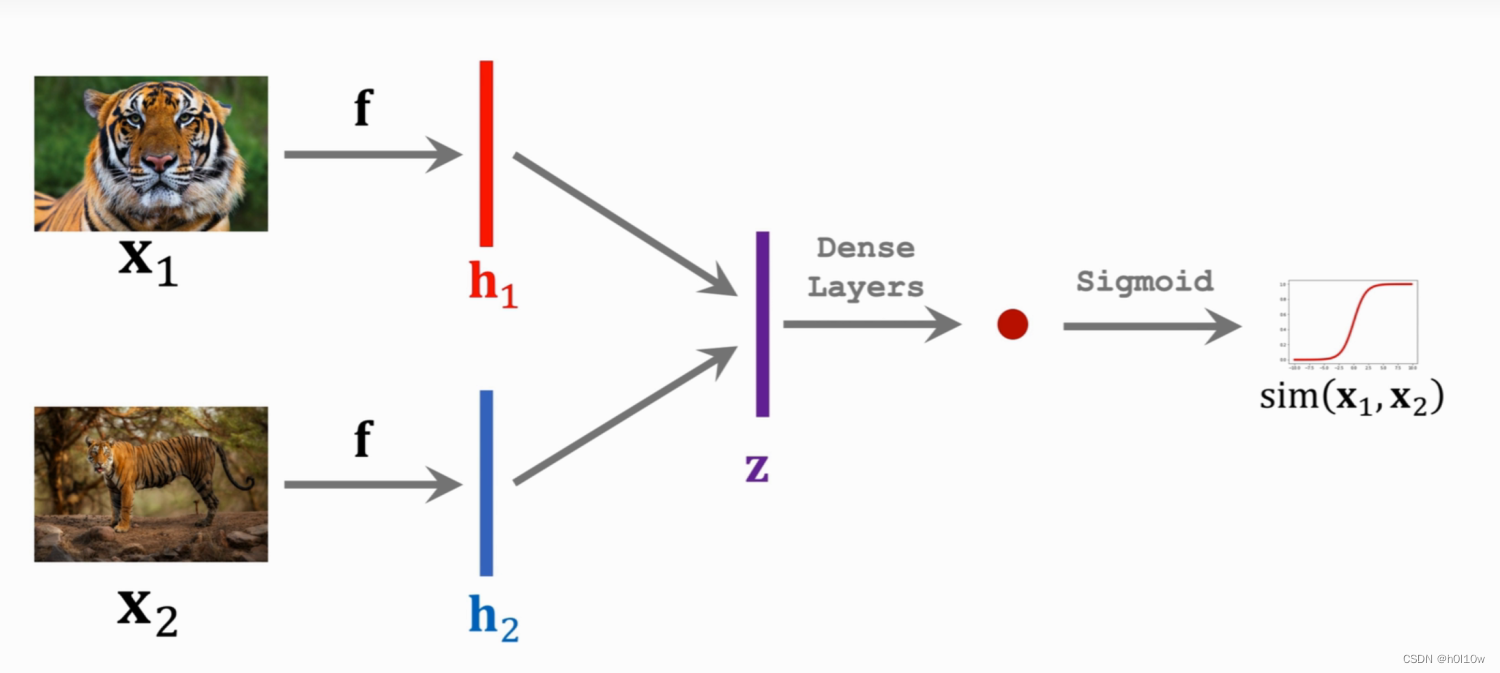
这个最终的输出$sim(x_1,x_2)$就可以用来衡量两个图片之间的相似度（Similarity）。如果两个图片相似，输出应该接近1；如果不同，则应该接近0。

上面提到过样本是有标签的，1表示同一类，0表示不同类。结合标签和刚才的输出$sim(x_1,x_2)$就能选择一个损失函数Loss来计算损失，接着就是老一套的梯度下降和反向传播。反向传播首先更新全连接层的参数，然后进一步传播到卷积层的参数，如下图所示。

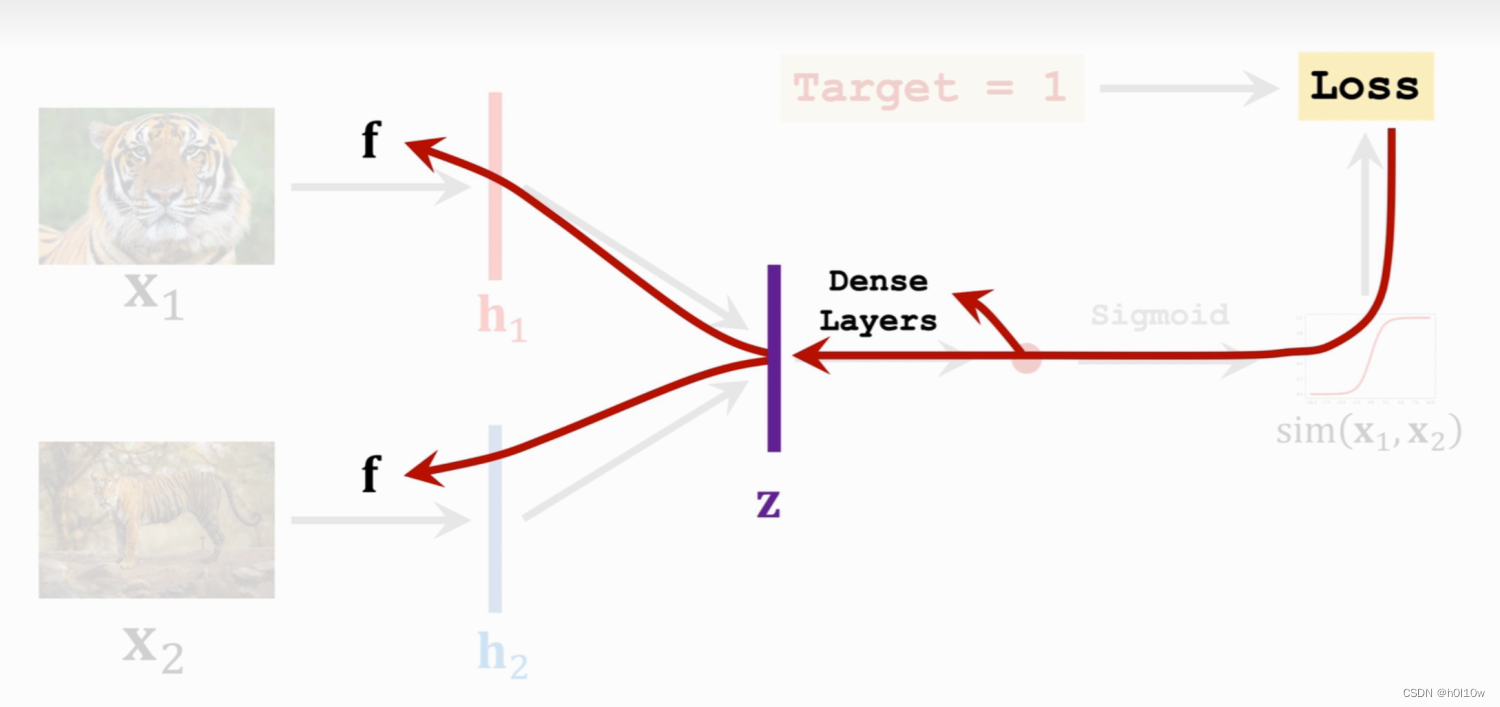
通过不断的迭代，最终得到一个效果较好的网络。通过这个网络，我们就可以让机器具有对比事物的能力，为后续的小样本学习奠定基础。

Triplet Loss

Triplet Loss是另一种训练Siamese Network的方法。它也需要有和上面一样的分类数据集。基于这个数据集，我们需要构造一个三元组。从数据集里随机选取一个图片作为锚点$x^a$（anchor），然后在和它相同类别的数据中随机选一个不同的图片作为正样本$x^{+}$（positive），在不同类别的数据中随机选一个作为负样本$x^{-}$（negative）。

和前面一种方法一样，得到三元组的样本之后也通过一个神经网络提取特征，分别得到特征向量$f(x^{+}),f(x^a),f(x^{-})$。然后分别计算正样本和负样本与锚点之间的距离（二范数的平方），得到$d^{+}$和$d^{-}$。整个过程如下图所示。

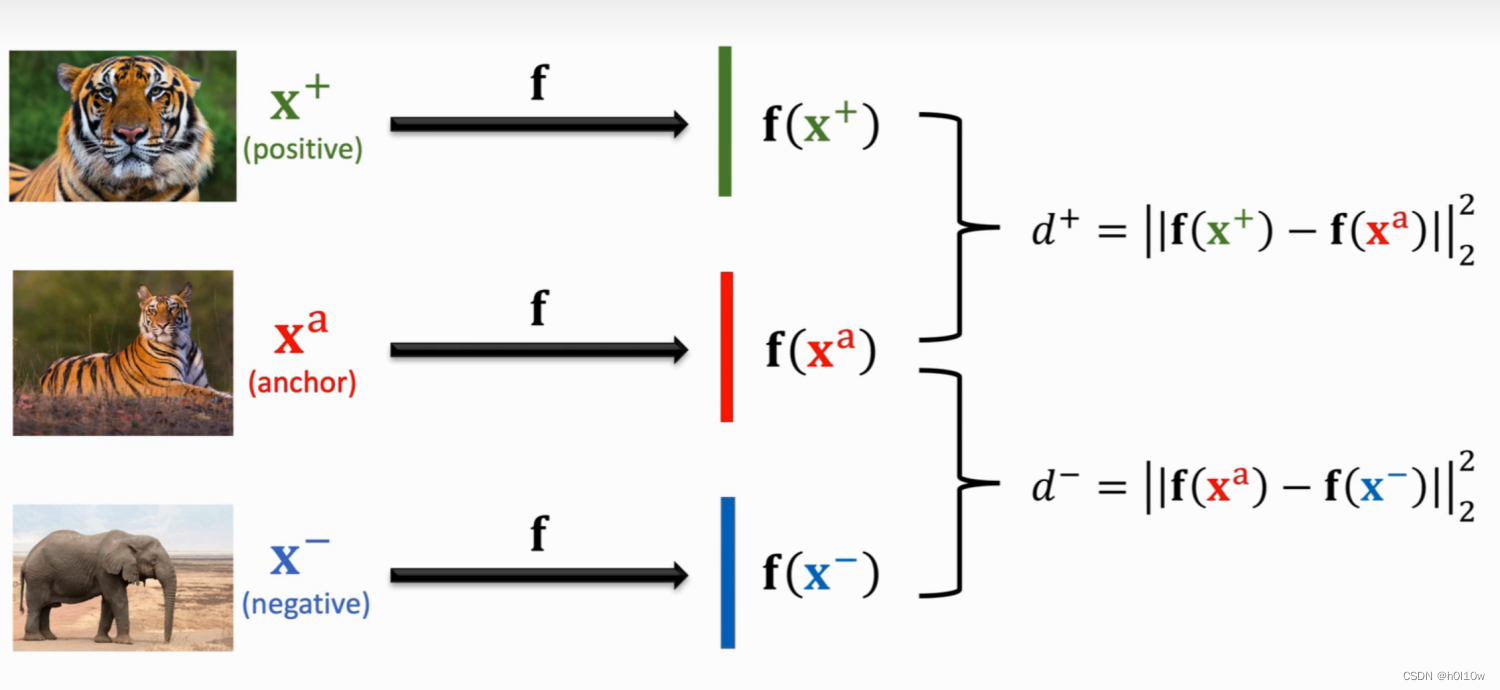
由于正样本和锚点是同一类，所以$d^{+}$应该小；负样本和锚点是不同类，$d^{-}$应该大。并且$d^{+}$要尽可能小，$d^{-}$要尽可能大，使得他们容易区分。呈现在特征空间里就是下面这个样子。

基于上面这种想法，我们可以得到$d^{-}\ge d^{+}+margin(margin>0)$，然后就可以定义损失函数$Loss=max(d^{+}-d^{-}+margin,0)$。当$d^{+}$明显小，$d^{-}$明显大时，这就是我们所追求的目标，没必要让梯度再更新了。此时max的第一项小于0，整体Loss等于0，正好梯度不会变化。当$d^{+}$和$d^{-}$接近甚至大于时，Loss保留的就是第一项的正值，于是就会让梯度继续更新，寻求一个更小值。

至于为什么要设置margin，是为了避免模型走捷径，将负样本和正样本的嵌入向量训练成很相近。因为如果没margin，只要$d^{+}=d^{-}$ 就可以让Loss一直为0，一直满足训练目标，但此时模型很难正确区分正例和负例。