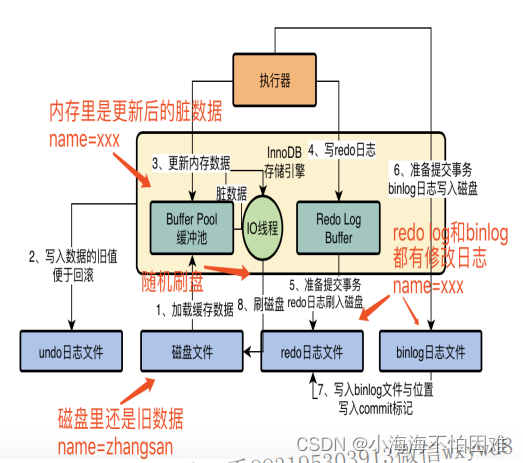
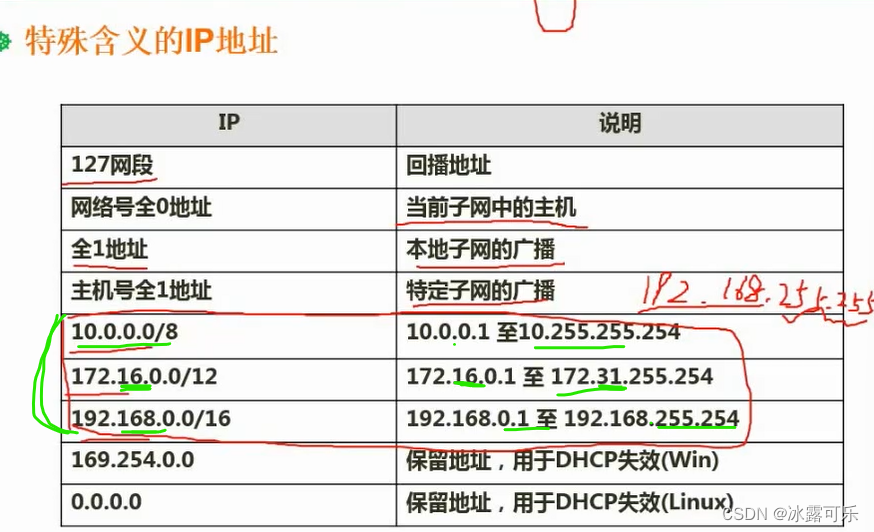
题目描述：

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一

棵树的中序遍历，请构造二叉树并返回其根节点。

题目要求：

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• preorder 和 inorder 均 无重复 元素
• inorder 均出现在 preorder
• preorder 保证 为二叉树的前序遍历序列
• inorder 保证 为二叉树的中序遍历序列

示例1：

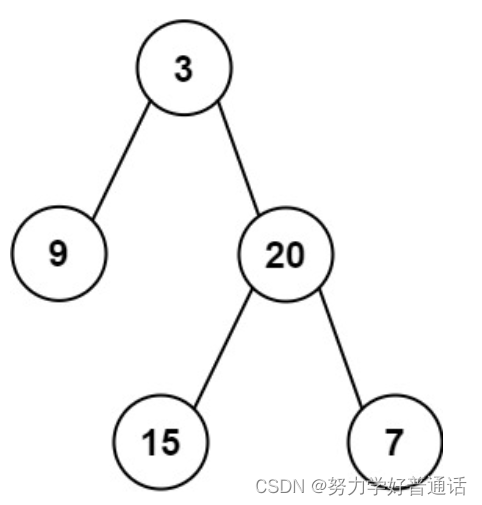
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

 示例二：

输入: preorder = [-1], inorder = [-1]
输出: [-1]

题目分析：

题目要求通过前序遍历和中序遍历来构造二叉树，首先得明白前序遍历，分别是根，左子树，右子

树，中序遍历则是左子树根右子树，如此便有迹可循了，首先通过前序遍历可以确定二叉树的根，

再通过中序遍历来确定左子树和右子树，再通过递归遍历来构成二叉树。 

问题实现：

前序遍历：根     左子树     右子树   （用来确定根）

中序遍历：左子树     根     右子树   （用来确定左右区间）

假设root为根，从前序遍历的第一个元素，通过root，根据中序遍历，可分为

[begin,root-1]  root  [root+1,end]

之后再将前序遍历中的下一个元素作为root，再进行递归遍历左子树和右子树

实现的代码如下：

class Solution {
public:

    TreeNode* _build(vector<int>& preorder, vector<int>& inorder,int& prei,int inbegin,int inend) 
    {
        if(inbegin > inend)
        {
            return nullptr;
        }

        TreeNode* root = new TreeNode(preorder[prei]);
        int rooti = inbegin;
        while(rooti <= inend)
        {
            if(preorder[prei] == inorder[rooti])
            {
                break;
            }
            ++rooti;
        }

        ++prei;
        root->left = _build(preorder,inorder,prei,inbegin,rooti-1);
        root->right = _build(preorder,inorder,prei,rooti+1,inend);
        return root;
    }

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int prei = 0;
        int inbegin = 0;
        int inend = inorder.size() - 1;
        return _build(preorder,inorder,prei,inbegin,inend);
    }
};

 现在根据示例1来进行递归展开图：

 

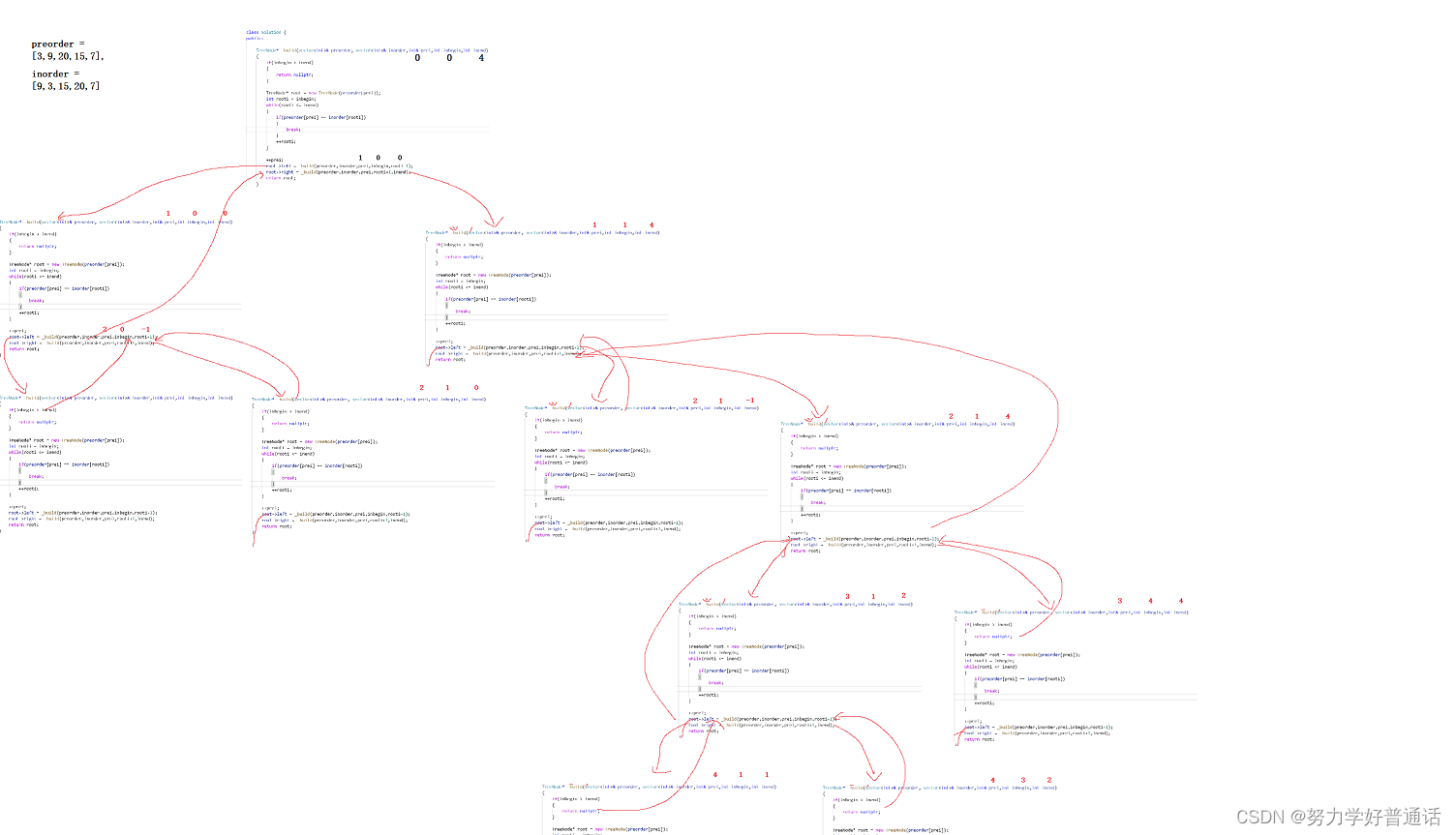
这就是对应的实现。