在开始之前，我们先说一下信息熵的概念。

当一件事情发生，如果是意料之中，那么这个事情就并不能拿来当做茶余饭后的谈资，我们可以说这个事情并没有什么信息和价值。而当一件不可能发生的事情发生的时候，我们可能就会觉得震撼三观，这件事情太Crazy了，带来的信息量也就很多。

哼哼，通过上文我们可以知道，一个事情越稳定，信息量就越少，那么如何去衡量呢？我们可以用概率的倒数（也就是负相关）来衡量。
$$I=-log(p(x))$$
$I$也就是自信息，一件事情越确定，自信息也就越小。

而信息熵就是自信息的期望，代表这一件事情的混乱程度。信息熵越大，混乱程度越大，说明这件事情越疯狂。
$$H=-log(p(x))p(x)$$

---

再说熵权法(Entropy Weight Method)，熵权法是客观赋权的一种方式，对应的主观赋权有专家打分法，相似的还有层次分析法。熵权法是利用信息稳定程度而提出的方法，一般来说，某列属性越稳定，它的信息就越可信，那么在实际的权重也应当越高。

不说人话，那就是：

一般来说，若某个指标的信息熵越小，表明指标值得变异程度越大，提供的信息量越多，在综合评价中所能起到的作用也越大，其权重也就越大。相反，某个指标的信息熵越大，表明指标值得变异程度越小，提供的信息量也越少，在综合评价中所起到的作用也越小，其权重也就越小。

你会发现在这段话中，自信息和提供信息实际上是成反比的。

不管他，只需要知道原本越稳定的数据，对异常越敏感，也越可信。

在实际计算中，遵循以下步骤：

step1 归一化

正向指标
$$Y_{ij}=\frac{X_{ij}-min(X_i)}{max(X_i)-min(X_i)}$$
负向指标
$$Y_{ij}=\frac{max(X_i)-X_{ij}}{max(X_i)-min(X_i)}$$
step2 求频率替换概率
$$p_{ij}=\frac{Y_{ij}}{\sum Y_{ij}}$$
step3 计算归一化信息熵
$$Entropy=-\frac{1}{ln(n)}\sum p_{ij}ln(p_{ij})$$
以什么为底的不重要啦

step4 计算权重
$$W_j=\frac{1-E_j}{k-\sum E_j}$$

---

以下是实现代码：

def EWM(data):
    t=(data-data.min(axis=0))/(data.max(axis=0)-data.min(axis=0))
    t=t/t.sum(axis=0)
    t[t<0.0001]=0.0001
    entropy=-1/np.log(t.shape[0])*np.sum(t*np.log(t))
    return [(1-i)/(len(entropy)-sum(entropy)) for i in entropy]

当然，这样的结果只是个权重，我们还需要对数据做乘法：

np.matmul(data.values,np.array(EWM(data)).T)

对这样一组数据，A十分稳定，B是正态分布，C是二分布，得到的结果是：

信息熵：

权重：

---

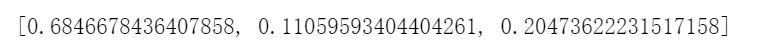
确实符合越稳定权重越大。

熵权法的优点

熵值法是根据各项指标指标值的变异程度来确定指标权数的，这是一种客观赋权法，避免了人为因素带来的偏差。

相对那些主观赋值法，精度较高客观性更强，能够更好的解释所得到的结果。

熵权法的缺点

忽略了指标本身重要程度，有时确定的指标权数会与预期的结果相差甚远，同时熵值法不能减少评价指标的维数，也就是熵权法符合数学规律具有严格的数学意义，但往往会忽视决策者主观的意图；

如果指标值的变动很小或者很突然地变大变小，熵权法用起来有局限