目录
编辑
一,问题描述
1.例子:
题目接口:
二,问题分析和解决
1.问题分析
2.解题代码
一,问题描述
首先我们得来先看看全排列的问题描述。全排列问题的问题描述如下:
给定一个不含重复数字的数组
nums,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
1.例子:

题目接口:
class Solution {
public:
vector<vector<int>> permute(vector<int>& nums) {
}
};二,问题分析和解决
1.问题分析
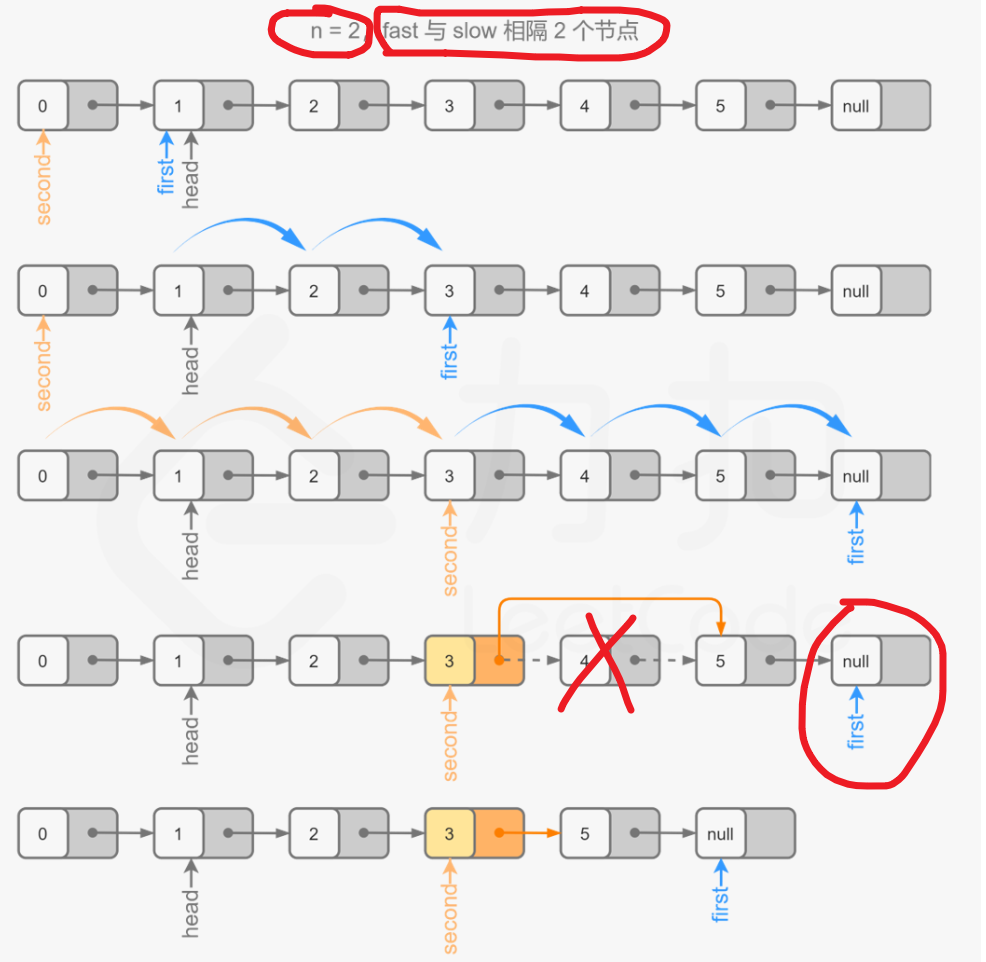
在上面的例子中我们可以看出全排列的问题就是在给出一个数组以后,找出这个数组中的数字的不同组合。这个组合的数字个数和数组的数字个数相同。如下图,我们给出:1,2,3的例子。我们可以画出下图:
在这个树中被红线划掉的路径就是被剪掉的路径。这个操作就叫作剪枝。在匹配完一对数据以后回到上一层树枝继续匹配的操作叫做回溯,在这棵树中的结束条件便是在将一棵树的一个路径遍历完了。
2.解题代码
class Solution {
public:
//全局变量:
vector<vector<int>> ret;
vector<int>path;
vector<vector<int>> permute(vector<int>& nums) {
vector<bool>used(nums.size(),false);//标记使用过的数字。
dfs(nums,used);
return ret;
}
void dfs(vector<int>&nums,vector<bool>&used)
{
if(path.size() == nums.size())//递归出口
{
ret.push_back(path);
return;
}
for(int i = 0;i<nums.size();i++)
{
if(used[i])//剪枝操作,当该节点已经用过以后便不能再插入到path中。
{
continue;
}
path.push_back(nums[i]);
used[i] = true;
dfs(nums,used);
//当程序程序执行到这里时便是返回到了上一层,也就是发生了回溯。在这里就要将下一次做的事情给纠正过来。
path.pop_back();
used[i] = false;
}
}
};在这段代码中,首先映入眼帘的便是两个全局变量ret和path。为什么要用全局变量呢?因为全局变量的引入可以让我们的递归函数传参变得简单,并且可以将回溯后的调整展示出来。否则,这个递归代码将会变得不好书写。










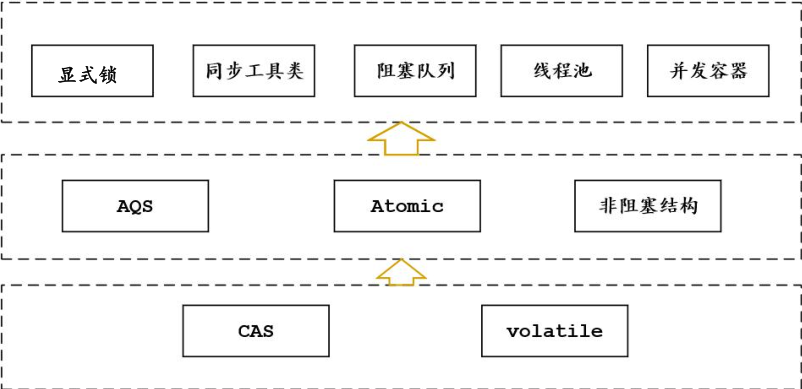


![java八股文面试[多线程]——并发三大特性 原子 可见 顺序](https://img-blog.csdnimg.cn/36c3a2a28bd74d2aa98429af4793c1ac.png)