全文链接:https://tecdat.cn/?p=33499
响应面(Response Surface Methodology,RSM)分析是一种常用的统计方法,用于研究和优化生产过程中的影响因素。通过建立数学模型来描述因素与响应之间的关系,RSM可以帮助我们识别并优化影响因素的设置,以达到最佳的生产结果(点击文末“阅读原文”获取完整代码数据)。
相关视频
在本研究中,我们将帮助客户应用R语言中的响应面分析技术来探索和优化生产过程中的关键影响因素。通过收集实验数据并建立合适的数学模型,我们将评估各个因素对于生产过程的影响,并通过优化因素水平来达到最佳的生产效果。同时,我们将针对交互作用效应进行进一步的分析,以深入理解影响因素之间的相互作用对生产结果的影响。
通过这项研究,我们期望为生产过程的优化和改进提供有价值的信息和指导。通过响应面分析方法,我们可以更好地理解和管理生产过程中的关键影响因素,并为提高生产效率、降低成本和提升产品质量做出贡献。
1、响应面分析与优化设计
试验设计与优化方法,都未能给出直观的图形,因而也不能凭直觉观察其最优化点,虽然能找出最优值,但难以直观地判别优化区域。为此响应面分析法(也称响应曲面法)应运而生。响应面分析也是一种最优化方法,它是将体系的响应作为一个或多个因素的函数,运用图形技术将这种函数关系显示出来,以供我们凭借直觉的观察来选择试验设计中的最优化条件.
显然,要构造这样的响应面并进行分析以确定最优条件或寻找最优区域,首先必须通过大量的测试验数据建立一个合适的数学模型(建模),然后再用此数学模型作图。那么我们来看看响应面分析的主要建模方法。
2、响应面建模数学方法
根据响应逼近函数形式的不同,响应面建模方法主要分为多项式回归法、神经网络法、Kriging函数法和径向基函数法等,各种方法都有一定的局限性。
实例
我们将要使用的一个实例就是:工程师有兴趣在确定在哪些条件下运作的生产过程是最大化。这两个变量可以控制的影响的生产过程:在反应时间(x1)和反应温度(x2)。工程师目前的操作条件是反应时间 35 分钟,温度 155ºF,生产率为 40%。这不可能是最佳区域,因此她拟合了一个一阶模型。
首先,拟合了一个一阶模型,以检验响应变量与温度和时间因素之间的真实函数是否接近于线性函数。
设立一个模型的回应曲面
首先收集并分析 B1 区块的数据,然后添加 B2 区块并进行新的分析。在大多数情况下,可以通过对 k 个自变量的水平进行编码来简化参数估计的计算。为了创建一个编码数据集,我们将使用以下公式:
Chemact, x1 ~(Time - 85)/5, x2 ~(Temp - 175)/5)
CR[1:7,]
coded.data(转换预测值并用编码版本替换这些变量) 在第一阶段,使用以下命令拟合一阶模型:
rsm(Yield~FO(x1,x2),data =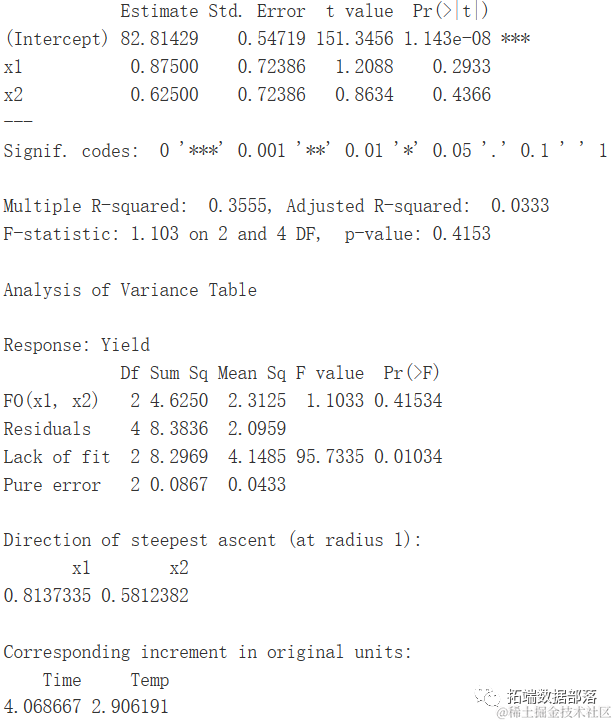
由于拟合度明显不足(p 值 = 0.01),因此应使用高阶模型。拟合模型没有任何特征允许我们估计响应变量的值。由于模型拟合中没有二次项或交互项,变量 x1 和 x2 不显著。因此,交互项被包含在内:
CR.rsm1.5 <- update(
summary(CR.rsm1.5)

同样,在这种情况下,拟合度的缺失是显著的,p 值 = 0.005。为了建立二阶模型,我们加入了模块 2 的数据。这可以使用 "SO(x1,x2) "来完成,其中包括二次项和交互项:
CR. Yield ~ Block + SO(x1, x2
summary(CR.rsm2)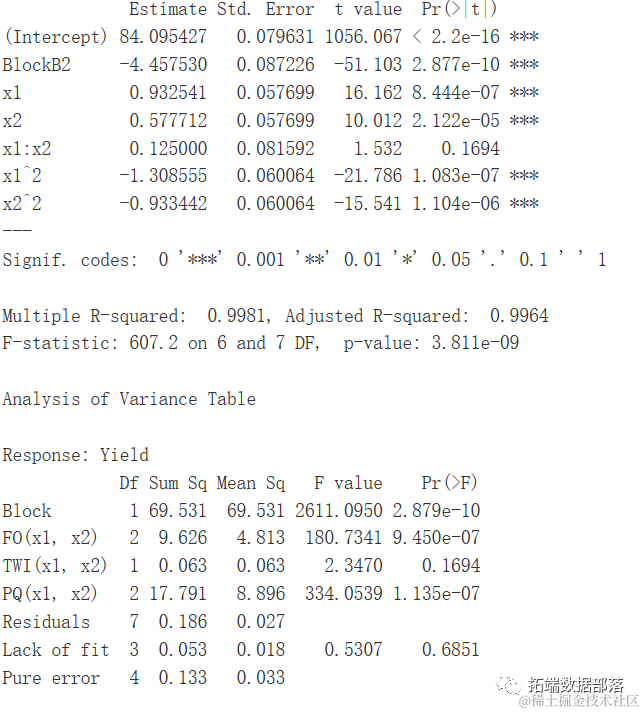
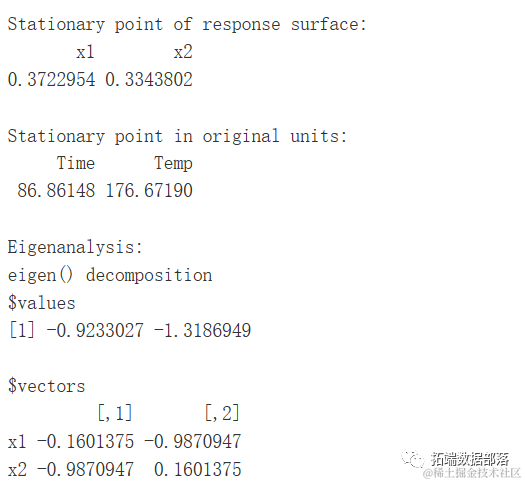
现在,拟合不显著(p 值 = 0.69),即二阶模型很好地拟合了数据。还可以看出,拟合模型的静止点位于(0.37; 0.33),即最大值点。
可以使用 lm 函数(线性模型)或 rsm 函数(响应面方法)来构建水平曲线和响应面。
fit.model <- rs me,Temp))
contour(fit.model, " col = inbw(40))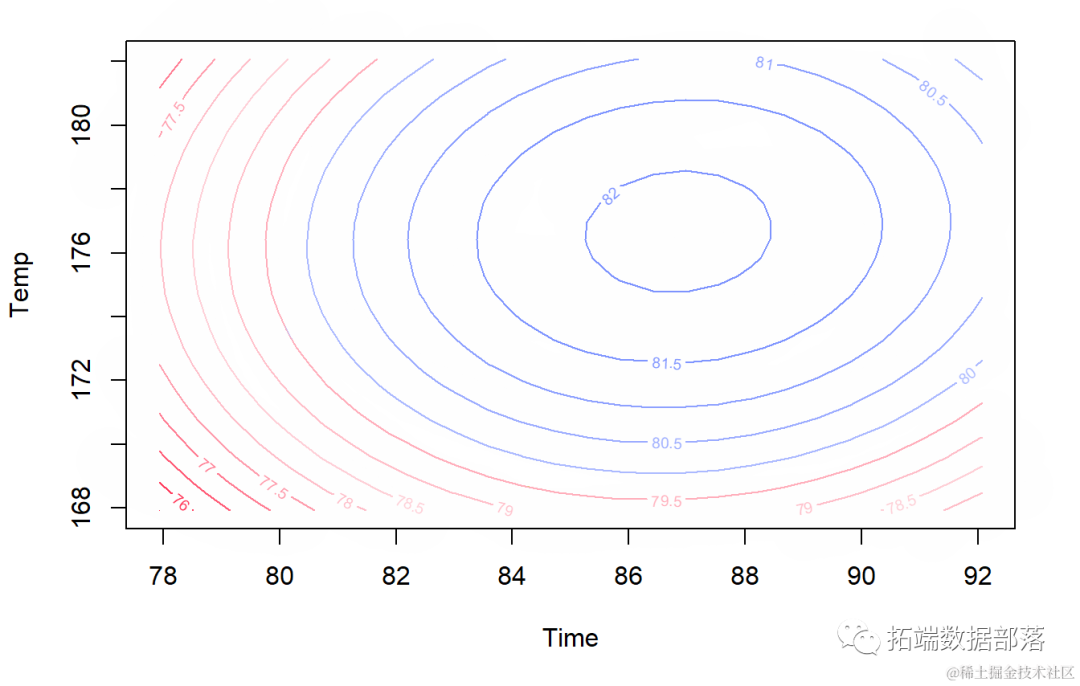
点击标题查阅往期内容

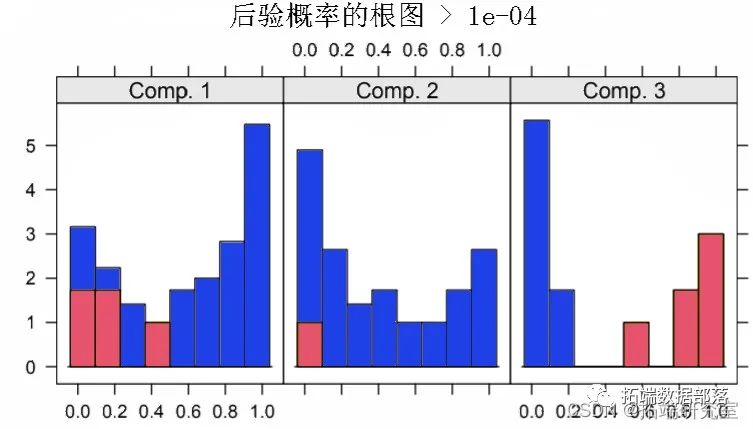
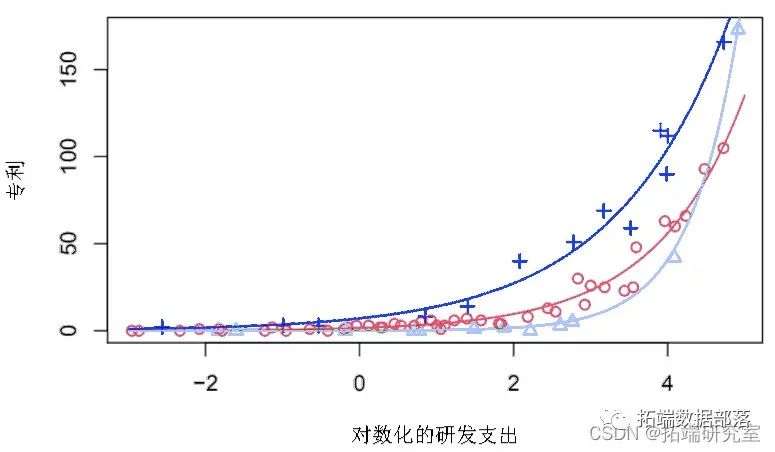
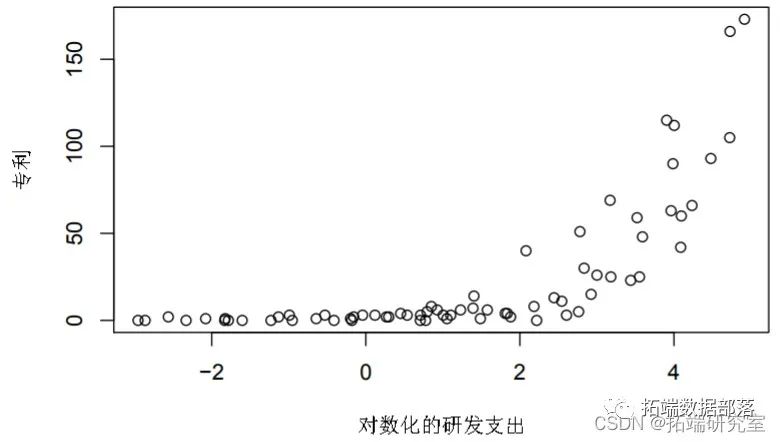
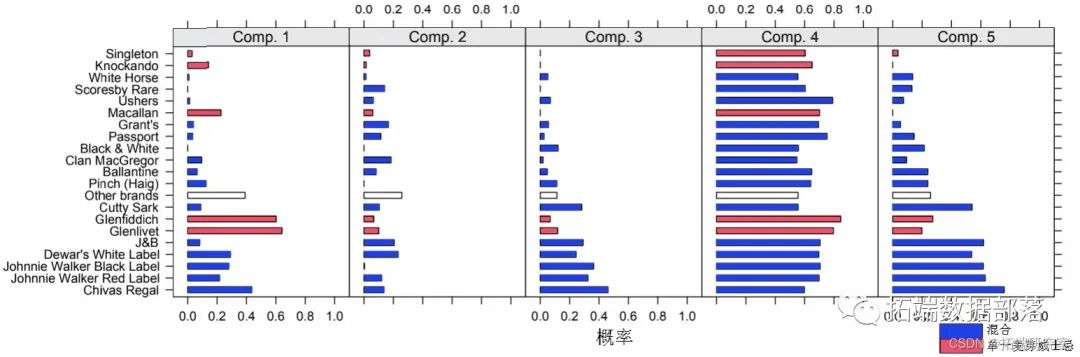
有限混合模型聚类FMM、广义线性回归模型GLM混合应用分析威士忌市场和研究专利申请数据

左右滑动查看更多

01
02
03
04
可以看出,当 x1(时间)的值接近 85 分钟和 x2(温度)的值接近 175ºF 时,响应变量的值达到最大。如上所述,我们可以更精确地找到方差分析得出的静止点,即 x1 = 86.86148 和 x2 = 176.67190。
最后是响应面图:
psp(fitodel,~Time+Temp)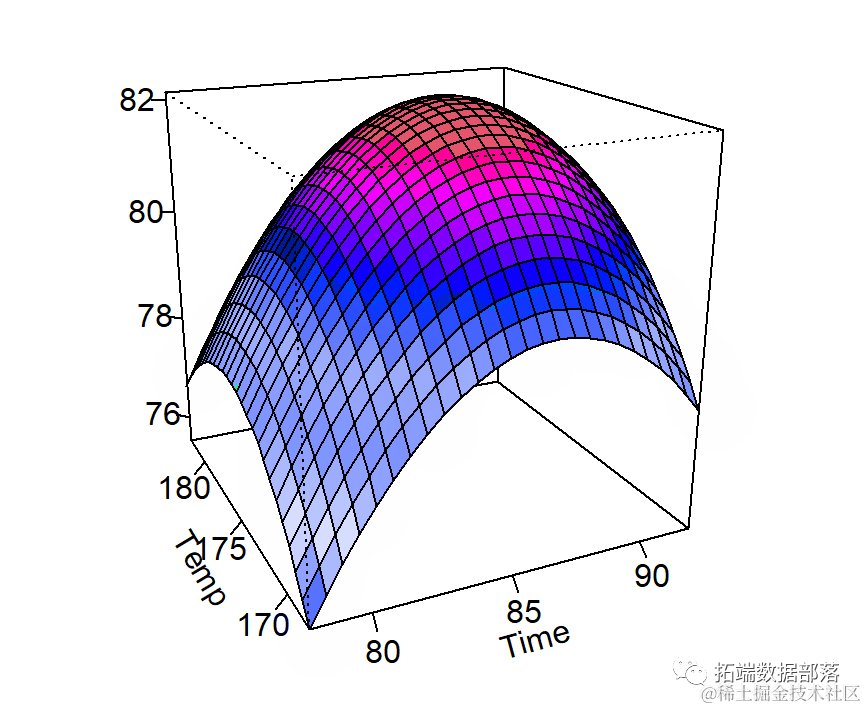

点击文末“阅读原文”
获取全文完整代码数据资料。
本文选自《R语言响应面(RSM)、线性模型lm分析生产过程影响因素可视化》。


点击标题查阅往期内容
数据分享|R语言逻辑回归、线性判别分析LDA、GAM、MARS、KNN、QDA、决策树、随机森林、SVM分类葡萄酒交叉验证ROC
Python用PyMC贝叶斯GLM广义线性模型、NUTS采样器拟合、后验分布可视化
数据分享|用加性多元线性回归、随机森林、弹性网络模型预测鲍鱼年龄和可视化
R语言高维数据惩罚回归方法:主成分回归PCR、岭回归、lasso、弹性网络elastic net分析基因数据(含练习题)
Python中LARS和Lasso回归之最小角算法Lars分析波士顿住房数据实例
R语言Bootstrap的岭回归和自适应LASSO回归可视化
R语言Lasso回归模型变量选择和糖尿病发展预测模型
R语言实现贝叶斯分位数回归、lasso和自适应lasso贝叶斯分位数回归分析
基于R语言实现LASSO回归分析
R语言用LASSO,adaptive LASSO预测通货膨胀时间序列
R语言自适应LASSO 多项式回归、二元逻辑回归和岭回归应用分析
R语言惩罚logistic逻辑回归(LASSO,岭回归)高维变量选择的分类模型案例
Python中的Lasso回归之最小角算法LARS
r语言中对LASSO回归,Ridge岭回归和弹性网络Elastic Net模型实现
r语言中对LASSO回归,Ridge岭回归和Elastic Net模型实现
R语言实现LASSO回归——自己编写LASSO回归算法
R使用LASSO回归预测股票收益
python使用LASSO回归预测股票收益

![]()