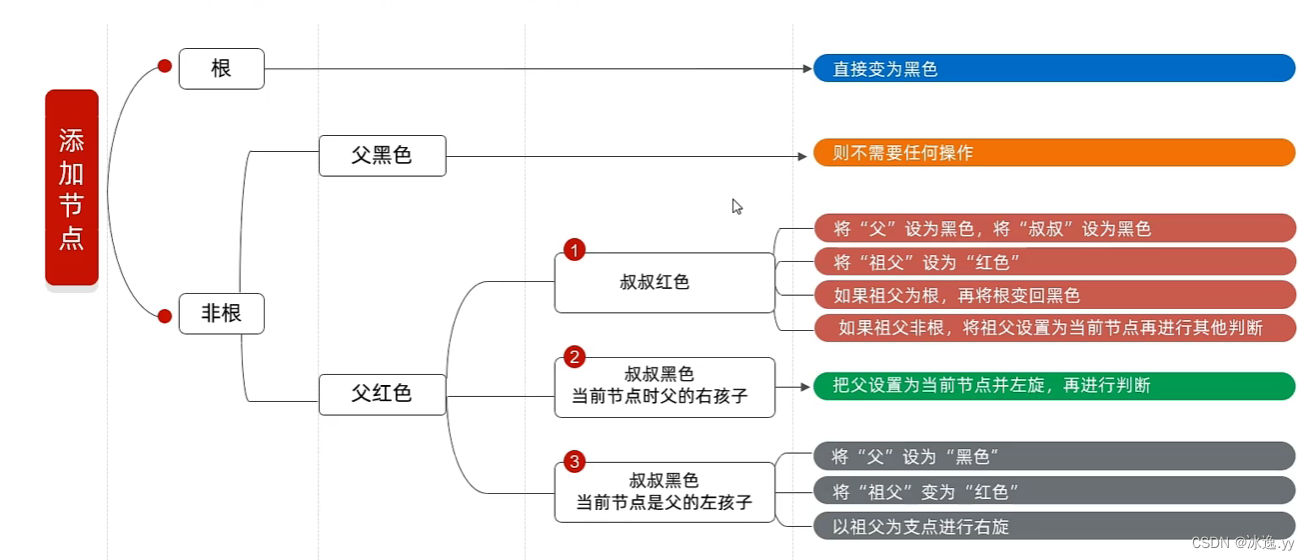
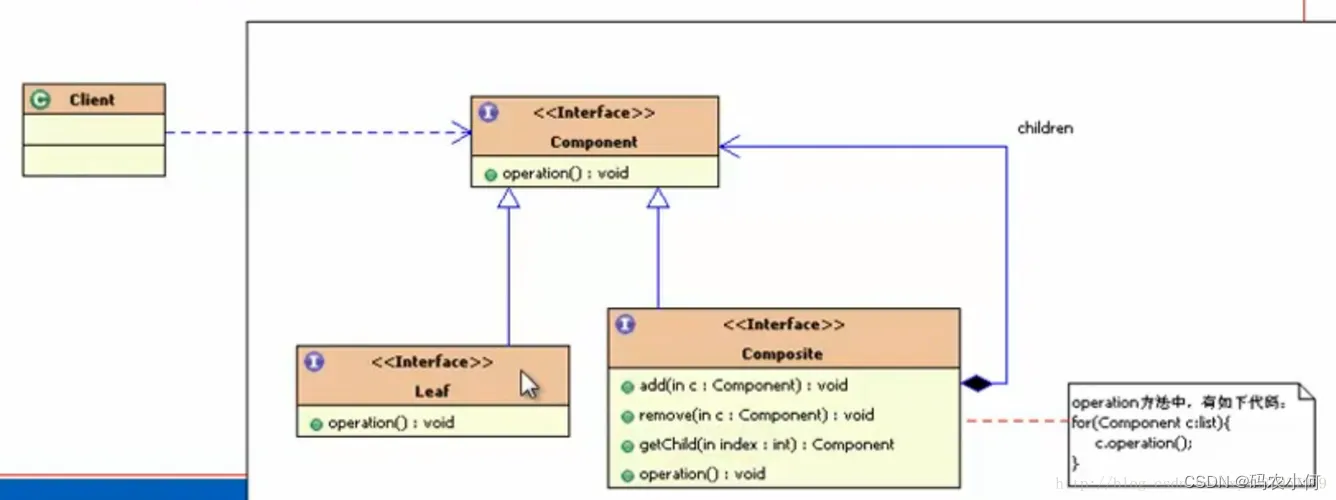
堆是将一组数据按照完全二叉树的存储顺序，将数据存储在一个一维数组中的结构。堆有两种结构，一种称为大顶堆，一种称为小顶堆，如下图。

• 小顶堆：任意节点的值均小于等于它的左右孩子，并且最小的值位于堆顶，即根节点处。

• 大顶堆：任意节点的值均大于等于它的左右孩子，并且最大的值位于堆顶，即根节点处。有些地方也叫大根堆、小根堆，或者最大堆、最小堆都一个意思。大和小的特征等都是类以的，只是比较的时候是按照大还是小来定，我们本章在原理方面的介绍就按照最大堆来进行，后面的题目再根据情况来定。

使用数组构建堆时，就是先按照层次将所有元素依次填入二叉树中，使其成为二叉树，然后再不断调整，最终使其符合堆结构。

下面就看一下如何建立一个大堆：

将元素依次排到完全二叉树节点上去，如下左图所示。 a. int i = (size - 2) / 2 = 4 (思考一下这里为什么是size-2而不是size-1)。找到数组中的4号下标。65大于其孩子，满足大堆性质，所以不用交换。如下右图

 

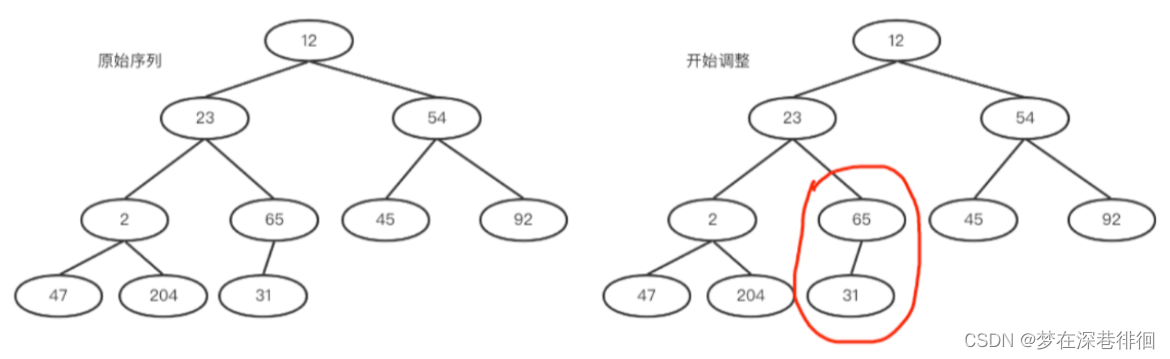
b. 然后 i = i - 1；然后用2和其孩子比较，2和204交换。交换之后204所在的子树满足大堆，如下左图。

c. 54和其孩子比较，54和92交换。此时92所在子树满足大堆，如下右图。

 

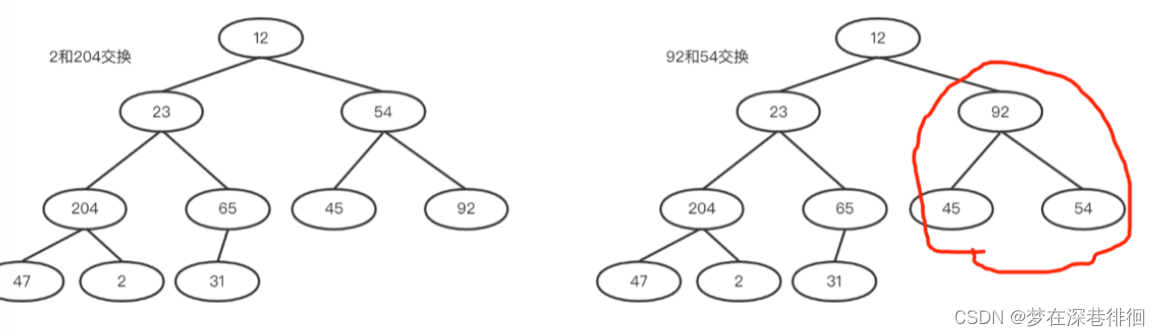
d. 继续，23和其孩子比较，23和204交换，交换完之后，23的子树却不满足了，所以还需调整它的子树。如下两图所示。

 

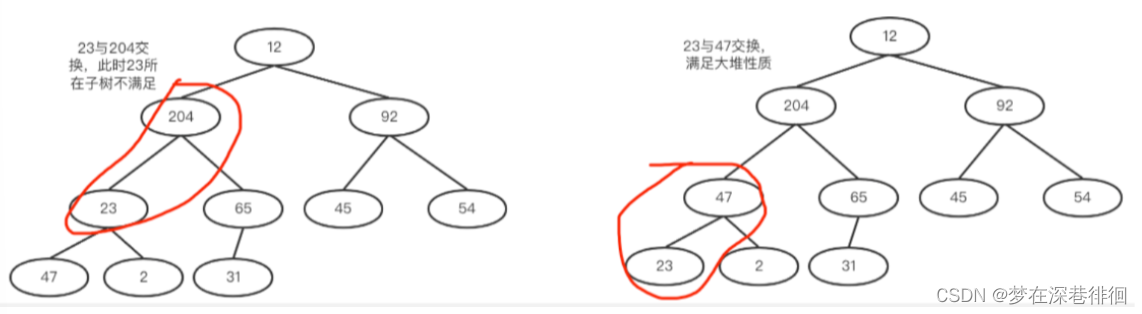
e. 12和204交换，仍然出现不平衡的情况，以比类推，直到根节点也满足要求就完毕了。

 

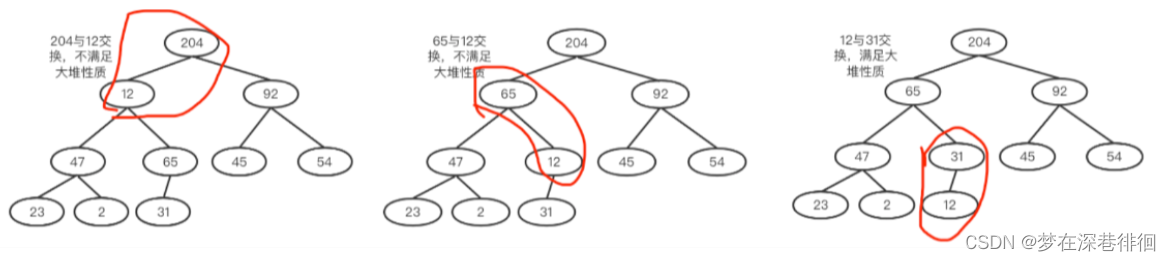
这样我们就建好了一个大顶堆。