今天为大家带来一期基于DBO-SVM的电力负荷预测。

原理详解

文章对支持向量机(SVM)的两个参数进行优化，分别是：惩罚系数c和 gamma。

其中，惩罚系数c表示对误差的宽容度。c越高，说明越不能容忍出现误差,容易过拟合。c越小，容易欠拟合。c过大或过小，泛化能力都会变差。

gamma是选择RBF函数作为kernel后，该函数自带的一个参数。隐含地决定了数据映射到新的特征空间后的分布，gamma越大，支持向量越少，gamma值越小，支持向量越多。支持向量的个数影响训练与预测的速度。

本文所选SVM是从官网下载的libsvm-3.3版本，作者已编译好，大家可以直接运行。如果想自行编译的童鞋可以从网站下载：https://www.csie.ntu.edu.tw/~cjlin/libsvm/index.html，编译步骤可以参考https://blog.csdn.net/qq_42457960/article/details/109275227

采用蜣螂优化SVM，参数设置范围分别是：

惩罚系数c	[0.001, 1000]
gamma	[2^-8,2^8]

将DBO种群数设置为：30，迭代次数设置为60。

---

数据准备

对电力负荷数据进行处理

本次数据包含负荷值，温度，湿度，风速，压强，降水量，能见度，水汽压和体感温度，部分数据截图如下：

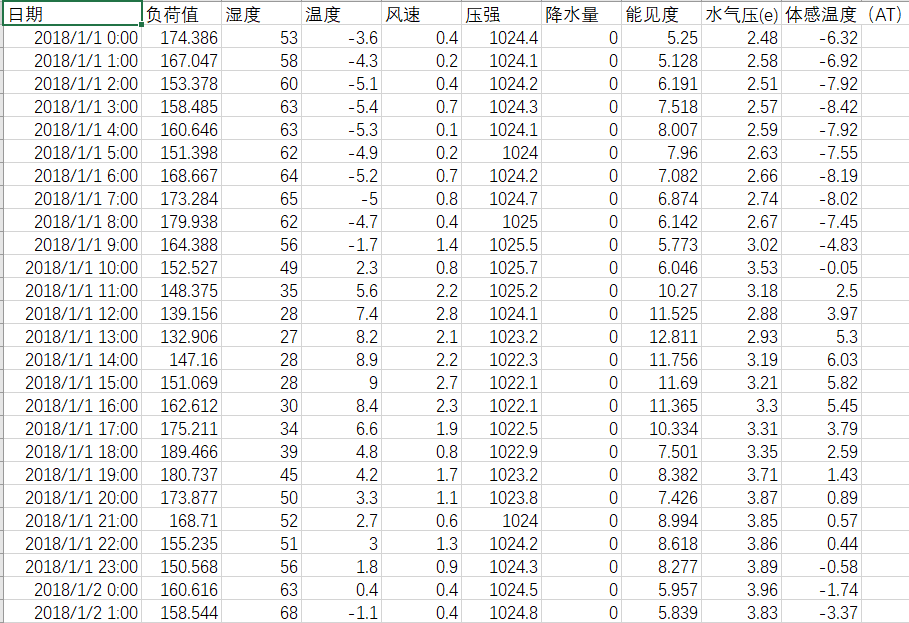
选取1200个样本作为训练集，每个样本组成为：当天24个小时的全部数据，因此训练集的输入数据大小为1200*216，其中216=24*9，24代表24个小时，9代表9个特征。训练集的输出数据大小为：1200*1。1代表未来一小时的负荷值。

选取100个样本作为测试集，同理，测试集的输入数据大小为100*216，训练集的输出数据大小为：100*1。

结果展示

采用SVM对电力负荷数据进行训练和预测

SVM的预测结果如下：

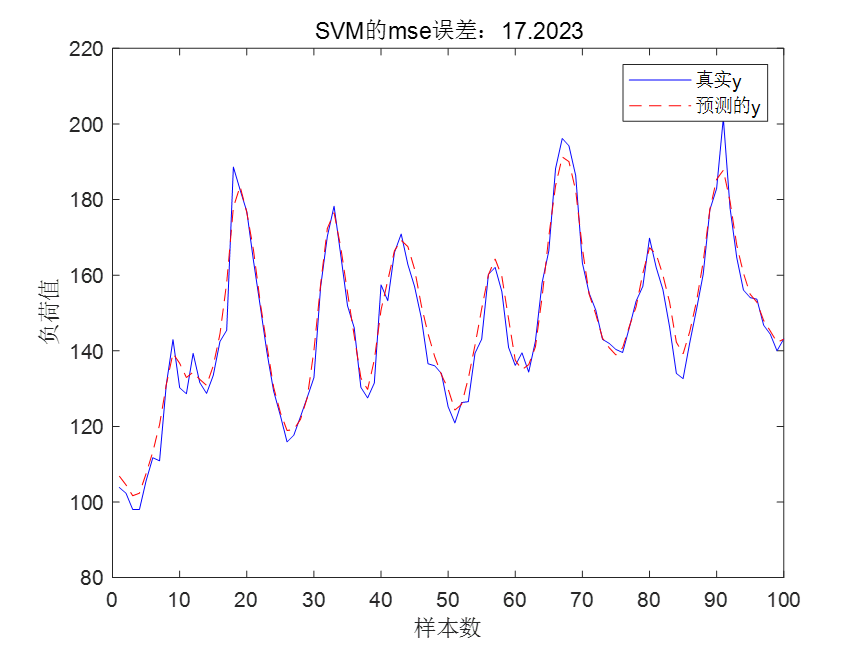
可以看到，未优化的SVM预测效果还是不错的，但是仍然有改进空间。

DBO-SVM模型的预测效果如下：

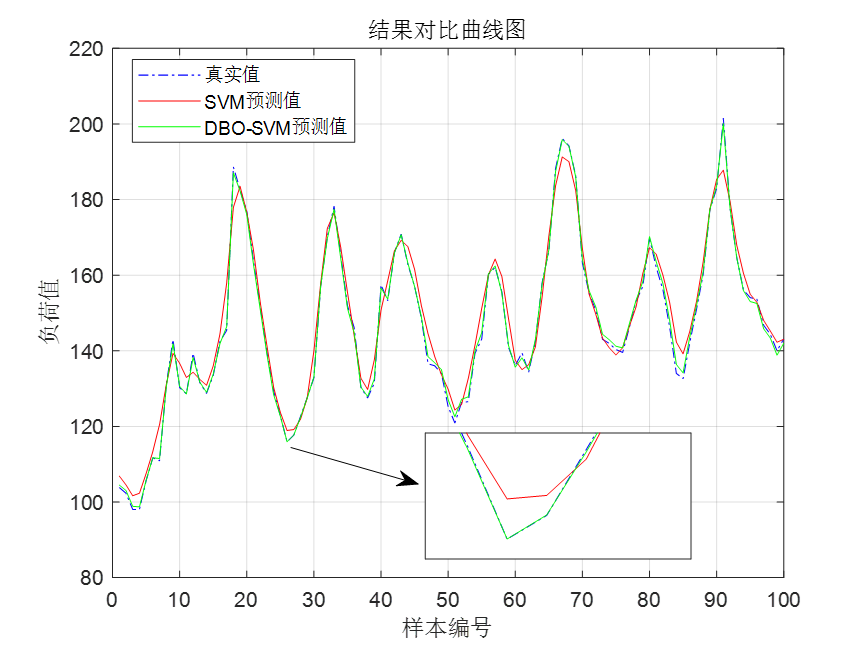
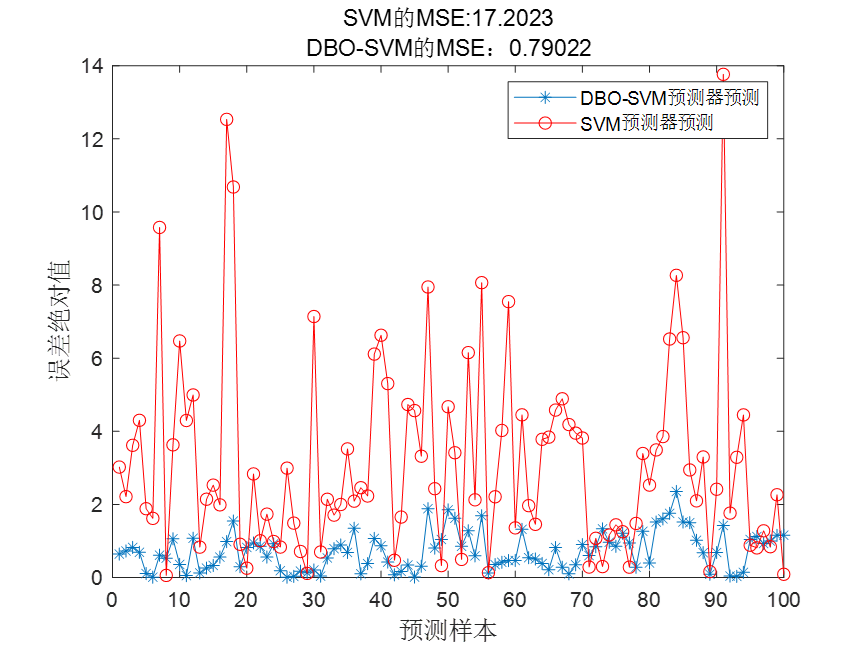
误差对比图如下：

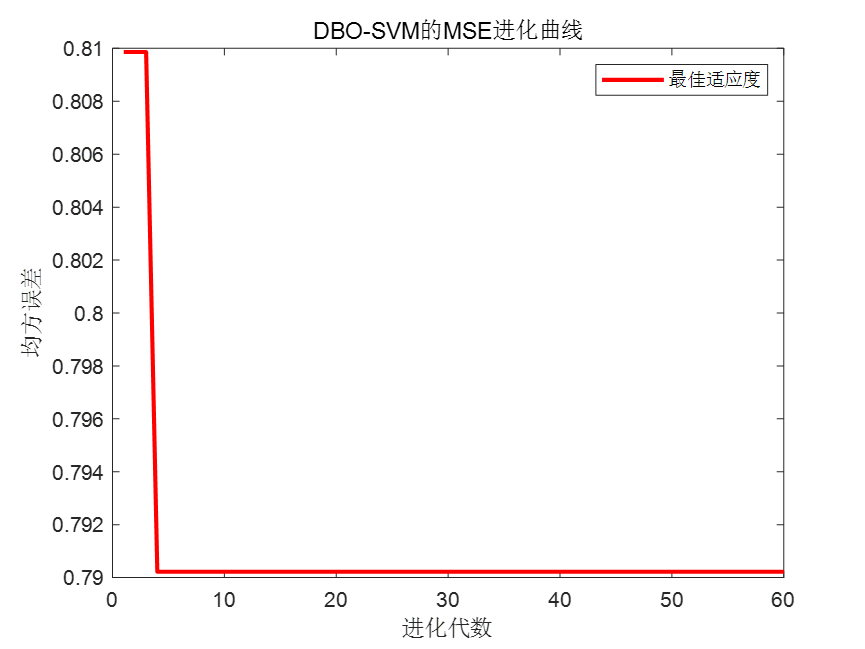
DBO-SVM的进化曲线：

可以看到DBO-SVM预测效果有了明显提升，DBO-SVM的MSE误差为0.79022，相比于未优化SVM的17.2023有了很大提升！

DBO-SVM的回归拟合图：

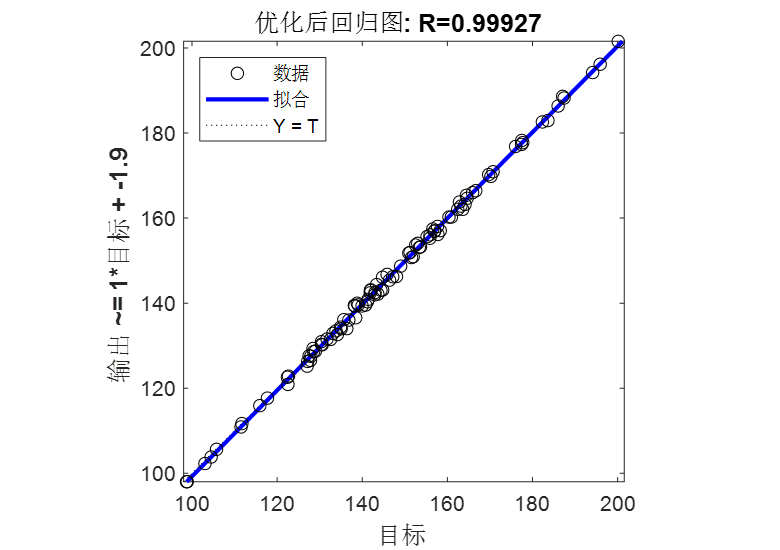
误差直方图：

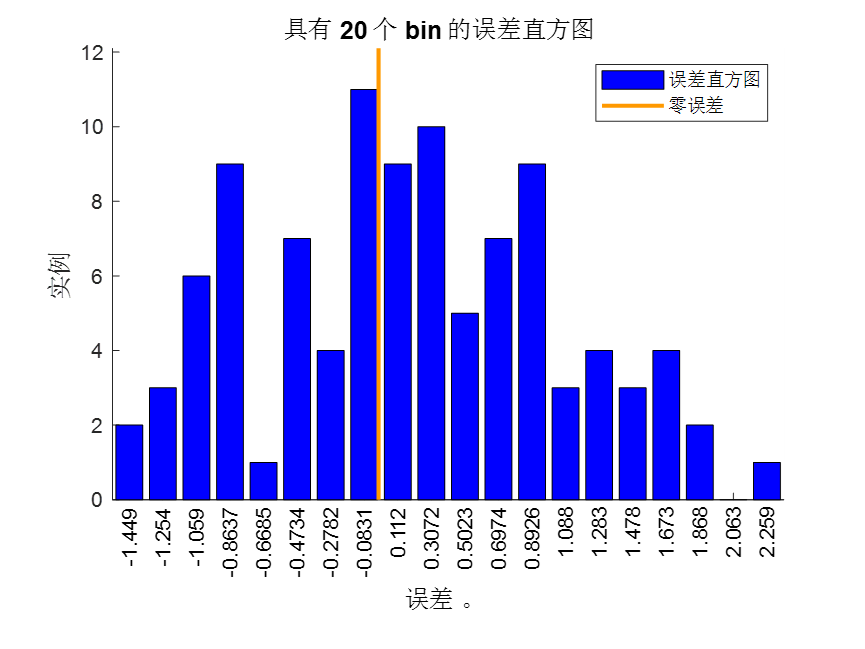
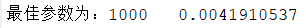
部分代码

%% 初始化DBO参数
pop=30;   %初始种群规模
maxgen=60;   %最大进化代数
lb = [10^-3, 2^-8];
ub = [10^3, 2^8];
dim = 2;
[fMin,bestX,Convergence_curve ] = DBOforSVM(pop, maxgen,lb,ub,dim,inputn,output_train,inputn_test,output_test);
bestc=bestX(1);
bestg=bestX(2);
disp(['最佳参数为：',num2str(bestX)])
cmd = [' -t 2',' -c ',num2str(bestc),' -g ',num2str(bestg),' -s 3 -h 0 -q'];
mode1= libsvmtrain(output_train,inputn,cmd);
[test_simu1,~,~]= libsvmpredict(output_test,inputn_test,mode1);
mse1=mse(output_test,test_simu1); 
error1 = output_test - test_simu1;


%% 绘制进化曲线
figure
plot(Convergence_curve,'r-','linewidth',2)
xlabel('进化代数')
ylabel('均方误差')
legend('最佳适应度')
title('DBO-SVM的MSE进化曲线')
% 绘制误差对比图
figure
plot(abs(error1),'-*')
hold on
plot(abs(error0),'-or')
title(['SVM的MSE:',num2str(mse0),newline,'DBO-SVM的MSE：',num2str(mse1)])
xlabel('预测样本','fontsize',12)
ylabel('误差绝对值','fontsize',12)
legend('DBO-SVM预测器预测','SVM预测器预测')
% 绘制结果对比曲线图
figure
plot(output_test,'b-.')
hold on
plot(test_simu0,'r')
hold on
plot(test_simu1,'g')
hold off
grid on
title(['结果对比曲线图'])
legend('真实值','SVM预测值','DBO-SVM预测值')
xlabel('样本编号')
ylabel('负荷值')


%% 回归图与误差直方图
figure;
plotregression(test_simu1,output_test,['优化后回归图']);
set(gcf,'color','w')


figure;
ploterrhist(test_simu1-output_test,['误差直方图']);
set(gcf,'color','w')


%% 打印出评价指标
% 预测结果评价
ae= abs(test_simu1-output_test);
rmse = (mean(ae.^2)).^0.5;
mse = mean(ae.^2);
mae = mean(ae);
mape = mean(ae./test_simu1);
[R,r] = corr(output_test,test_simu1);
R2 = 1 - norm(output_test -  test_simu1)^2 / norm(output_test-mean(output_test ))^2;
disp('预测结果评价指标：')
disp(['RMSE = ', num2str(rmse)])
disp(['MSE  = ', num2str(mse)])
disp(['MAE  = ', num2str(mae)])
disp(['MAPE = ', num2str(mape)])
disp(['决定系数R^2为：',num2str(R2)])

---

代码获取

完整代码获取，后台回复关键词：

DBOSVM