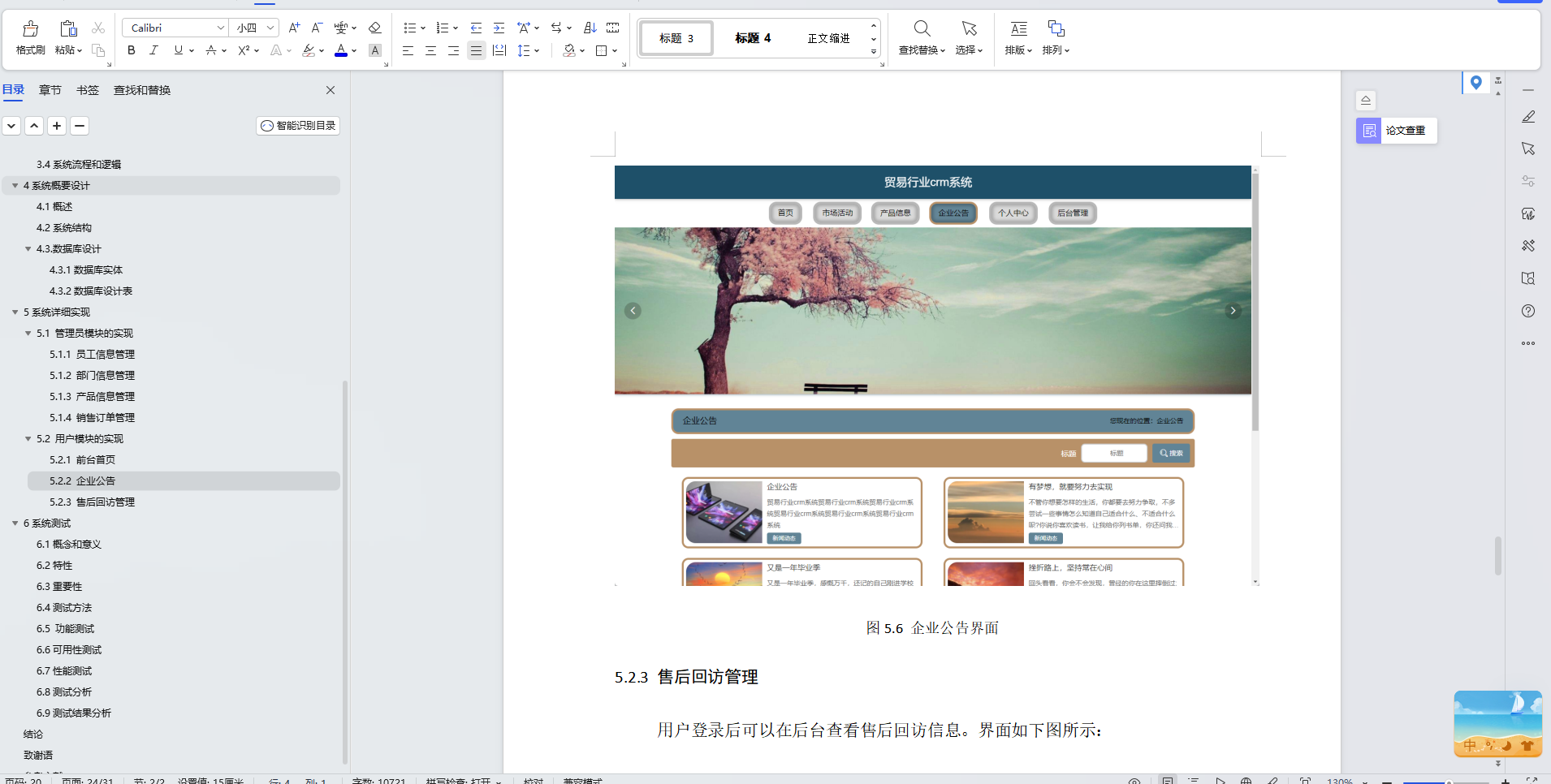
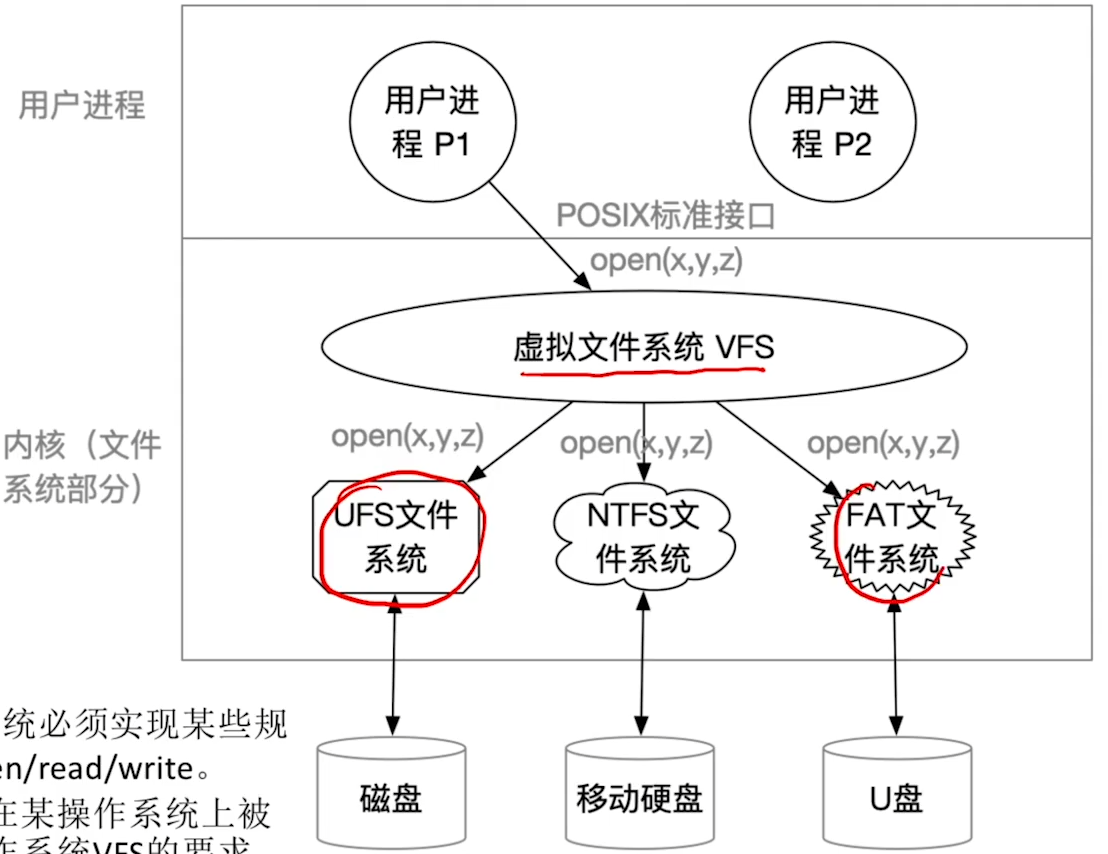
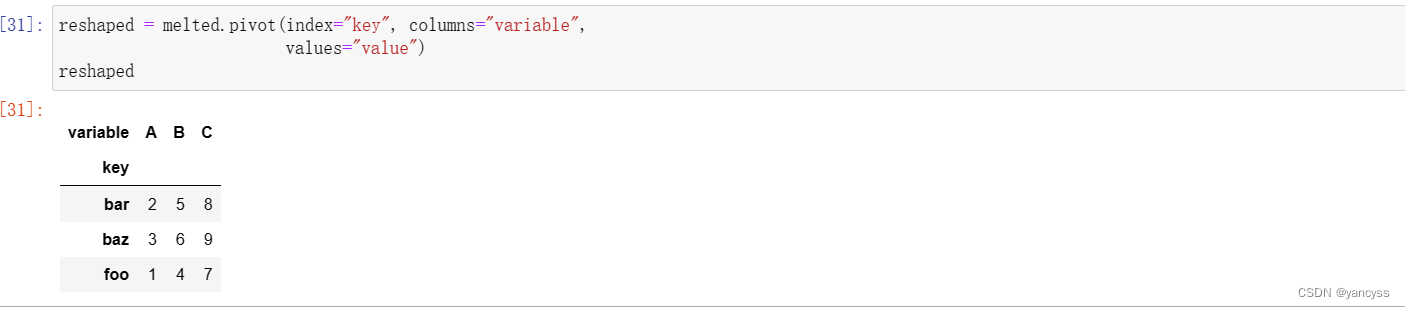
目录
简介
实现
代码
关于Floyd的题目
简介
首先我们要知道a到b的最短路是什么
a到b的最短路是从a点到b点的最小距离(花费)
那多源最短路呢就是能求任意a和b,之间的最短路
那么Folyd是多源最短路,也就是求任意a和b,之间的最短路
实现
首先介绍一种术语“松弛”
松弛的意思么就是这个点的最短路被更新,可以被一个点更新,也可以被b连着的变更新(dijkstra和bellman-ford和spfa)
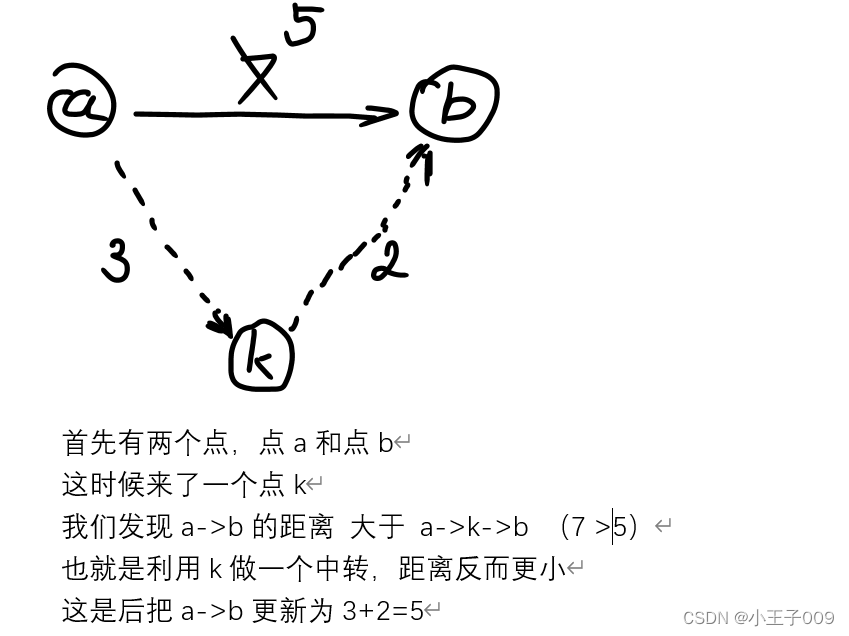
那么Floyd的思路是什么呢
- 选一个k
- 选一个a
- 选一个b
- 松弛 a->b
欸对了,有的小伙伴猜到了,三重循环!!! 简单吧
好到这里你应该知道代码怎么写了吧
还不会的小伙伴跟我来
代码
#include <iostream>
#include <cstring>
using namespace std;
const int N = 5e2 + 5;
int n, m;
int G[N][N]; //邻接矩阵
void Floyd() {
for (int k = 1; k <= n; k ++)
for (int a = 1; a <= n; a ++)
for (int b = 1; b <= n; b ++)
G[a][b] = min(G[a][b], G[a][k] + G[k][b]);
}
int main() {
cin >> n >> m;
memset(G, 0x3f, sizeof G);
for (int i = 1; i <= m; i ++) {
int a, b, c;
cin >> a >> b >> c;
G[a][b] = c; // a到b 距离为c
}
for (int i = 1; i <= n; i ++)
G[i][i] = 0;//自己到自己为0
Floyd();
// for (int i = 1; i <= n; i ++) {
// for (int j = 1; j <= n; j ++)
// cout << G[i][j] << ' ';
// cout << '\n';
// }
int a, b;
cin >> a >> b;
cout << G[a][b];
return 0;
}关于Floyd的题目
一本通1342
洛谷 模板


![5G+智慧交通行业解决方案[46页PPT]](https://img-blog.csdnimg.cn/img_convert/575618c3bf837a8e0090f59c3d1dbb10.jpeg)