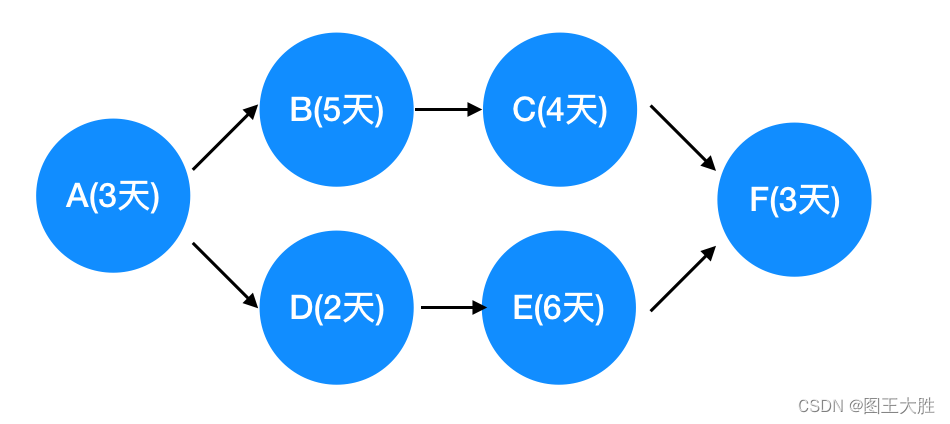
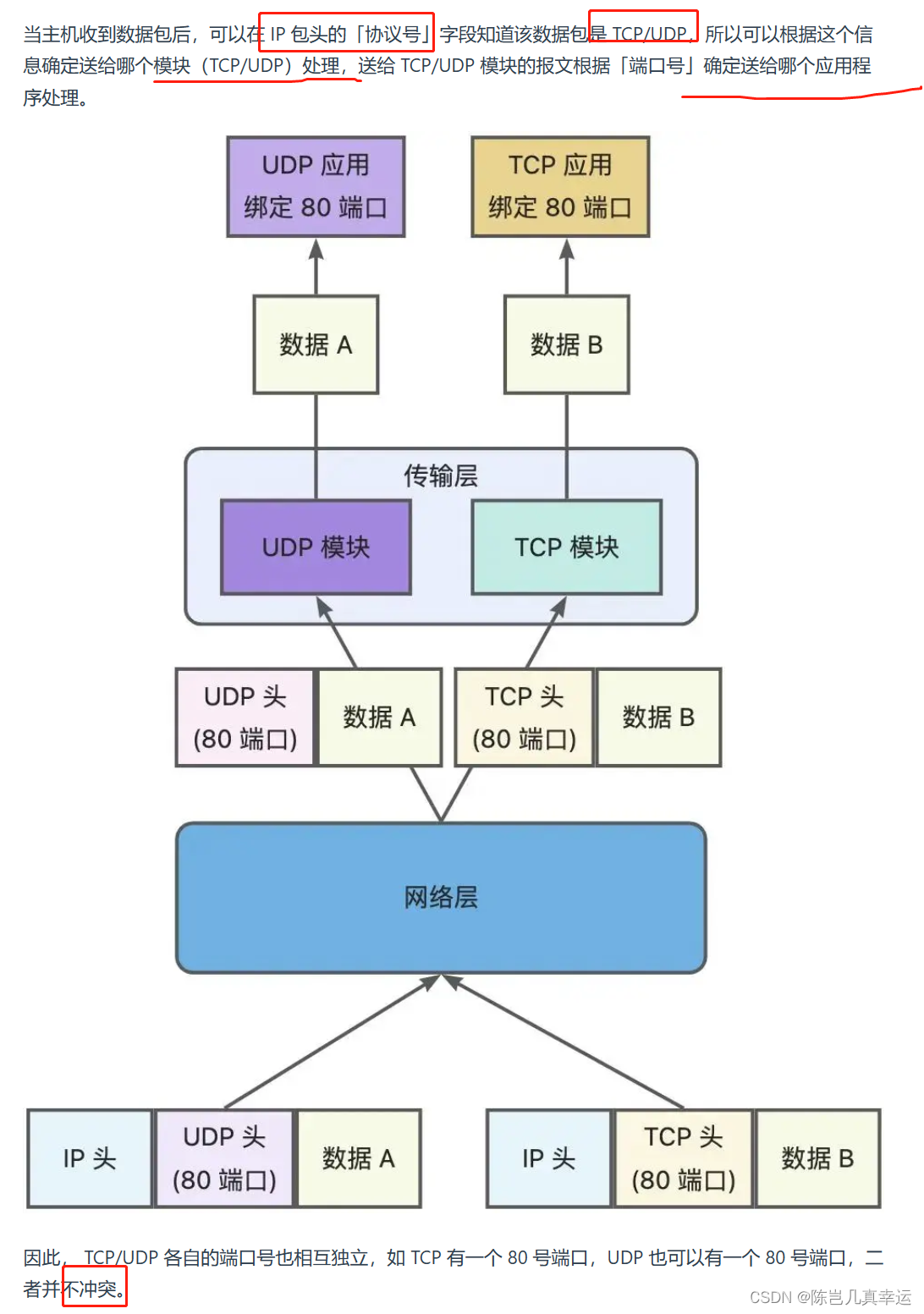
一、Distance field soft shadows

Inigo Quilez :: computer graphics, mathematics, shaders, fractals, demoscene and more (iquilezles.org)

在开始我们的实时环境光照之前，我们再说一种现在的实现实时软阴影的方式，也就是Distance field soft shadows，也就是距离场软阴影，它的效果图如上图。

1.距离场回顾

c - Signed distance field calculation bug - Stack Overflow

关于距离场/距离函数我们在GAMES101的几何章节中提到过，它定义了空间中每一个点到某一物体表面的最小距离。它可以有正负号，代表该点在物体的内部还是外部，这样一来它就不仅定义了距离，而是定义了有向距离，所以我们一般简称为SDF。上图所示为字母A的SDF的可视化图。

在GAMES101里我们提到过这个例子，假设上图中的黑色是某一物体，A时刻在一个位置，而在B时刻移动到了另外一个位置，我们想得到它的边界是如何运动的，如果只用lerp线性插值只能得到全灰色的一条过渡带，如上图。而如果我们先把A和B时刻物体的SDF求出来（图中蓝色表示在物体内，所以SDF<0），然后再对A和B的SDF进行lerp线性插值就可以恢复出来物体的边界和运动过程。

SDF还有一个比较好的用处，就是可以得到任意两个几何的blending，而不需要关心这两个几何之间的拓扑关系。如上图球形靠近正方形融合的过程就是使用了SDF进行blend，由此可见SDF可以得到一个非常好的过度。SDF背后的理论为Optimal Transport，也就是最优传输，有兴趣的朋友可以自行学习，这里就不提了。

2.光线步进—Ray marching

Mesh Distance Fields in Unreal Engine | Unreal Engine 5.2 Documentation

SDF另一个很好的用处是Ray Marching也就是光线步进，这里在GAMES101里并没有提到，它实际上也就是一种光线追踪。由于我们定义了SDF，那么我们就知道场景空间中每个点到场景每个物体表面的最短距离，我们就可以用一个球表示当前光线步进的安全距离（该距离为各个SDF中最小的距离），因为SDF告诉我们在这个球的范围中，我们步进半径的距离是不会穿过任何物体的，如上图所示。最后，不断步进直到与物体表面距离足够小或者追踪足够远了仍然没打到任何物体停下来，这就是Ray Marching。

3.SDF生成软阴影

接下来我们分析如何利用SDF生成软阴影，也就是Distance field soft shadows，在上面说Ray Marching的时候，我们提到了SDF为我们的光线步进提供了一个安全距离的参考，使得我们不会步进步长过大。而SDF在生成软阴影中则为我们提供了一个安全角度，如上图所示。从上图我们可以观察到，当我们从一个着色点出发向一个光源，其中在这条线上通过SDF可以为我们提供一个安全角，取决于这条线上最短的SDF，而显然安全角越小，这个点被挡住的光就越多，自然也就越黑。

那么这个安全角如何计算呢？光线步进的距离我们知道了，这也就是三角形的斜边，然后SDF的距离那也就是直角边，这样只需要计算arc sinθ就可以了，但实际上人们很少做这种复杂的计算。

如上图，正常的计算公式是左边的 $arcsin\frac{SDF(p)}{\left | p-o \right |}$ ,而事实上人们用的是右面的公式 $min\left \{ \frac{k\cdot SDF(p)}{\left | p-o \right |} ,1.0\right \}$ ,因为这个公式就已经能判断阴影的大小了，反三角的计算又很复杂，所以没必要算的那么精确，直接乘以一个常数k代替arcsin即可，最后为了保证visibility不能超过1，再做一个min截断即可。至于k在一定程度上决定了半影区过度的速度或者说软硬程度，如果k特别大，得出的阴影自然和硬阴影一样。(例如k取100，则过渡带为0~0.01，非常小)

SDF可视化：Mesh Distance Fields in Unreal Engine | Unreal Engine 5.2 Documentation

4.Distance field soft shadows的问题

(1)优点

1.快*，相比Shadow map不考虑预计算花费的时间，查找SDF比Shadow map的遍历纹理快。

2.高质量

(2)缺点

1.场景的SDF需要预计算

2.存储SDF需要大量的空间

3.如果有物体发生形变，需要重新计算SDF

5.SDF的存储

我们提到SDF是一个三维空间的数据，相当于我们要存储一个三维的纹理，这么大的数据量我们怎么存储呢？事实上，人们经常用我们之前GAMES101提到的空间数据结构来存储SDF，包括KD树，八叉树等等来划分空间，然后划分的某些区域可能离场景中绝大多数物体很远，那我们自然就没必要去把它划分的那么精细，可以直接用一个大的节点来记录。划分直到在一个节点内，它的SDF变化非常剧烈的情况下，就精细的划分记录在叶子节点上。

二、环境光照的着色—Shading from environment lighting

1.Image-Based Lighting (IBL)

在GAMES101里我们提到过环境光照的解决方法，就是把环境光记录在一张图上，是球也好或者是Cubemap也好（默认环境光来自无限远），都属于基于图像的光照，也就是IBL。那么给定了我们环境光照，我们如何对任意一个着色点(不考虑阴影遮挡)计算它的环境光着色呢？

计算环境光着色，我们自然想到去解渲染方程。实时渲染中我们经常把Visibility项拆出来，而又因为我们现在不考虑Visibility，所以现在只剩下了来自四面八方的环境光照Li，又因为要考虑法线方向的正半球积分，所以要么积分域为Ω+。

那么如何解这个积分呢，在GAMES101中我们提到可以用蒙特卡洛积分法来解渲染方程，但显然这是非常非常慢的，因为涉及到大量的采样。

那么我们有没有不采样的方法呢？

2.Prefiltering

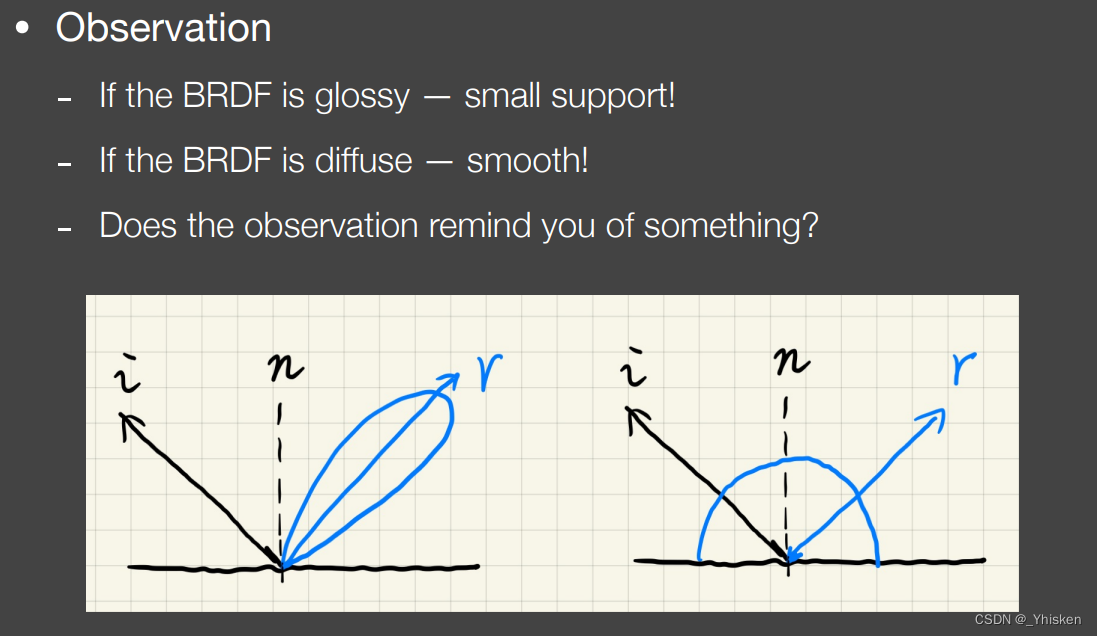
这里有一个很有趣的观察，我们知道前面我们的渲染方程形式是对Li和BRDF的乘积做了一个积分，在前面我们提到过一个约等式可以把乘积的积分改为积分的乘积，但是有两个条件，一个是要么其中一个函数的积分线较小，要么比较smooth。而通过观察我们发现，Glossy的BRDF正好是积分域比较小，而Diffuse的BRDF正好足够smooth，这样就正好满足我们约等式准确的条件。

如上图，我们通过约等式就可以把Light项拆出来，(在当时计算阴影的时候我们拆的是Visibility项)。所以这个约等式是可以根据不同情况把不同项当成g(x)的。

那么拆出来这一项，也就是黄色方框里的项是在干嘛呢？可以看到对区域做积分之后又除了一个积分，显然是归一化，这就相当于给平均了，而又是一定范围内的平均，那显然就是“模糊”操作。这里我们把它叫做Prefiltering，我可以滤波环境光，至于滤波核取多大，自然就取决于BRDF占多大。Pre体现在哪里呢？这里是在进行渲染之前就已经把这些图做好模糊了，已经预生成好了，所以叫Prefiltering。至于不同大小滤波核模糊的结果的查询，可以参考Mipmap，用层与层之间的三线性插值即可。