一、向量(Vector)
点乘(Dot Product)
- 定义:计算两个单位向量的夹角
- 用途:
- 描述两个向量是否足够接近
叉乘(Cross Product)
- 定义:用于判断法向量的防线,一般遵循右手螺旋定则,手指指向方向和叉乘向量的顺序相反
- 用途:
- 判断叉乘两个向量的左右方向,如a叉乘b与正交坐标系的y轴同向,则a在b的左边
- 判断点与三角形的位置关系(点P与三角形三个顶点连接的向量相乘,如果结果方向均一致,说明P在三角形内,反之则外)
二、变换(Transform)
- 变换都基于坐标轴原点来操作
- 图形图像的变化可以简化成矩阵加减/相乘的形式进行计算
- 线性变换(Linear Transform):x` = Mx
1. 缩放(Scale)
- 相关矩阵:【对角矩阵】
- 矩阵表示:
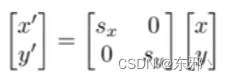
2. 对称/反射(Reflection)
- 相关矩阵:【单位矩阵】
- 矩阵表示:
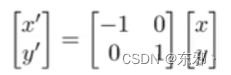
3. 切变(Shear)
- 定义:其中一个方向发生变化,另一方向保持不变
- 矩阵表示:
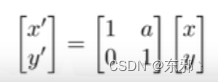
4. 旋转(Rotation)
- 相关矩阵:【推导矩阵R】
- 矩阵表示:
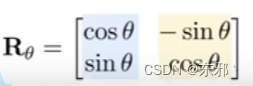
- 负角度旋转:
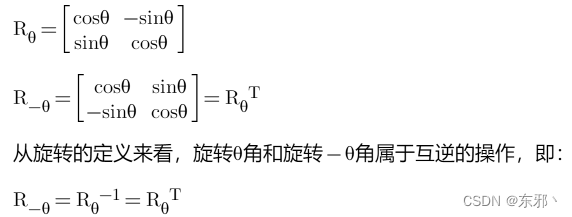
5. 齐次坐标(Homogeneous Coordinates)
- 用途:在图形学中用于统一所有的变换方式
6. 平移(Translation)
- 特点:无法仅通过简单的矩阵相乘获取到平移后的位置(因为平移的坐标只和其对应方向的坐标相关,比如x1 =x+Tx而不是 x1=ax+by)
- 解决方式:新增一个维度
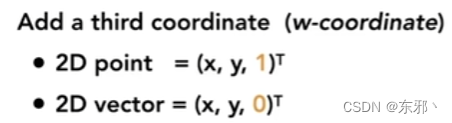
- 矩阵表示:
-
通过仿射变换(Affine Map)表示:
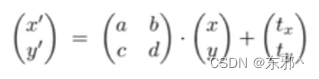
-
通过齐次坐标(Homogeneous Coordinates)表示:
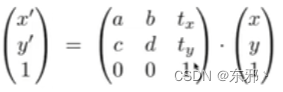
-
- 流程:先线性变换,再进行平移
- 新增维度0、1具体意义:
- 向量新增维度为0:因为向量平移具有不变性,因此矩阵相乘后不希望发生改变,所以设置为0
- 点新增维度为1:可以通过向量与点的相加减来下定义

7. 逆变换(Inverse Transform)
- 定义:和变换做相反的操作(如a->b,则逆变换为b->a)
8. 复合变换(Compose Transform)
- 定义:经过有限次的单个变换操作的总称
9. 分解变换(Decompose Transform)
- 定义:经过有限次的单个变换操作的总称
- 用途:用于对一个非原点的图形进行非平移变换
- 分解特点:先将图形平移回原点,然后经过一系列变换后,再平移回原来的位置
10. 视图变换(Viewing/Camera Transform)
- 定义:将3D物体转化到3D世界中的2D视图中
- 流程:
- 将物体放置于世界坐标系
- 调整相机的位置到原点
- 通过投影变换将3D物体映射并以2D形式表现出来
- 要点:相机、三维物体、投影后的二维平面
- 相机(Camera)
- 需要将相机由任一点移动到原点(0,0,0),对应的矩阵变换应该先平移后旋转
- 由相机所在轴(e,g,t)旋转为(x,y,z)麻烦,可以逆向思维从(x,y,z)旋转到相机所在轴(e,g,t)

- 投影变换(Projection Transform)
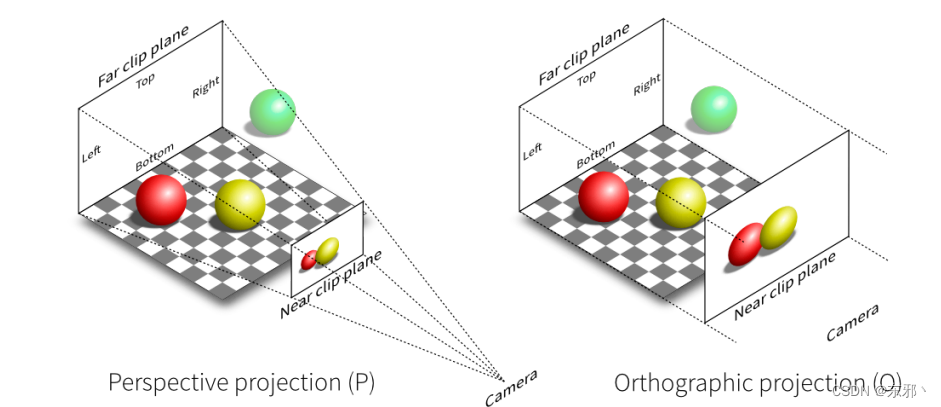
- 正交投影(Orthofraphic Projection)
- 性质:大小始终一致
- 流程:
- 将相机设置/移动到原点,看向z轴的负方向,向上为y轴
- 忽略掉z坐标轴,将得到一个只有x,y轴的2D图形
- 将2D图形的大小规范化为-1到1
- 物体:
- 平移物体中心到原点,然后进行缩放
- 矩阵计算如下(r为右、l为左、t为上、b为下、n为前/近、f为远/后),左起第一个矩阵为缩放,第二个矩阵为平移
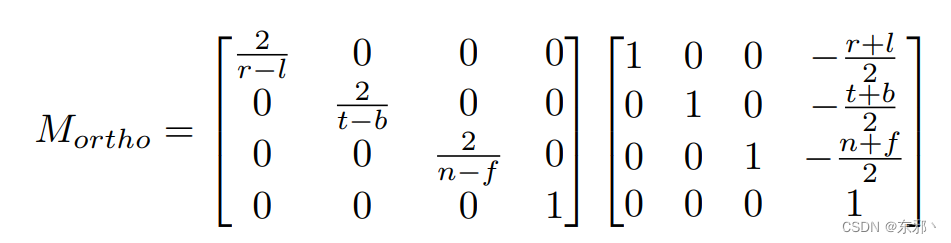
- 透视投影(Perspective Projection)
- 性质:近大远小、原平行线延长会相交
- 流程:
- 将透视投影的四棱锥通过“挤压”成长方体
- 将挤压后的长方体做正交投影
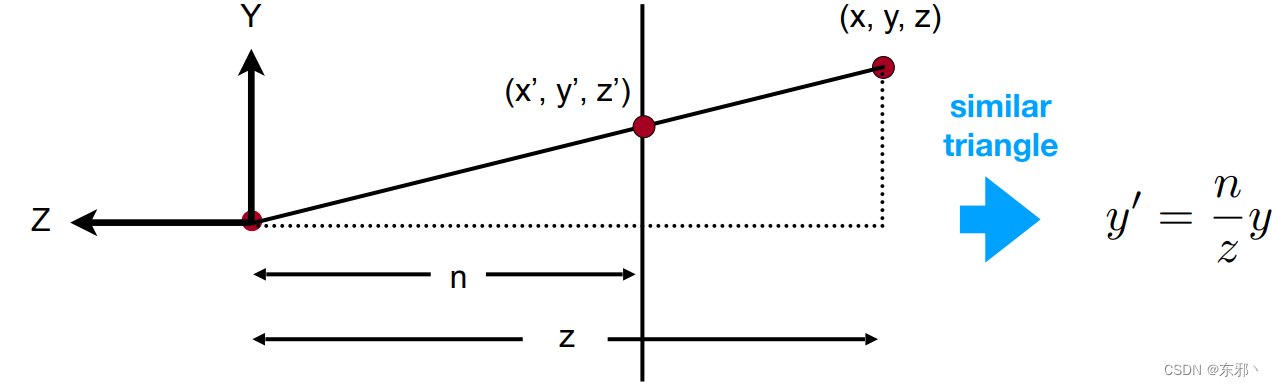
- 挤压
- 因为一个点同乘一个常数,点不变,因此y`=ny
- 近平面的点经过“挤压”后均不变
- 远平面的点经过“挤压”后,z方向值不变
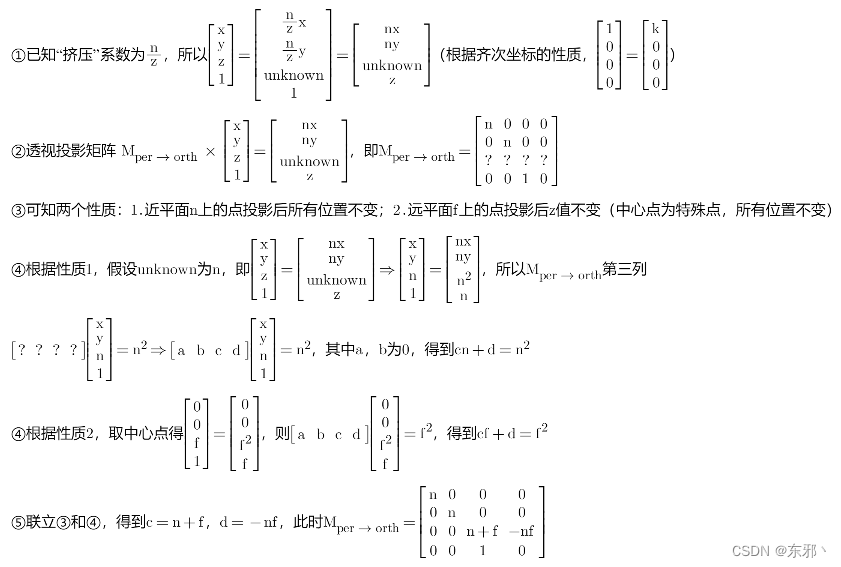
- 推导透视投影矩阵
- 正交投影(Orthofraphic Projection)