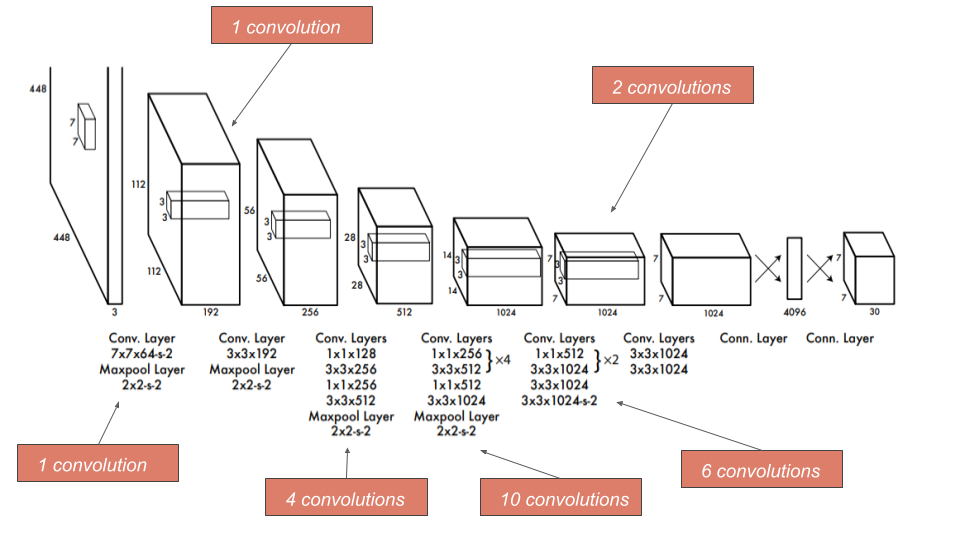
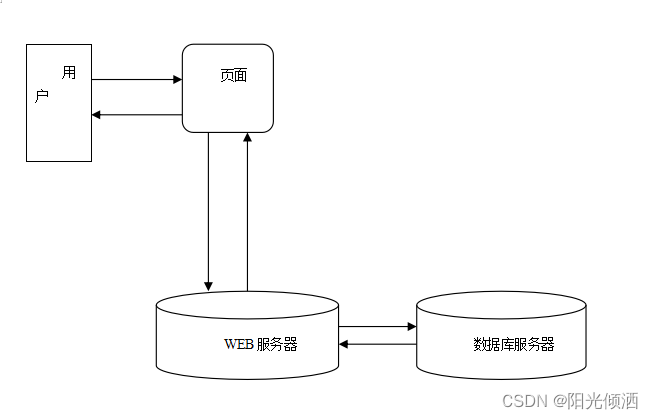
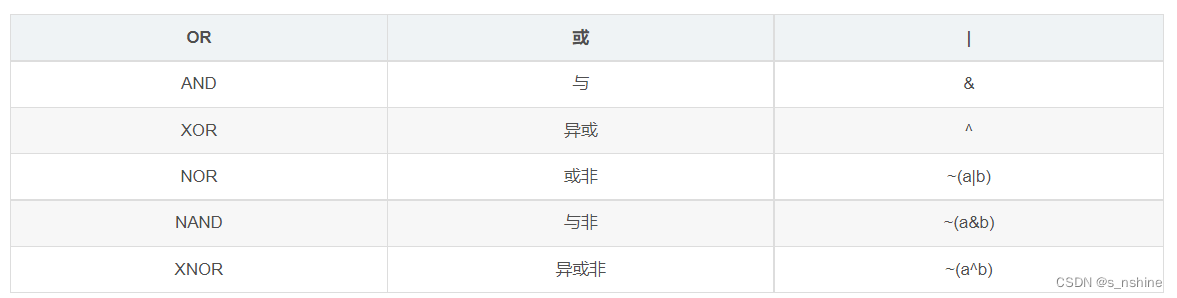
最近复习opencv的东西, 看到camshift
https://www.youtube.com/watch?v=a9KZjQ4e6IA&list=PL6Yc5OUgcoTmTGACTa__vnifNA744Cz-q&index=30
https://medium.com/@claudio.vindimian/understanding-and-implementing-the-camshift-object-tracking-algorithm-python-81587c24eda8
http://opencv.jp/opencv-1.0.0_org/docs/papers/camshift.pdf


协方差矩阵为
[
a
b
2
b
2
c
]
\begin{bmatrix} a & \frac{b}{2} \\ \frac{b}{2} & c \\ \end{bmatrix}
[a2b2bc]
算特征值得到 l 2 l^2 l2, w 2 w^2 w2, 特征值是在坐标投影在特征向量上的方差, 到均值距离的平方再平均, 所以 l , w l, w l,w 并不是最远偏离的距离, 而是一个平均衡量单位
求 θ \theta θ把特征值代进去, 由于特征矩阵的行列式为0, 所以用第一行可以把第二行消为0, 代入特征值用第一行的方程就可以了
( a − c − b 2 + ( a − c ) 2 ) ∗ x + b ∗ y = 0 (a - c - \sqrt{b^2 + (a-c)^2}) * x + b*y= 0 (a−c−b2+(a−c)2)∗x+b∗y=0
t a n θ = y x = b 2 + ( a − c ) 2 − ( a − c ) b tan\theta = \frac{y}{x} = \frac{\sqrt{b^2+(a-c)^2}-(a-c)}{b} tanθ=xy=bb2+(a−c)2−(a−c)
运用2倍角
t
a
n
2
θ
=
2
t
a
n
θ
1
−
t
a
n
2
θ
tan2\theta = \frac{2tan\theta}{1-tan^2\theta}
tan2θ=1−tan2θ2tanθ
最后就得论文里面 θ \theta θ的求法,
总结一下camshift 跟PCA 一样, 都是建立在协方差矩阵上的, 协方差矩阵中的值代表某维与某维之间的关系, 如何大于0就是正相关, 小于0就是负相关, 有了协方差矩阵就可以求他的特征值和特征向量, 特征值代表在对应特征向量上投影的偏离程度, 最大特征值对应的特征向量就是投影散得最开的方向, 跟PCA 一个原理, 有了最大特征向量, 就可以求得旋转方向