目录

​编辑

1、按位与操作

2、按位或操作

3、取反运算

4、异或运算 不同为1，相同为0

​编辑

5、左移运算

6、右移运算

常见用途：

C语言位运算讲解：

---

位运算（包括OR,AND,XOR,NOR,NAND,XNOR，以及&0xFF等常见应用）
位运算是C语言的重要特点，是其他计算机高级语言所没有的，位运算是以二进制为对象的运算，二进制表示法与计算机内存完全对应，每个单元（位）都可以设置成开(1)或关(0)。而且位运算比正常的运算符速度要快很多，因为位运算是一种底层的运算，但是理解起来会偏难一些。

其他补充：

1、位运算符中除~外，均为耳目运算符

2、运算只能是整型或者字符型的数据，不然会报错

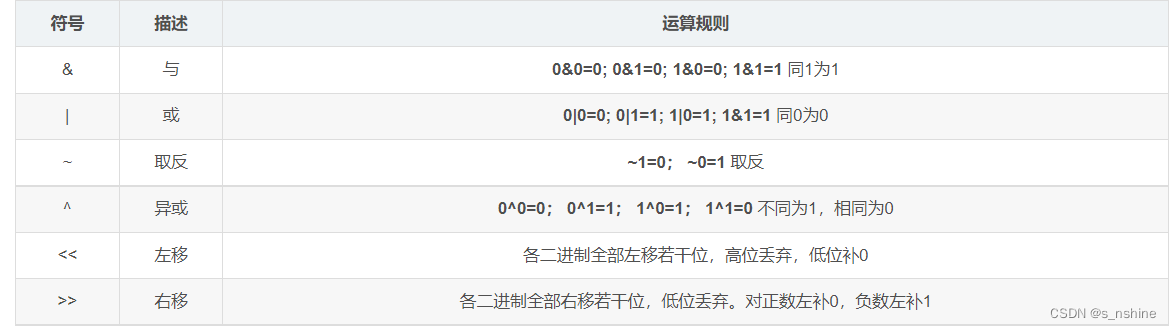
常见的位运算符

1、按位与操作

 例如: 7&5的结果为5，计算如:

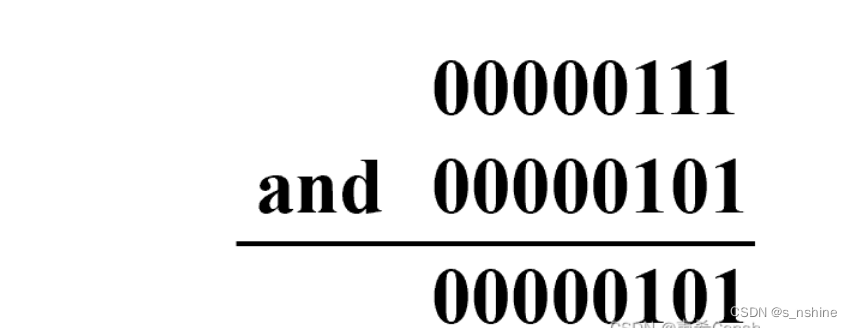
常见用途：

清零: 如果想将一个单元清零，让其与一个各位都为0的数值相与

取数（常见保留低八位,或者低16位，图像中常见）:

例如，X=1001110101， 进行操作 X&0xFF 之后得到 01110101 Y=10000000000100111，进行操作 Y&0xFFFF 之后得到 0000000000100111

2、按位或操作

例如: 7|5的结果为7，计算如:

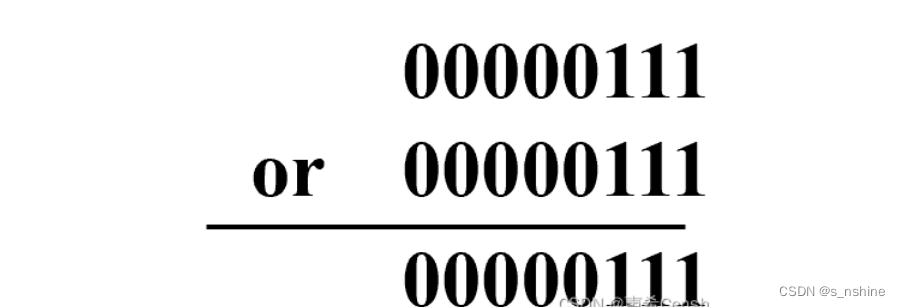
常见用途：

负数补码

将一个数的某些‘’位‘置为1 例如：把Z=10100110的低4位的数置为1，Z|00001111即可满足目的。

3、取反运算

例如：~7的结果为-8，计算如:

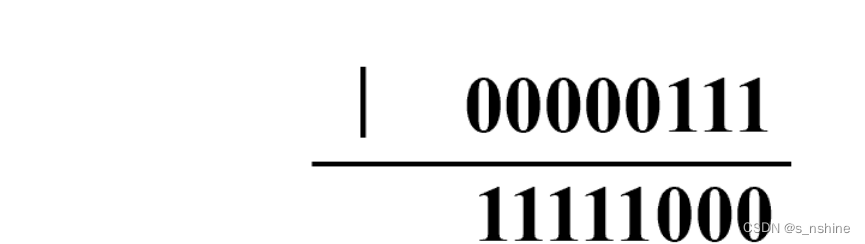
常见用途：

使一个数的最低位为0，例如：Q&~1, ~1的值为1111111111111110，在与操作之后，最低位一定为0，~的优先级高于算数运算符、关系运算符、逻辑运算符等

4、异或运算 不同为1，相同为0

例如：10^-9的结果为-3 计算如：

即 0000 1010 ^ 1111 0111 = 1111 1101(补码) 原码即为1000 0011 即10^-9 = -3

常见用途：

使特定位翻转：例如Q=10110110，使Q低4位翻转，用X ^ 0000 1111 = 1011 1001即可得到

与0相异，保留原值： Q^0000 0000 = 10110110

交换A和B：

不推荐以上这个交换方式，相应还有一种加减的方法交换数值（如下所示），同样不推荐，难懂且效率不如中间临时变量的方法。

5、左移运算

 将一个运算对象的各二进制位全部左移若干位（左边的二进制位丢弃，右边补0）

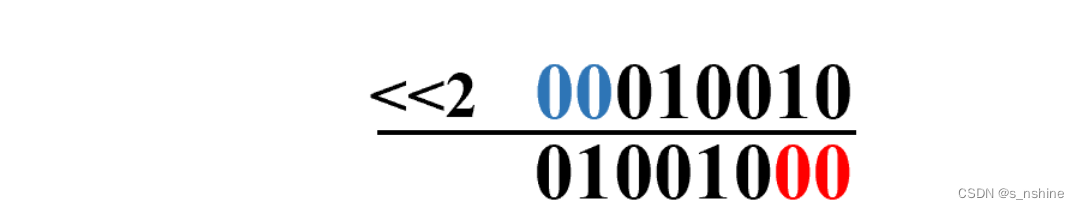
例如：X =18; X= X <<2，结果为72 计算如：

上述左移一位后X=X*2; 若左移时舍弃的高位不包含1，则每左移一位，相当于该数乘以2。

6、右移运算

将一个数的各二进制位全部右移若干位，正数左补0，负数左补1，右边丢弃

例如：X =18; X= X >>2，结果为4 计算如：

常见用途：

操作数每右移一位，相当于该数除以2（向下取整）。

注意：

移位运算符在C++中会生成一个新值，但不回修改原来的值，例如：

上述代码两次输出的值均为108，即不会修改x的值，表达式x<<2使用x的值来生成一个新的值，就像x+3会申城一个新值，但不会修改x一样，如果要用移位运算符来修改变量的值，则必须使用赋值运算符，可以使用常规的赋值运算符或者<=运算符，如：

位运算的一些其他应用：

 1、判断奇偶数

对于除0之外的任何数，使用X&1==1作为逻辑判断即可，例如：

2、判断某个二进制是否为1

 //例如判断x的第五位是否为1，十六进制的0x10转换为二进制是0001 0000

3、求平均数

 

4、判断两个数是否异号

5、数据加密

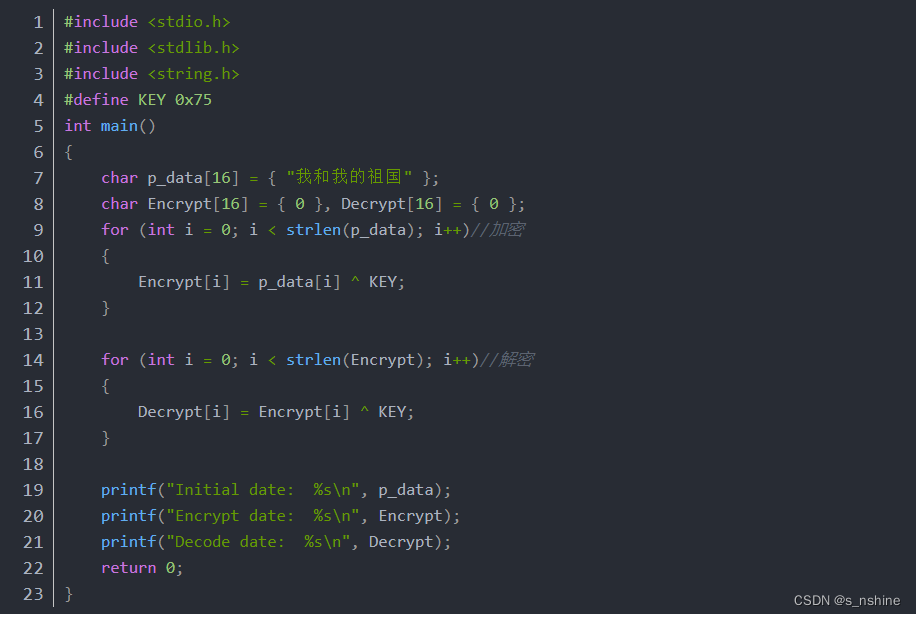
上述输出结果为：

Initial date: 我和我的祖国
Encrypt date: 户细户辣虖
Decode date: 我和我的祖国

6、取绝对值(效率高)

或者

其他操作参见https://zhuanlan.zhihu.com/p/148790042

另外对于一些符号，例如OR,AND,XOR,NOR,NAND,XNOR以及其实现等简单说一下

 

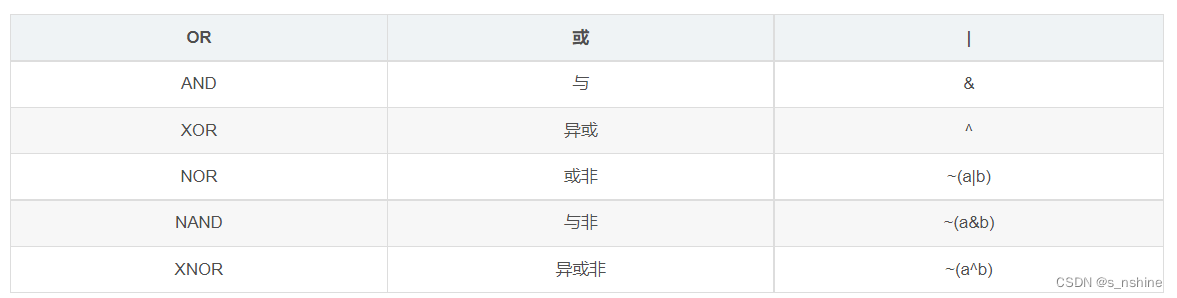
C语言位运算讲解：

//定义两个8位的变量
unsigned char Byte1 = 0x15;
unsigned char Byte2 = 0xf6;

//一个字节分为8位，叫法不一，都是一个意思
//叫法一：位7    位6    位5    位4    位3    位2    位1    位0  
//叫法二：Bit7   Bit6   Bit5   Bit4   Bit3   Bit2   Bit1   Bit0  
//叫法三：第8位  第7位  第6位  第5位  第4位  第3位  第2位  第1位
//不建议使用第3种叫法，建议第2种

Byte1 |= (0x01 << 3);        //这句的意思：把Byte1的Bit3置1
Byte2 &= ~(0x01 << 6);        //这句的意思：把Byte2的Bit6置0

/*1、Byte1 |= (0x01 << 3);的计数过程详解：
  1）、|=叫做或等，与+=作用类似，a|=b就是a=a|b，a+=b就是a=a+b。所以Byte1 |= (0x01 << 3);就是Byte1 = Byte1|(0x01 << 3);
  2）、0x01用把8位二进制表示:0000 0001 (注：Byte1是8位的数据，所以使用8位二进制，如果Byte1是16位数据，则使用16位二进制...)
       然后左移3位，就变成了0000 1000。
  3）、Byte1的值是0x15，即0001 0101，Byte1或上(0x01 << 3)，就是0001 0101和0000 1000按位或
        0001 0101
      | 0000 1000
  结果是0001 1101，与Byte1的原值相比，区别就是Bit3被置为了1

  2、Byte2 &= ~(0x01 << 3);的计数过程详解：
  1）、&=叫做与等，a&=b就是a=a&b。所以Byte2 &= ~(0x01 << 3);就是Byte2 = Byte2&(~(0x01 << 3));
  2）、0x01用把8位二进制表示:0000 0001 
       然后左移6位  就变成了 0100 0000
       左移后再取反 就变成了 1011 1111
  3）、Byte2的值是0xf6，即1111 0110，Byte2与上~(0x01 << 6)，就是1111 0110和1011 1111按位与
        1111 0110
      & 1011 1111
  结果是1011 0110，与Byte1的原值相比，区别就是Bit6被置为了0
*/

十六进制数值转换成十进制数值的知识

/*
相关知识:
十六进制数换算成十进制数值的方法
例如：将十六进制数0xAE转换为十进制数

方法一:
转成二进制再换算成十进制二进制:
0xAE的二进制表示：       1   0  1  0   1 1 1 0
各位对应的十进制数值 : 128 64 32 16  8 4 2 1
最终得到十进制数值就是 128  + 32  +  8+4+2 = 174

方法二 : 
十六进制直接换算成十进制数值
0xAE：A即10，E即14，进制为16
所以0xAE等于10x16的1次方 + 14x16的0次方 = 174

*/