1 Math类
1.1 概述
tips:了解内容
查看API文档,我们可以看到API文档中关于Math类的定义如下:

Math类所在包为java.lang包,因此在使用的时候不需要进行导包。并且Math类被final修饰了,因此该类是不能被继承的。
Math类包含执行基本数字运算的方法,我们可以使用Math类完成基本的数学运算。
要想使用Math类我们就需要先创建该类的对象,那么创建对象就需要借助于构造方法。因此我们就需要首先查看一下API文档,看看API文档中针对Math类有没有提供对应的构造方法。通过API文档来查看
一下Math类的成员,如下所示:
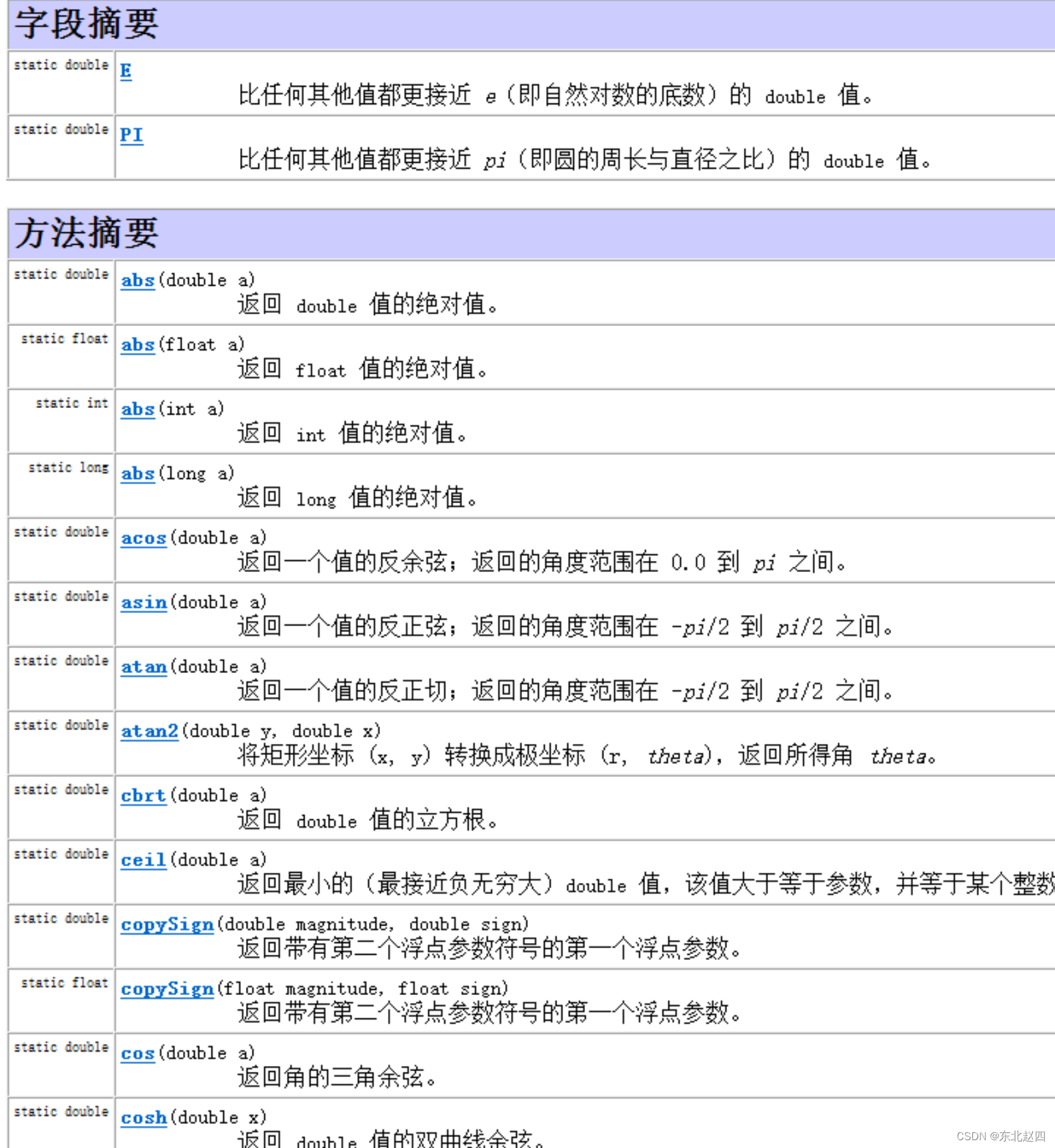
在API文档中没有体现可用的构造方法,因此我们就不能直接通过new关键字去创建Math类的对象。同时我们发现Math类中的方法都是静态的,因此在使用的时候我们可以直接通过类名去调用。在Math类中
定义了很多数学运算的方法,但是我们并不可能将所有的方法学习一遍,我们主要学习的就是一些常见的方法。
1.2 常见方法
tips:重点讲解内容
常见方法介绍
我们要学习的Math的常见方法如下所示:
public static int abs(int a) // 返回参数的绝对值
public static double ceil(double a) // 返回大于或等于参数的最小整数
public static double floor(double a) // 返回小于或等于参数的最大整数
public static int round(float a) // 按照四舍五入返回最接近参数的int类型的值
public static int max(int a,int b) // 获取两个int值中的较大值
public static int min(int a,int b) // 获取两个int值中的较小值
public static double pow (double a,double b) // 计算a的b次幂的值
public static double random() // 返回一个[0.0,1.0)的随机值案例演示
接下来我们就来演示一些这些方法的执行效果,如下所示:
public class MathDemo01 {
public static void main(String[] args) {
// public static int abs(int a) 返回参数的绝对值
System.out.println("-2的绝对值为:" + Math.abs(-2));
System.out.println("2的绝对值为:" + Math.abs(2));
// public static double ceil(double a) 返回大于或等于参数的最小整数
System.out.println("大于或等于23.45的最小整数位:" + Math.ceil(23.45));
System.out.println("大于或等于-23.45的最小整数位:" + Math.ceil(-23.45));
// public static double floor(double a) 返回小于或等于参数的最大整数
System.out.println("小于或等于23.45的最大整数位:" + Math.floor(23.45));
System.out.println("小于或等于-23.45的最大整数位:" + Math.floor(-23.45));
// public static int round(float a) 按照四舍五入返回最接近参数的int
System.out.println("23.45四舍五入的结果为:" + Math.round(23.45));
System.out.println("23.55四舍五入的结果为:" + Math.round(23.55));
// public static int max(int a,int b) 返回两个int值中的较大值
System.out.println("23和45的最大值为: " + Math.max(23, 45));
// public static int min(int a,int b) 返回两个int值中的较小值
System.out.println("12和34的最小值为: " + Math.min(12 , 34));
// public static double pow (double a,double b)返回a的b次幂的值
System.out.println("2的3次幂计算结果为: " + Math.pow(2,3));
// public static double random()返回值为double的正值,[0.0,1.0)
System.out.println("获取到的0-1之间的随机数为: " + Math.random());
}
}运行程序进行测试,控制台输出结果如下:
-2的绝对值为:2
2的绝对值为:2
大于或等于23.45的最小整数位:24.0
大于或等于-23.45的最小整数位:-23.0
小于或等于23.45的最大整数位:23.0
小于或等于-23.45的最大整数位:-24.0
23.45四舍五入的结果为:23
23.55四舍五入的结果为:24
23和45的最大值为: 45
12和34的最小值为: 12
2的3次幂计算结果为: 8.0
获取到的0-1之间的随机数为: 0.73224841317459581.3 算法小题(质数)
需求:
判断一个数是否为一个质数
代码实现:
public class MathDemo2 {
public static void main(String[] args) {
//判断一个数是否为一个质数
System.out.println(isPrime(997));
//997 2~996 995次
}
public static boolean isPrime(int number) {
int count = 0;
for (int i = 2; i <= Math.sqrt(number); i++) {
count++;
if (number % i == 0) {
return false;
}
}
System.out.println(count);
return true;
}
}1.4 算法小题(自幂数)
自幂数,一个n位自然数等于自身各个数位上数字的n次幂之和
举例1:三位数 1^3 + 5^3 + 3^3 = 153
举例2:四位数 1^4 + 6^4 + 3^4 + 4^3 = 1634
如果自幂数是:
-
一位自幂数,也叫做:独身数
-
三位自幂数:水仙花数 四位自幂数:四叶玫瑰数
-
五位自幂数:五角星数 六位自幂数:六合数
-
七位自幂数:北斗七星数 八位自幂数:八仙数
-
九位自幂数:九九重阳数 十位自幂数:十全十美数
要求1:统计一共有多少个水仙花数。
要求2:(课后作业)证明没有两位的自幂数。
要求3:(课后作业)分别统计有多少个四叶玫瑰数和五角星数。(答案:都是3个 )
//水仙花数:100 ~ 999
int count = 0;
//得到每一个三位数
for (int i = 100; i <= 999; i++) {
//个位 十位 百位
int ge = i % 10;
int shi = i / 10 % 10;
int bai = i / 100 % 10;
//判断:
//每一位的三次方之和 跟本身 进行比较。
double sum = Math.pow(ge, 3) + Math.pow(shi, 3) + Math.pow(bai, 3);
if (sum == i) {
count++;
//System.out.println(i);
System.out.println(count);
}
}