题目：

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：

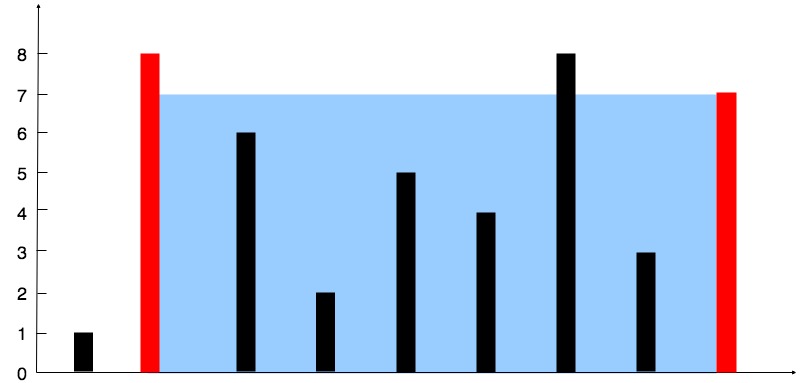
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

提示：

• n == height.length
• 2 <= n <= 105
• 0 <= height[i] <= 104

算法原理：

 盛水量=边界数值的下标相减*两边界中值较小者

1 left指针指定左边界 right指针指定右边界

   用此时的两边界得到一个盛水量mul

2 跳过左右边界中的较小值，每得到一个新的左右边界组合，就重复步骤1得到新的mul，并与最大值作比较，大于则更新最大值

 因为不管左右边界中的任意一方向内移动，做出变更，都会使得宽减小，但是高还未定

   这里假设初始时左边界<右边界

  a 若是左边界不动，右边界向内移动（保留左边界）：

     若右边界数值大于左边界，高则依然是左边界，不变，减小的宽*不变的高-->体积变小

     若右边界数值小于左边界，高则变小，减小的宽*变小的高-->体积变小

     综上，左边界与除了最初右边界以外的任意一个组合，所得盛水量一定小于左边界与最初始右边界所得盛水量，那么这个左边界也就没必要继续进行组合了，left++

 b 若是右边界不动，左边界向内移动（保留右边界）：

    若左边界数值大于右边界，高变成右边界的数值，相较于原来高是左边界的数值，变大

     变大的高*减小的宽-->体积不能确定一定小于最初始的体积

     那么说明右边界有可能与除了最初的左边界以外的数值组合所得体积>初始体积，要保留右边界

 代码实现：

class Solution 
{
public:
    int maxArea(vector<int>& height) 
    {
        int n = height.size();
        int left = 0;
        int right = n-1;
        int Max = 0;
        while(left<right)
        {
            int mul = (right-left)*min(height[left],height[right]);
            Max = max(Max,mul);
            if(height[left]<height[right])
            {
                left++;
            }
            else
            {
                right--;
            }
        }
        return Max;
    }
};