双指针算法大致有以下几个类型
- 对撞指针:一般用来处理两数和问题
- 快慢指针: 一般在链表中用的比较多,如求链表中间结点,链表是否有环等,当然一些非链表题也会用到相关的思想
- 区间划分: 将数组分成两个不同性质的两个部分
一、对撞指针
1.盛⽔最多的容器(点击这里,直达题目)
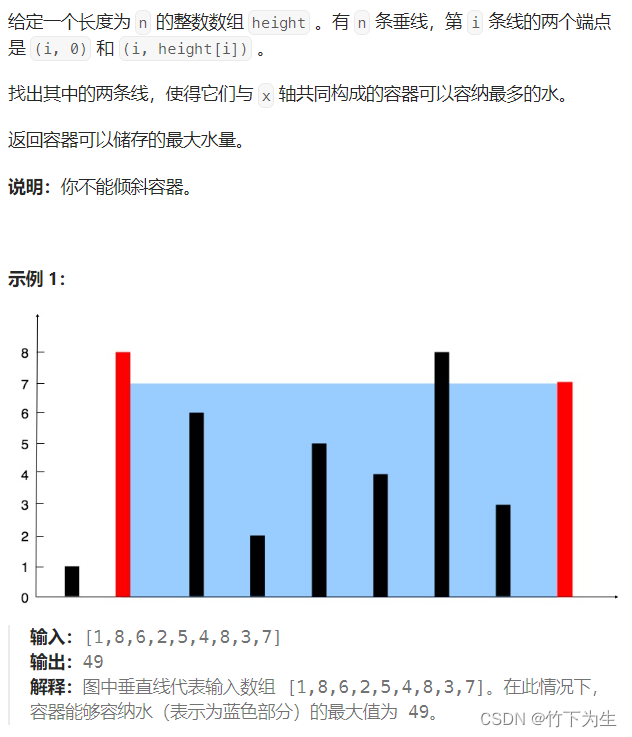
看到这题,最直接的想法就是暴力,两层for循环直接枚举左右端点,在所有的情况中找到最大值,时间复杂度是O(n^2),过不了,那么我们怎么优化时间复杂度?
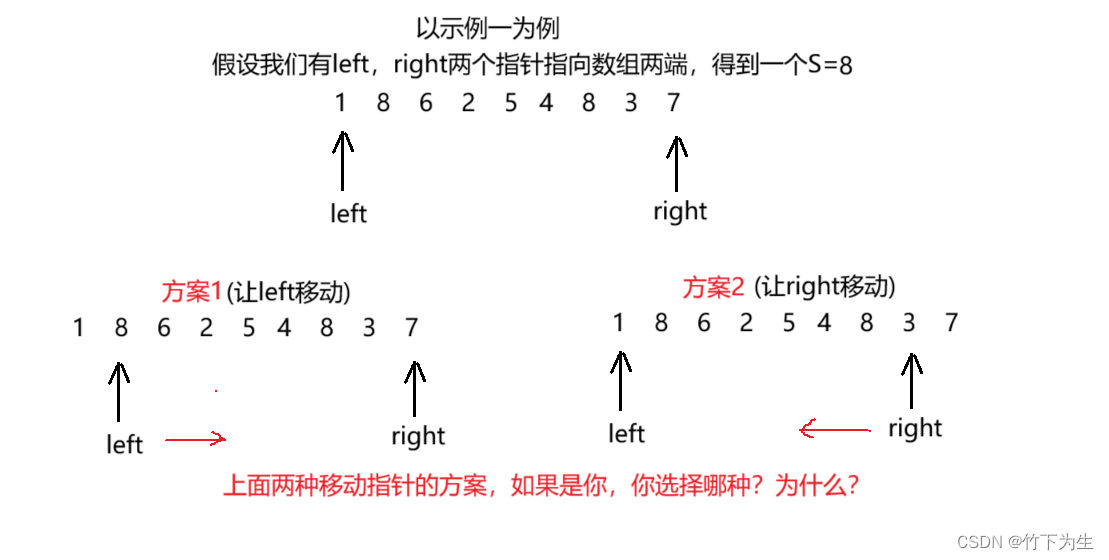
这两个问题就是双指针思路的关键,这里就解释一下为什么是方案1,因为S=h * w,而此时的w只能减小,那么我们如果想让S变大,就只能将h变大,而h是由两边较低的高度决定的,如果我们移动较高的那条边,那么h就会受限于较低的那条边的高度,所以S只会变小,这就导致我们只能移动较低的那条边,而这也就能保证这个算法的正确性,即我们是将没有枚举到的情况排除了,并不是说枚举漏了,代码如下
class Solution {
public:
int maxArea(vector<int>& height) {
int left=0,right=height.size()-1,ans=0;
while(left<right)
{
ans=max(ans,min(height[left],height[right])*(right-left));
if(height[left]<height[right])
left++;
else
right--;
}
return ans;
}
};2.和为s的两个数字(点击这里,直达题目)

这题当然也是可以直接暴力枚举,两层for循环结束,时间复杂度是O(n^2),但是题目中给的排序条件我们没有用上,那么我们如何利用这个条件优化时间复杂度?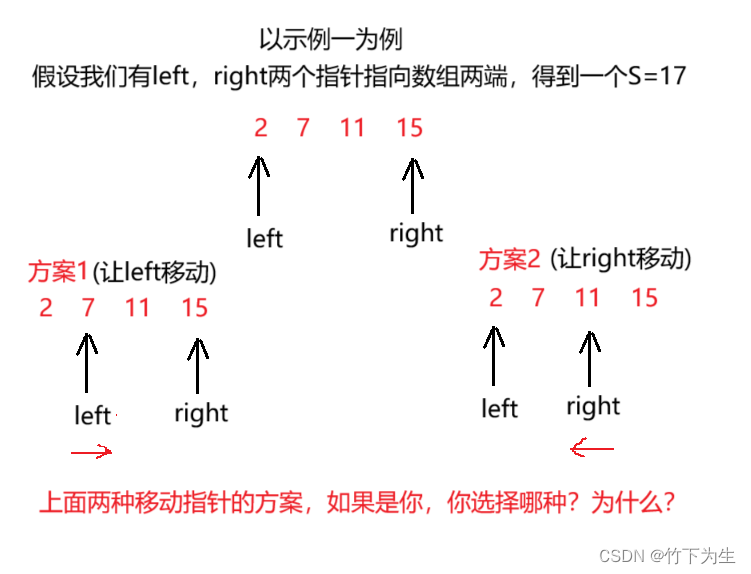
选方案2,理由如下
因为s=17,而target=9,所以我们需要让s变小,而中间的元素都比nums[left]大,比nums[right]小,如果移动left,只能让s更大,所以我们移动right,让s减小,如果遇到s<target的情况,就移动left,理由同上,而我们能这么做的根本原因在于数组有序,(思路的正确性的分析同上一题)
代码如下
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
int left=0,right=nums.size()-1;
while(left<right){
int sum=nums[left]+nums[right];
if(sum==target) return {nums[left],nums[right]};
if(sum<target) left++;
else right--;
}
return {};
}
};当然我们还能求s<target的数字对个数,s>target的数字对个数等等,同样的分析方法,就留给大家做练习了。
总结一下:能否使用对撞指针,主要看是否满足"单调性",即在固定其中一个指针的情况下,left和right从逻辑上来说只能有一个发生移动,当我们不确定时,就照着上面的分析方法试试看
二、快慢指针
这个一般在链表中用的比较多,很多链表的经典题目都会用到,这里就不细讲在链表中的应用了,一般链表的题目大家都很容易想到这个思想,但是一旦题目脱离了链表,我们基本就不会有意识的想到这种思想,如下面这道题
快乐数(点击这里,直达题目)

这道题的关键就在于无限循环,因为如果你对链表很熟悉的话,你就会想到链表有环的相关问题,然后你就会想到快慢指针,而这就是这道题的解法
好,我们来看一下这道题,就是判断数是否是快乐数,如果是,那么在经过一段重复的操作之后,会变为1,如果不是,则会一直循环,本质不是和判断链表是否有环一摸一样的问题吗?没环,则链表会走到NULL,有环,则一直循环。至于有人说的无限循环,也可能是走一直不重复的数字,这个问题后面会简单证明一下,这里就先默认要么为1,要么循环
代码如下
class Solution {
public:
int Get(int x){
int res=0;
while(x){
res+=(x%10)*(x%10);
x/=10;
}
return res;
}
bool isHappy(int n) {
int fast=Get(n),slow=n;
while(fast!=slow)//如果相等停下来,1也可以看成循环,只是循环的数字一直是1
{
slow=Get(slow);//相当于链表中slow往后走一步
fast=Get(Get(fast));//相当于链表中fast往后走两步
}
return slow==1;//判断是否是快乐数
}
};
总结一下:快慢指针的思想不是只能出现在链表中,我们要能通过题目给的信息找出它和链表题之间的关系,实现知识的迁移变形
三、区间划分
移动零(点击这里,直达题目)

我们的思路是根据题目要求维护三个区间,被双指针分割出来的三个区间
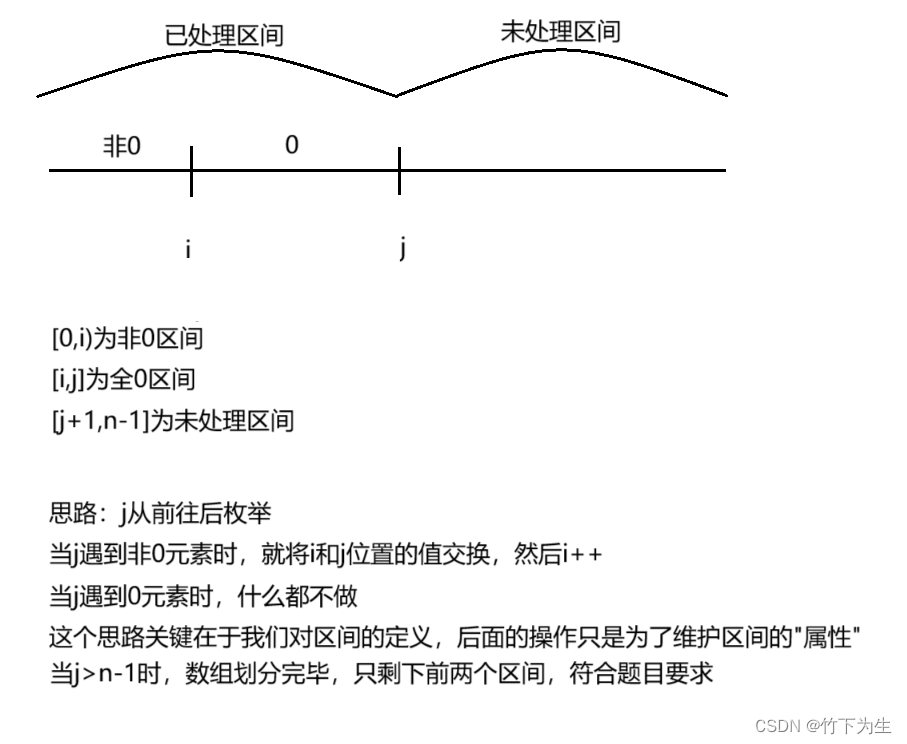
代码如下
class Solution {
public:
void moveZeroes(vector<int>& nums) {
for(int i=0,j=0;j<nums.size();j++)
if(nums[j])
swap(nums[i++],nums[j]);
}
};这题的思路其实和快排中,选定目标值target,然后将数组分为<=target和>target两部分的实现一样,都是划分数组,维护区间,忘记的可以去回顾一下
总结一下:当遇到要将数组划分区间的题目时,可以想想能不能用双指针来做
当然这题用快慢指针的思想也能做,代码如下
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int j=0;
for(int i=0;i<nums.size();i++)
if(nums[i])
nums[j++]=nums[i];
while(j<nums.size())
nums[j++]=0;
}
};