1.常微分方程
常微分方程 (ODE) 包含与一个自变量 t(通常称为时间)相关的因变量 y 的一个或多个导数。此处用于表示 y 关于 t 的导数的表示法对于一阶导数为
y
′
,对于二阶导数为
y
′′,依此类推。ODE 的阶数等于 y 在方程中出现的最高阶导数。
例如,这是一个二阶 ODE:
y
′′ = 9
y
在初始值问题中,从初始状态开始解算 ODE。利用初始条件 y
0 以及要在其中求得答案的时间段(t0,tf ),以迭代方式获取解。在每一步,求解器都对之前各步的结果应用一个特定算法。在第一个这样的时间步,初始条件将提供继续积分所需的必要信息。最终结果是,ODE 求解器返回一个时间步向量t
= [
t
0
,
t
1
,
t
2
, ...,
t
f ]
以及在每一步对应的解
y = [y0
,
y
1
,
y
2
, ...,
yf ]。
2.ODE 的类型
MATLAB 中的 ODE 求解器可解算以下类型的一阶 ODE:
• y
′ =
f(t
,
y
)形式的显式 ODE。
• M (t
,
y )y
′ =
f (t
,
y
)形式的线性隐式 ODE,其中
M t
, y 为非奇异质量矩阵。该质量矩阵可以是时间或状态依赖的矩阵,也可以是常量矩阵。线性隐式 ODE 涉及在质量矩阵中编码的一阶 y 导数的线性组合。
线性隐式 ODE 可随时变换为显式形式 y′ = 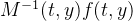 。不过,将质量矩阵直接指定给 ODE 求解器可避免这种既不方便还可能带来大量计算开销的变换操作。
。不过,将质量矩阵直接指定给 ODE 求解器可避免这种既不方便还可能带来大量计算开销的变换操作。
• 如果 y′ 的某些分量缺失,则这些方程称为微分代数方程或 DAE,并且 DAE 方程组会包含一些代数变量。代数变量是导数未出现在方程中的因变量。可通过对方程求导来将 DAE 方程组重写为等效的一阶ODE 方程组,以消除代数变量。将 DAE 重写为 ODE 所需的求导次数称为微分指数。
ode15s 和ode23t
求解器可解算微分指数为 1 的 DAE。
• f( t
,
y
,
y
′ )= 0 形式的完全隐式 ODE。完全隐式 ODE 不能重写为显式形式,还可能包含一些代数变量。ode15i
求解器专为完全隐式问题(包括微分指数为 1 的 DAE)而设计。
可通过使用 odeset
函数创建 options 结构体,来针对某些类型的问题为求解器提供附加信息。
3.ODE 方程组
您可以指定需要解算的任意数量的 ODE 耦合方程,原则上,方程的数量仅受计算机可用内存的限制。如果方程组包含 n 个方程,
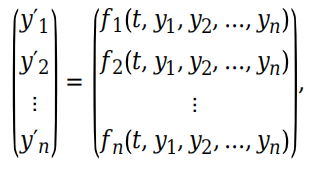
则用于编写该方程组代码的函数将返回一个向量,其中包含 n 个元素,对应于 y
′
1
,
y
′
2
, … ,
y
′
n 值。例如,考虑以下包含两个方程的方程组
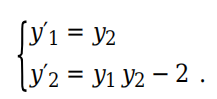
用于编写该方程组代码的函数为
function dy = myODE(t,y)
dy(1) = y(2);
dy(2) = y(1)*y(2)-2;
end4.高阶 ODE
MATLAB ODE 求解器仅可解算一阶方程。您必须使用常规代换法,将高阶 ODE 重写为等效的一阶方程组
y
1
=
y
y
2
=
y
′
y
3
=
y
′′
⋮
y
n
= 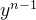 .
.
这些代换将生成一个包含 n 个一阶方程的方程组
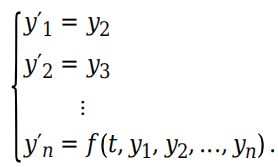
例如,考虑三阶 ODE :y′′′ − y′′y + 1 = 0,并使用代换法
y
1
=
y
y
2
=
y
′
y
3
=
y
′′
生成等效的一阶方程组
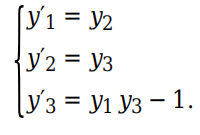
此方程组的代码则为
function dydt = f(t,y)
dydt(1) = y(2);
dydt(2) = y(3);
dydt(3) = y(1)*y(3)-1;
end5.复数 ODE
考虑复数 ODE 方程
y
′ =
f (t
,
y )
,
其中 y
=
y
1
+
iy
2。为解算该方程,需要将实部和虚部分解为不同的解分量,最后重新组合相应的结果。从概念上讲,这类似于
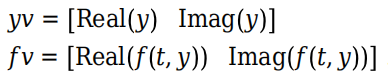
例如,如果 ODE 为
y
′ =
yt
+ 2
i
,则可以使用函数文件来表示该方程:
function f = complexf(t,y)
f = y.*t + 2*i;
end
然后,分解实部和虚部的代码为
function fv = imaginaryODE(t,yv)
% Construct y from the real and imaginary components
y = yv(1) + i*yv(2);
% Evaluate the function
yp = complexf(t,y);
% Return real and imaginary in separate components
fv = [real(yp); imag(yp)];
end
在运行求解器以获取解时,初始条件 y0
也会分解为实部和虚部,以提供每个解分量的初始条件。
y0 = 1+i;
yv0 = [real(y0); imag(y0)];
tspan = [0 2];
[t,yv] = ode45(@imaginaryODE, tspan, yv0);
获得解后,将实部和虚部分量组合到一起可获得最终结果。
y = yv(:,1) + i*yv(:,2);6.基本求解器选择
ode45 适用于大多数 ODE 问题,一般情况下应作为您的首选求解器。但对于精度要求更宽松或更严格的问题而言,
ode23
、
ode78
、
ode89
和
ode113
可能比
ode45
更加高效。
一些 ODE 问题具有较高的计算刚度或难度。术语“刚度”无法精确定义,但一般而言,当问题的某个位置存在标度差异时,就会出现刚度。例如,如果 ODE 包含的两个解分量在时间标度上差异极大,则该方程可能是刚性方程。如果非刚性求解器(例如
ode45)无法解算某个问题或解算速度极慢,则可以将该问题视为刚性问题。如果您观察到非刚性求解器的速度很慢,请尝试改用
ode15s 等刚性求解器。在使用刚性求解器时,可以通过提供 Jacobian 矩阵或其稀疏模式来提高可靠性和效率。
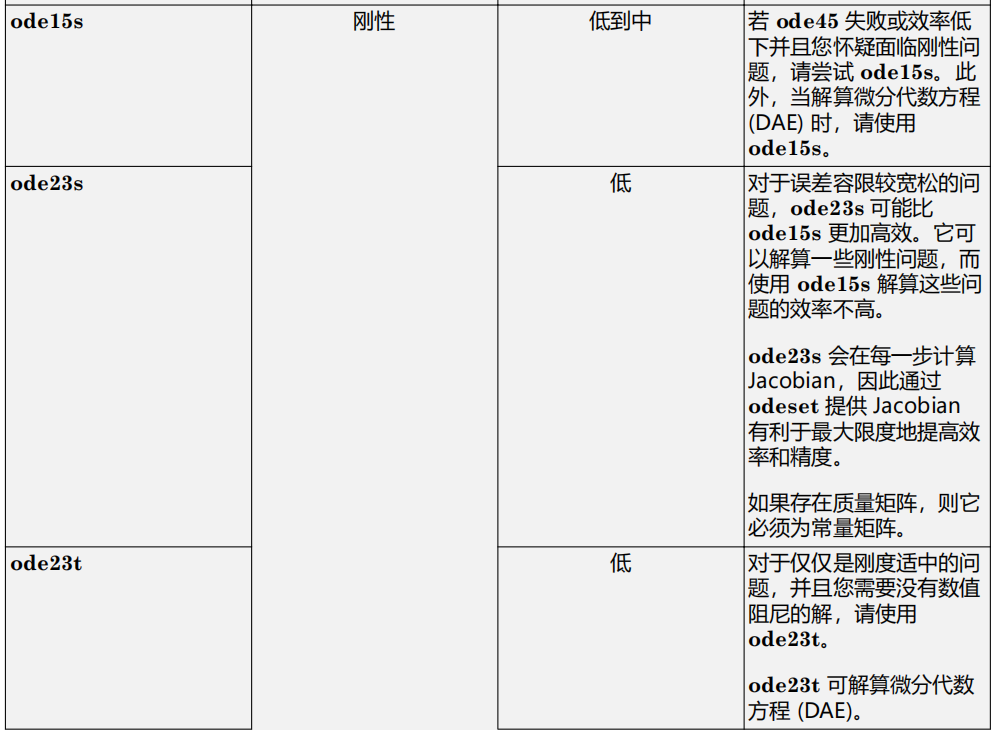
下表提供了关于何时使用每种不同求解器的一般指导原则。
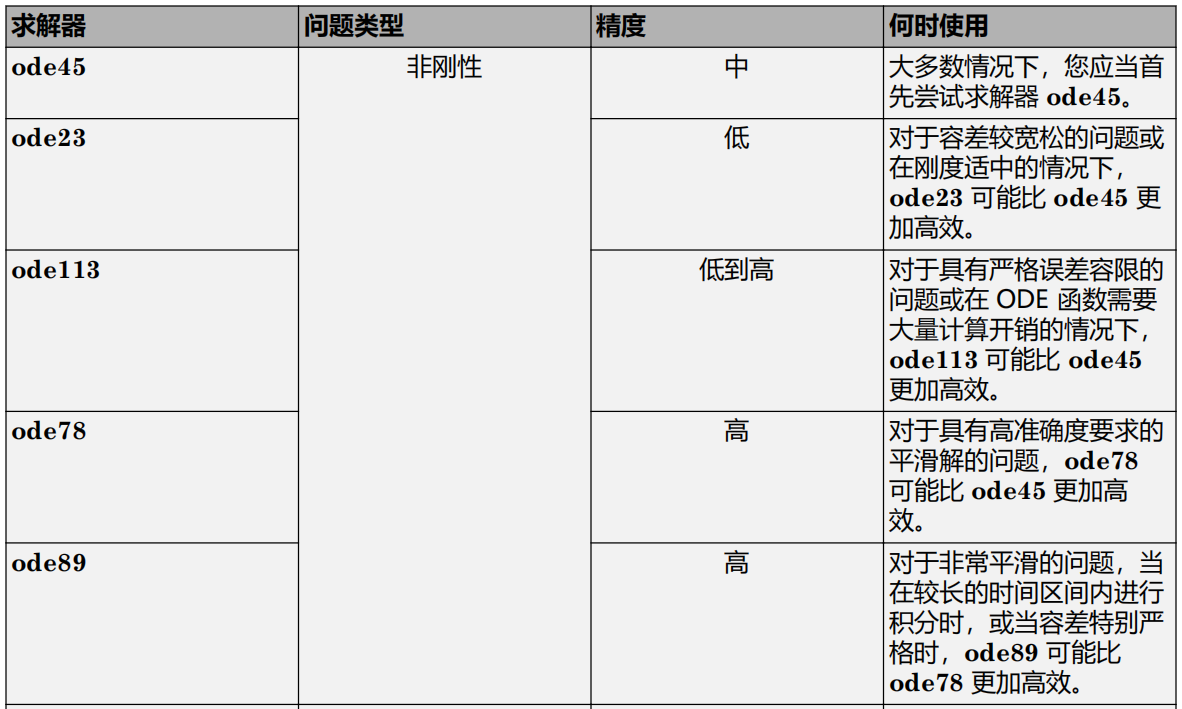

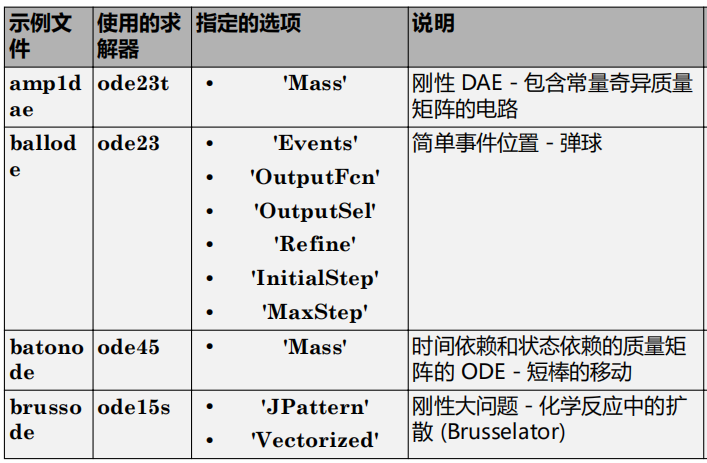
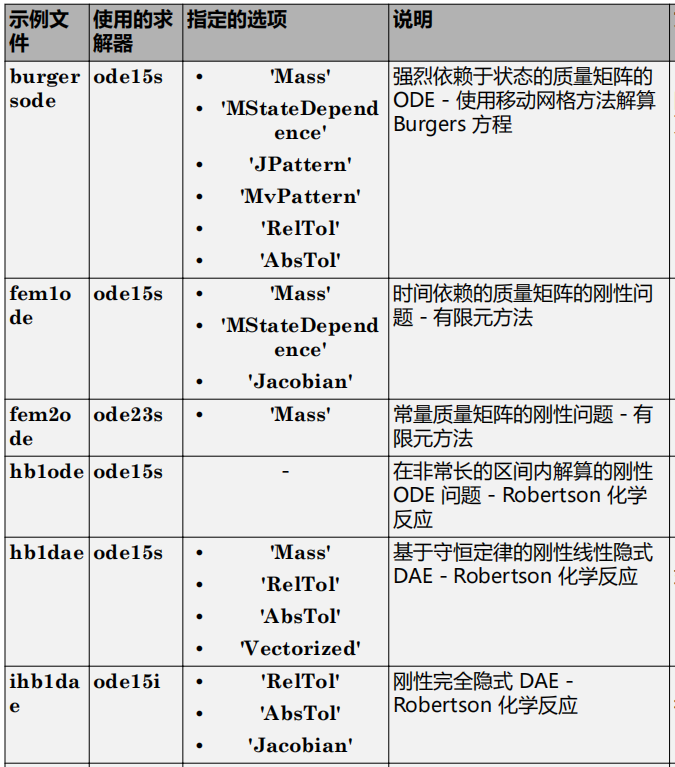
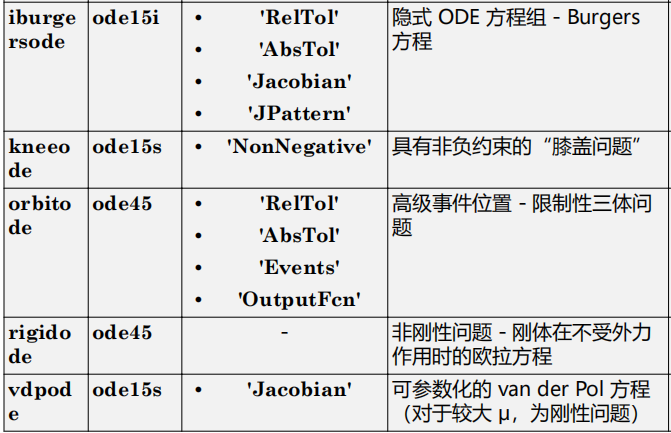
7.ODE 示例和文件摘要
有几个示例文件可用作大多数 ODE 问题的有用起点。要运行微分方程示例应用,以便轻松浏览和运行示例,请键入
odeexamples
要打开单独的示例文件进行编辑,请键入
edit exampleFileName.m
要运行示例,请键入
exampleFileName
此表包含可用的 ODE 和 DAE 示例文件及其使用的求解器和选项的列表。其中包含示例子集的链接,这些示例也已直接发布在文档中。