反向传播求变量导数
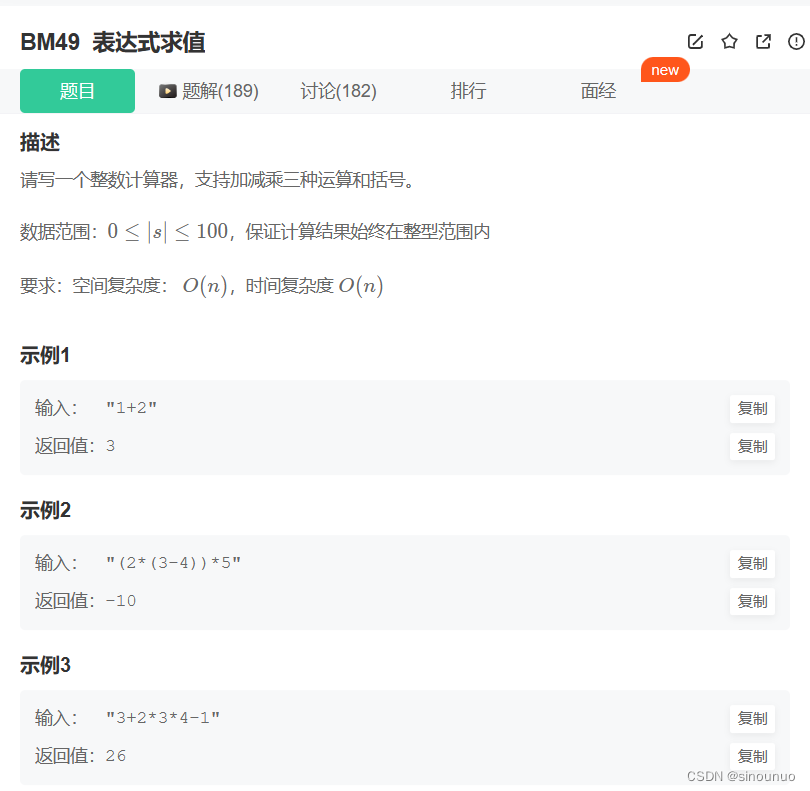
- 1. 相关习题
- 2. 推导流程
- 2.1 相关公式
- 2.3 变量导数求解
- 3. 代码实现
- 3.1 参数对应
- 3.2 代码实现
- 以前只知道反向传播通过链式法则实现
- 今天看书发现图片上求出来的值自己算不出来
- 所以自己算了一下,记录一下,并运行了书中的代码
- 相关书籍:[图灵程序设计丛书].深度学习入门:基于Python的理论与实现
1. 相关习题

2. 推导流程
2.1 相关公式
f = a ∗ b g = c ∗ d h = f + g = a ∗ b + c ∗ d i = h ∗ e = ( f + g ) ∗ e = ( a ∗ b + c ∗ d ) ∗ e \begin{aligned} f&= a*b\\ g&=c*d\\ h&=f+g\\ &=a*b+c*d\\ i&=h*e\\ &=(f+g)*e\\ &=(a*b+c*d)*e \end{aligned} fghi=a∗b=c∗d=f+g=a∗b+c∗d=h∗e=(f+g)∗e=(a∗b+c∗d)∗e
2.3 变量导数求解
-
i- 最后一层的导数,初始化为
1
- 最后一层的导数,初始化为
-
e
∂ i ∂ e = ∂ i ∂ i ∗ ∂ i ∂ e = ∂ i ∂ i ∗ ∂ h ∗ e ∂ e = 1 ∗ h = a ∗ b + c ∗ d = 2 ∗ 100 + 150 ∗ 3 = 650 \begin{aligned} \frac{\partial i}{\partial e}&= \frac{\partial i}{\partial i}*\frac{\partial i}{\partial e}\\ &=\frac{\partial i}{\partial i}*\frac{\partial h*e}{\partial e}\\ &=1*h\\ &=a*b+c*d\\ &=2*100+150*3\\ &=650 \end{aligned} ∂e∂i=∂i∂i∗∂e∂i=∂i∂i∗∂e∂h∗e=1∗h=a∗b+c∗d=2∗100+150∗3=650 -
h
∂ i ∂ h = ∂ i ∂ i ∗ ∂ i ∂ h = ∂ i ∂ i ∗ ∂ h ∗ e ∂ h = 1 ∗ e = 1.1 \begin{aligned} \frac{\partial i}{\partial h}&= \frac{\partial i}{\partial i}*\frac{\partial i}{\partial h}\\ &=\frac{\partial i}{\partial i}*\frac{\partial h*e}{\partial h}\\ &=1*e\\ &=1.1 \end{aligned} ∂h∂i=∂i∂i∗∂h∂i=∂i∂i∗∂h∂h∗e=1∗e=1.1 -
f和g- 因为 h = f + g h=f+g h=f+g,所以反向传播时,相加的位置,直接将导数传过去即可
- 所以
f和g的导数都为1.1
-
a
∂ f ∂ a = ∂ f ∂ f ∗ ∂ a ∗ b ∂ a = 1.1 ∗ b = 1.1 ∗ 100 = 110 \begin{aligned} \frac{\partial f}{\partial a}&= \frac{\partial f}{\partial f}* \frac{\partial a*b}{\partial a}\\ &=1.1*b\\ &=1.1*100\\ &=110 \end{aligned} ∂a∂f=∂f∂f∗∂a∂a∗b=1.1∗b=1.1∗100=110 -
b
∂ f ∂ b = ∂ f ∂ f ∗ ∂ f ∂ b = 1.1 ∗ ∂ a ∗ b ∂ b = 1.1 ∗ a = 1.1 ∗ 2 = 2.2 \begin{aligned} \frac{\partial f}{\partial b}&= \frac{\partial f}{\partial f}* \frac{\partial f}{\partial b}\\ &=1.1* \frac{\partial a*b}{\partial b}\\ &=1.1*a\\ &=1.1*2\\ &=2.2 \end{aligned} ∂b∂f=∂f∂f∗∂b∂f=1.1∗∂b∂a∗b=1.1∗a=1.1∗2=2.2 -
c
∂ g ∂ c = ∂ g ∂ g ∗ ∂ g ∂ c = 1.1 ∗ ∂ c ∗ d ∂ c = 1.1 ∗ d = 1.1 ∗ 3 = 3.3 \begin{aligned} \frac{\partial g}{\partial c}&= \frac{\partial g}{\partial g}* \frac{\partial g}{\partial c}\\ &=1.1* \frac{\partial c*d}{\partial c}\\ &=1.1*d\\ &=1.1*3\\ &=3.3 \end{aligned} ∂c∂g=∂g∂g∗∂c∂g=1.1∗∂c∂c∗d=1.1∗d=1.1∗3=3.3 -
d
∂ g ∂ d = ∂ g ∂ g ∗ ∂ g ∂ d = 1.1 ∗ ∂ c ∗ d ∂ d = 1.1 ∗ c = 1.1 ∗ 150 = 165 \begin{aligned} \frac{\partial g}{\partial d}&= \frac{\partial g}{\partial g}* \frac{\partial g}{\partial d}\\ &=1.1* \frac{\partial c*d}{\partial d}\\ &=1.1*c\\ &=1.1*150\\ &=165 \end{aligned} ∂d∂g=∂g∂g∗∂d∂g=1.1∗∂d∂c∗d=1.1∗c=1.1∗150=165
3. 代码实现
3.1 参数对应
| 参数 | 代码参数 |
|---|---|
a | dapple_num |
b | dapple |
c | dorange |
d | dorange_num |
e | dall_price |
f | dapple_price |
g | dorange_price |
h | dall_price |
i | dprice |
3.2 代码实现
- 相关代码
# 乘法类 class MulLayer: def __init__(self): self.x = None self.y = None def forward(self, x, y): """ :param x: 价格 :param y: 数量 或 税 :return: 总价 """ self.x = x self.y = y out = x * y return out def backward(self, dout): dx = dout * self.y dy = dout * self.x return dx, dy class AddLayer: def __init__(self): pass def forward(self, x, y): """ 价格相加 :param x: 苹果总价 :param y: 句子总价 :return: 总价 """ out = x + y return out def backward(self, dout): """ 相加的求导直接传递,相当于乘以1 :param dout: 导数 :return: """ dx = dout * 1 dy = dout * 1 return dx, dy if __name__ == '__main__': apple,apple_num = 100,2 orange,orange_num = 150,3 tax = 1.1 # 实例化类 layer mul_apple_layer = MulLayer() # 计算苹果的价格 mul_orange_layer = MulLayer() # 计算橘子的价格 add_apple_orange_layer = AddLayer() # 价格相加 mul_tax_layer = MulLayer() # 计算税后价格 # 前向传播 forward apple_price = mul_apple_layer.forward(apple, apple_num) # 苹果价格*苹果数量 orange_price = mul_orange_layer.forward(orange, orange_num) # 橘子价格*橘子数量 all_price = add_apple_orange_layer.forward(apple_price, orange_price) # 苹果总价+句子总价 price = mul_tax_layer.forward(all_price, tax) # 计算税后价格 # 反向传播 backward dprice = 1 dall_price, dtax = mul_tax_layer.backward(dprice) dapple_price, dorange_price = add_apple_orange_layer.backward(dall_price) dapple, dapple_num = mul_apple_layer.backward(dapple_price) dorange, dorange_num = mul_orange_layer.backward(dorange_price) # 总价 print("price:", int(price)) print("dprice:", dprice) print("dtax:", dtax) print("dall_price:", dall_price) # 苹果 print("dapple_price:", dapple_price) print("dapple_num:", int(dapple_num)) print("dapple:", dapple) # 橘子 print("dorange_price:", dorange_price) print("dorange_num:", int(dorange_num)) print("dorange:", dorange) - 结果