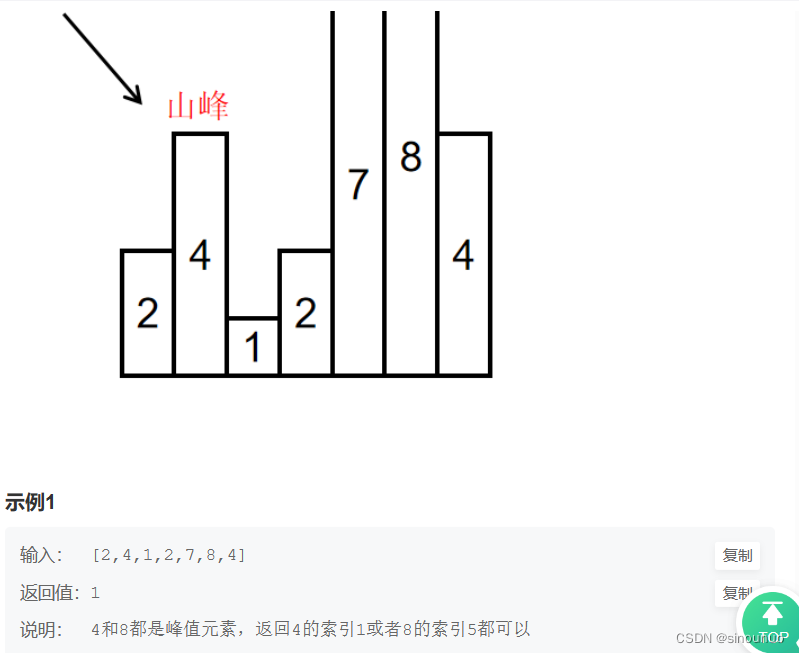
思路:将数组排序,峰值肯定是比较大的那些数,排序后,从大到小,依次看该值是否比左右大,如果是,就返回该值为峰值。
import random
class Solution:
def paixu(self,nums):
if len(nums) <= 1:
return nums
p = random.choice(nums)
left = self.paixu([i for i in nums if i < p])
right = self.paixu([i for i in nums if i > p])
same = [i for i in nums if i == p]
return right+same+left
def findPeakElement(self , nums: List[int]):
num = self.paixu(nums)
nums.insert(0,-2**31-1)
nums.append(-2**31-1) #为了计算方便
for i in num:
if nums[nums.index(i) - 1] < i and nums[nums.index(i) + 1] < i:
return nums.index(i)-1 #因为加了一个头结点,所以索引都增加了1
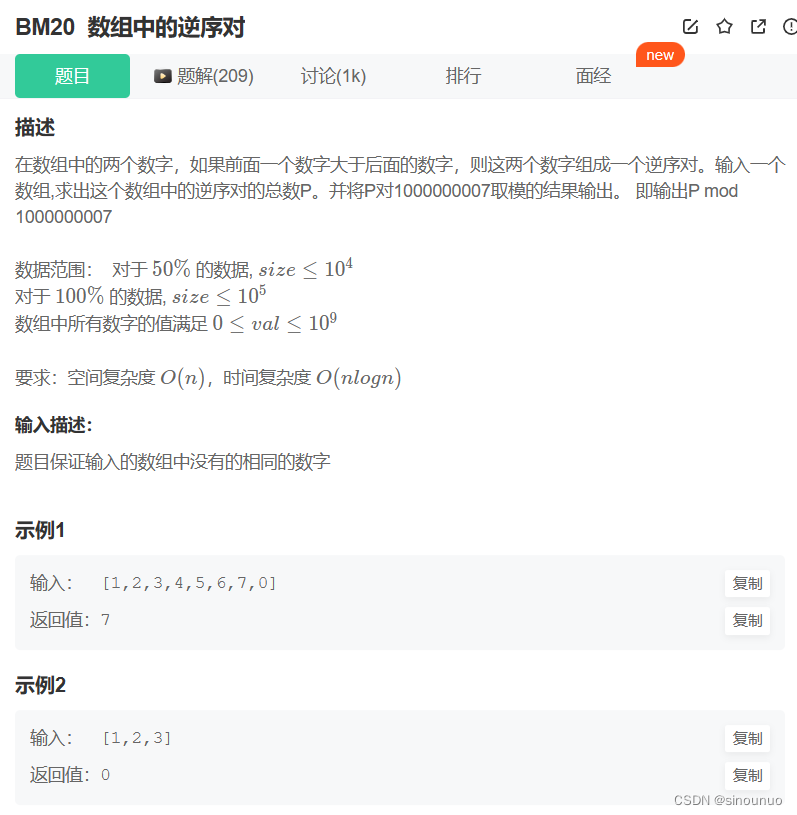
思路:用快排的方式,先找到基准num[0],然后遍历后续的数字,如果比基准大就放到big中,如果比基准小,放到small中。并且计算此时的逆序对,如果当前值小于基准,那么逆序对的个数就是len(big)+1,如果当前值不小于基准,那逆序对个数就是len(big)。递归big和small,返回答案。
class Solution:
def merge(self,num):
if len(num) <= 1: #循环截止条件
return 0
big = []
small = []
p = num[0] #基准
res = 0 #答案
for i in num[1:]:
if i > p:
big.append(i)
else:
small.append(i)
res += len(big) + 1 if p > i else len(big)
return res+self.merge(big)+self.merge(small)
def InversePairs(self , nums: List[int]) -> int:
return self.merge(nums) % 1000000007

思路,二分。旋转之后,数组的最小值一定是乱序的那个点,旋转之后将数组分为两段升序的子数组。如果mid的值大于右边界,那最小值一定在[mid+1,right],如果mid小于右边界,那最小值在[left,mid],如果mid==right,那就不确定在哪个边界,缩小右边界的范围再继续找 right -= 1。
class Solution:
def minNumberInRotateArray(self , nums: List[int]) -> int:
if len(nums) == 1:
return nums[0]
left = 0
right = len(nums) - 1
while left < right:
mid = (left+right) // 2
if nums[right] < nums[mid]:
left = mid + 1
elif nums[right] > nums[mid]:
right = mid
else:
right -= 1
return nums[left]
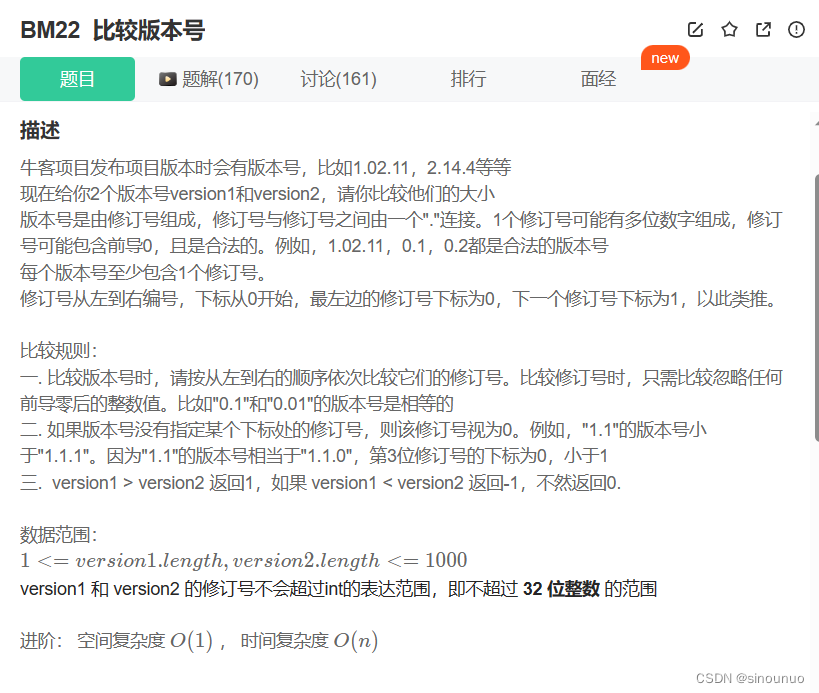
思路:将版本号转成list,补齐长度(补0),然后遍历V1,如果当前值比V2大就返回1,比V2小就返回-1,最后比较完也没有中途退出的话,就返回0.
class Solution:
def compare(self , version1: str, version2: str) -> int:
v1 = list(map(int,version1.split('.'))) #转list
v2 = list(map(int,version2.split('.')))
while len(v1) < len(v2): #补齐
v1.append(0)
while len(v1) > len(v2):
v2.append(0)
for i in range(len(v1)):
if v1[i] < v2[i]:
return -1
elif v1[i] > v2[i]:
return 1
return 0
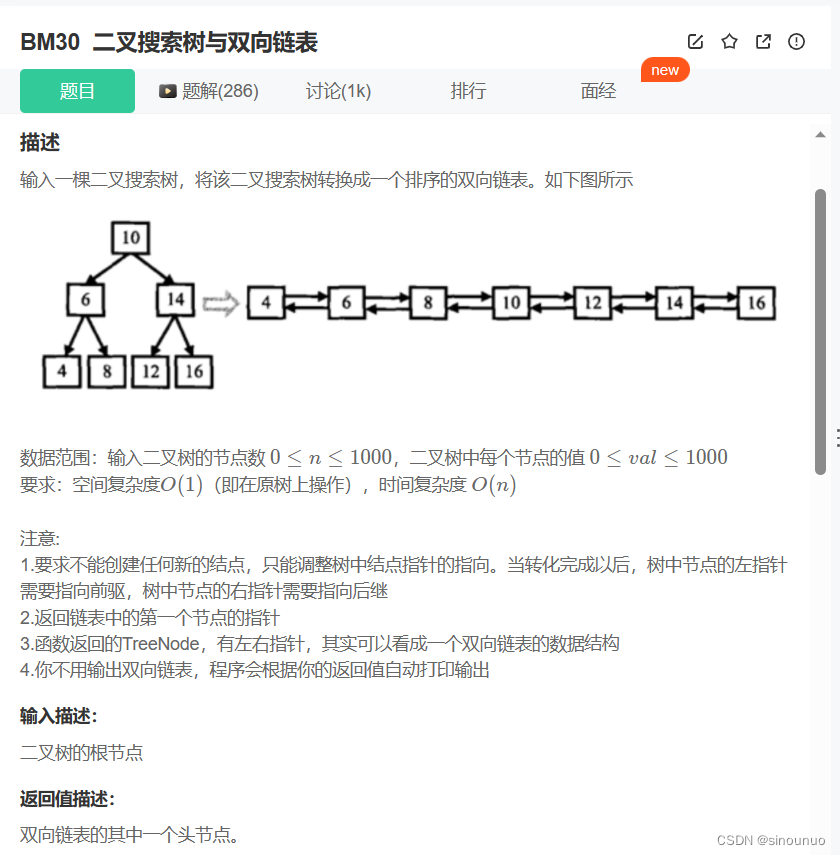
思路:二叉搜索树的中序遍历是个升序序列,所以要中序遍历,在遍历中改变节点。用两个指针,head和pre来指向头结点和前一个节点,初始值为空。当head和pre都是空时,走到了最左边,将head和pre指向该节点。如果不是空,修改pre的右指针指向当前节点,当前节点的左指针指向pre,pre指向当前节点。最后再进行右边的遍历。
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution:
def Convert(self , pRootOfTree ):
head = None
pre = None
if not pRootOfTree:
return head
def vin(node):
if node is None:
return
vin(node.left)
nonlocal head,pre
if not pre:
head = node #如果当前没有pre,就指向当前节点
pre = node
else:
pre.right = node #否则修改节点的指针
node.left = pre
pre = node
vin(node.right)
vin(pRootOfTree)
return head
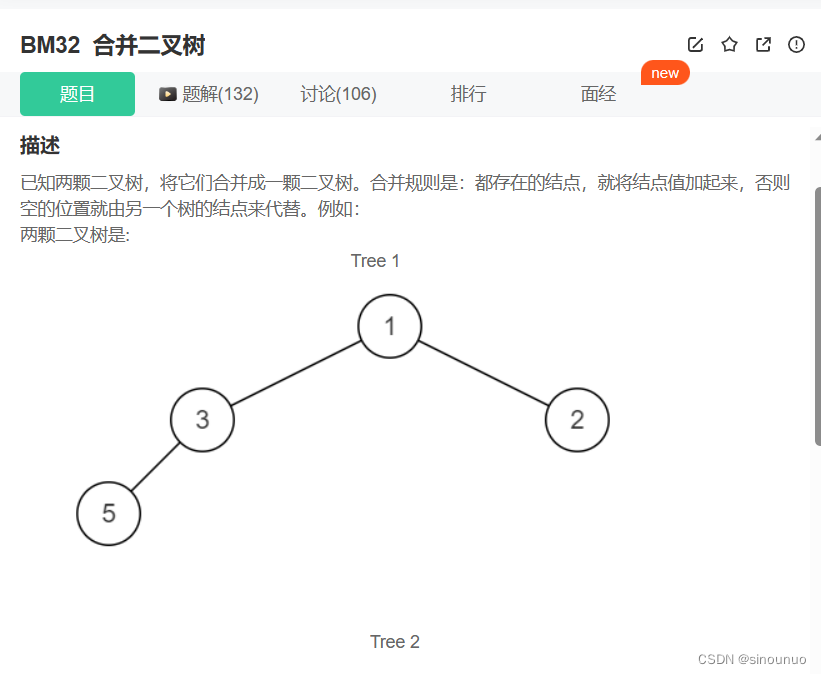
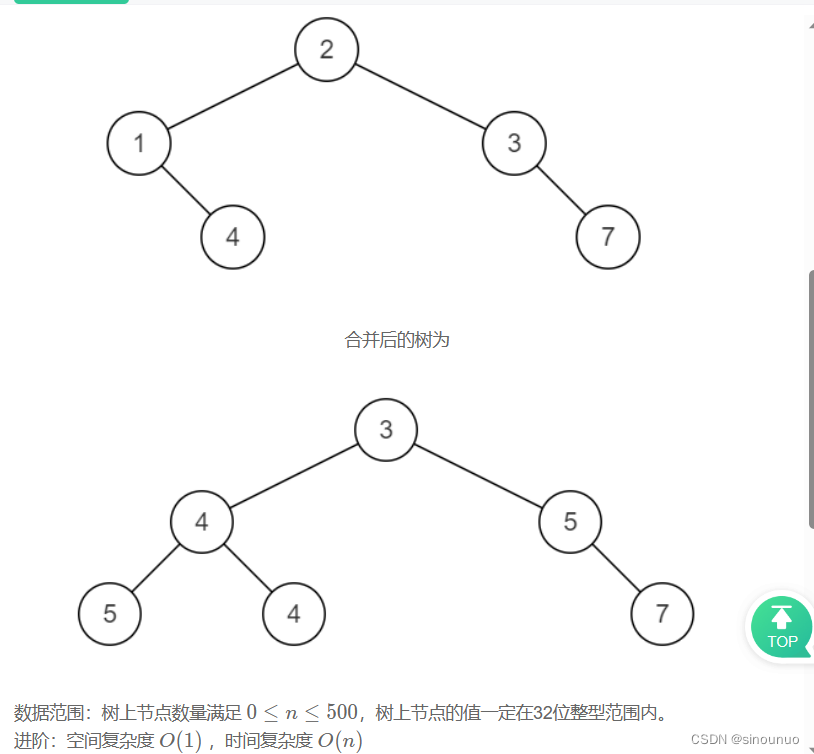
思路:利用前序遍历,每次新建一个节点,如果两个节点都在,就计算和为当前节点值,然后当前节点的左子树等于遍历两个左子树的结果,右子树等于遍历两个右子树的结果。
class Solution:
def mergeTrees(self , t1: TreeNode, t2: TreeNode) -> TreeNode:
if t1 is None:
return t2
if t2 is None:
return t1
head = TreeNode(t1.val+t2.val)
head.left = self.mergeTrees(t1.left,t2.left)
head.right = self.mergeTrees(t1.right,t2.right)
return head
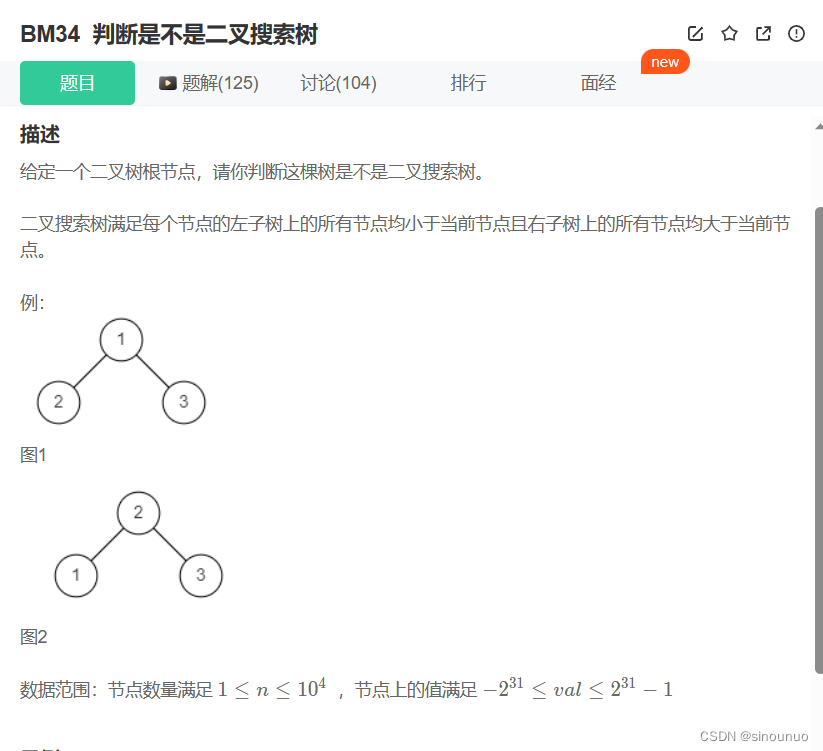
思路一:中序遍历然后将遍历结果保存到num1中,给num1排序到num2,如果是二叉搜索树,那么num2==num1
class Solution:
def isValidBST(self , root: TreeNode) -> bool:
num1 = []
def dfs(root):
if root is None:
return
dfs(root.left)
num1.append(root.val)
dfs(root.right)
dfs(root)
num2 = sorted(num1)
return num1 == num2
思路二:递归左右子树,判断当前节点的值是否符合左右边界。然后递归左子树,修改右边界为root.val,递归右子树,修改左边界为root.val。
class Solution:
def isValidBST(self , root: TreeNode) -> bool:
def dfs(root,l,r):
if root is None:
return True
if root.val < l or root.val > r:
return False
return dfs(root.left,l,root.val) and dfs(root.right,root.val,r)
return dfs(root,-2**31-1,2**31)
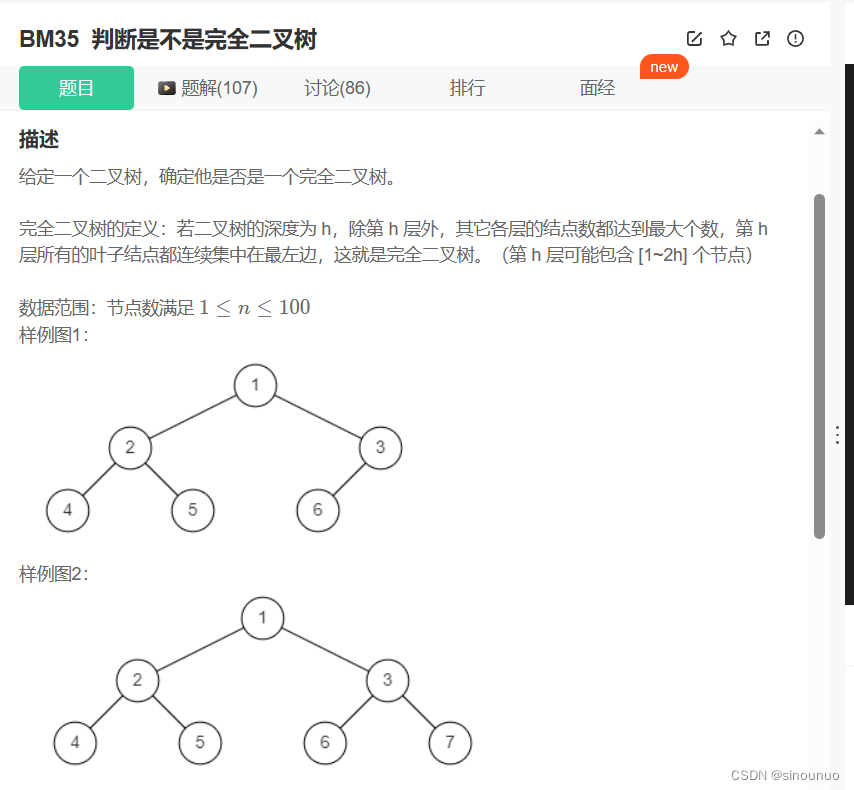
思路:中序遍历,如果当前节点是空,那就已经到了最后一层,将flag置为True,如果在空节点之后又遇到了不为空的节点,那就返回False。加入左右子树的时候,不需要判空。
import collections
class Solution:
def isCompleteTree(self , root: TreeNode) -> bool:
if root is None:
return True
q = collections.deque([root])
flag = False
while q:
for i in range(len(q)):
node = q.popleft()
if not node: #第一次遇到空节点,说明已经到了最后一层,后续不可能再遇到空节点了
flag = True
else:
if flag: #如果之前遇到过空节点,此时又不是空节点,那就不是完全二叉树
return False
q.append(node.left)
q.append(node.right)
return True
思路:如果当前为空,返回0,递归左子树,如果结果是-1,就返回-1,再继续递归右子树,如果结果是-1或者abs(l-r)>1,就返回-1.其余正常情况,返回当前的树高度max(r,l)+1
class Solution:
def IsBalanced_Solution(self , pRoot: TreeNode) -> bool:
def dfs(root):
if root is None:
return 0
l = dfs(root.left)
if l == -1:
return -1
r = dfs(root.right)
if r == -1 or abs(r-l) > 1:
return -1
return max(l,r) + 1
return dfs(pRoot) != -1
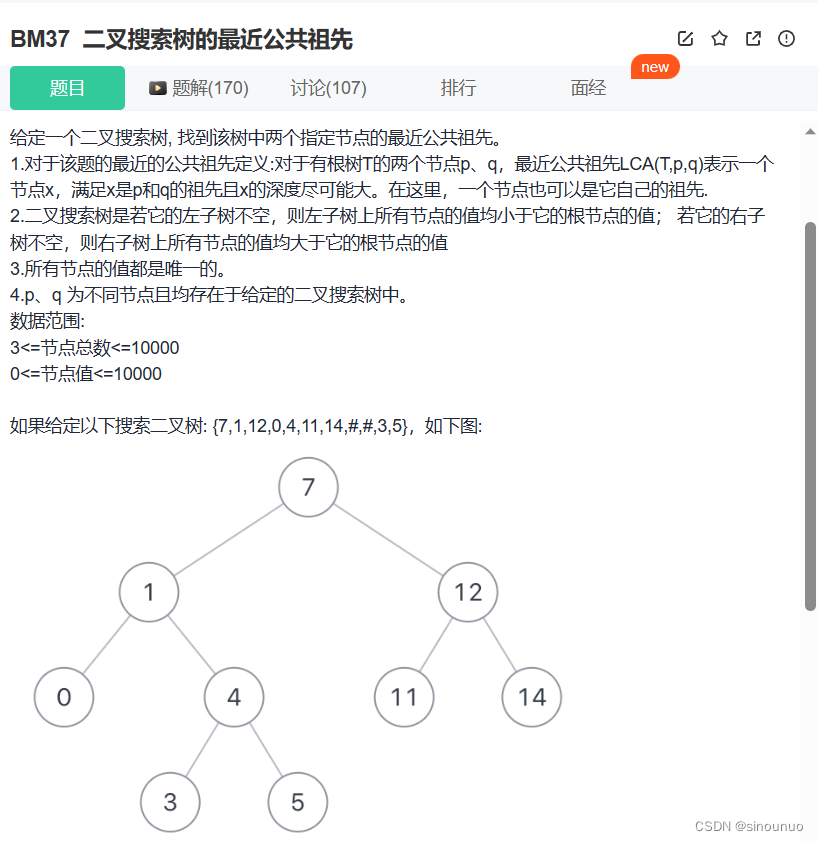
思路:如果p、q在分别在左右子树,那么p、q的最近公共祖先就是当前节点,如果p、q都在右子树,就去右子树递归。如果p、q都在左子树,就去左子树递归。根据二叉搜索树的性质判断p、q所在的子树。
class Solution:
def f(self,node,p,q):
x = node.val
if x < p and x < q:
return self.f(node.right,p,q)
if x > p and x > q:
return self.f(node.left,p,q)
return node
def lowestCommonAncestor(self , root: TreeNode, p: int, q: int) -> int:
return self.f(root,p,q).val
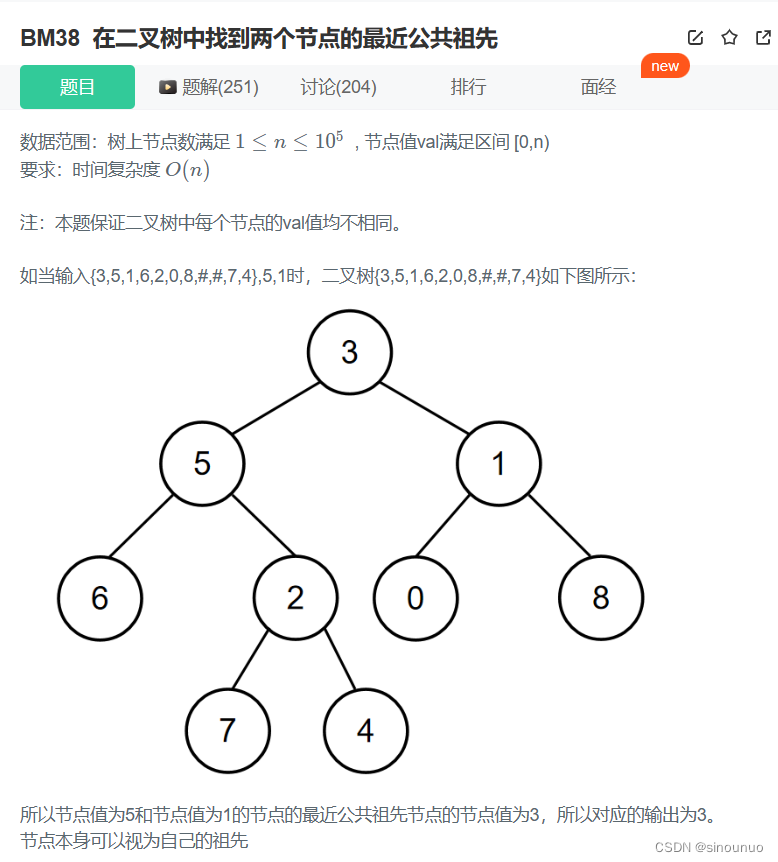
思路:当前节点为空或者当前节点就是p,q就返回当前节点。递归左子树和右子树,如果左右子树都有递归结果,那当前节点就是祖先,如果只有左子树有递归结果,那祖先就是左子树的递归结果。否则就是右子树的递归结果。
class Solution:
def lowestCommonAncestor(self , root: TreeNode, o1: int, o2: int) -> int:
def dfs(root,p,q):
if root is None or root.val == p or root.val == q:
return root
l = dfs(root.left,p,q)
r = dfs(root.right,p,q)
if l and r:
return root
if l:
return l
if r:
return r
return dfs(root,o1,o2).val
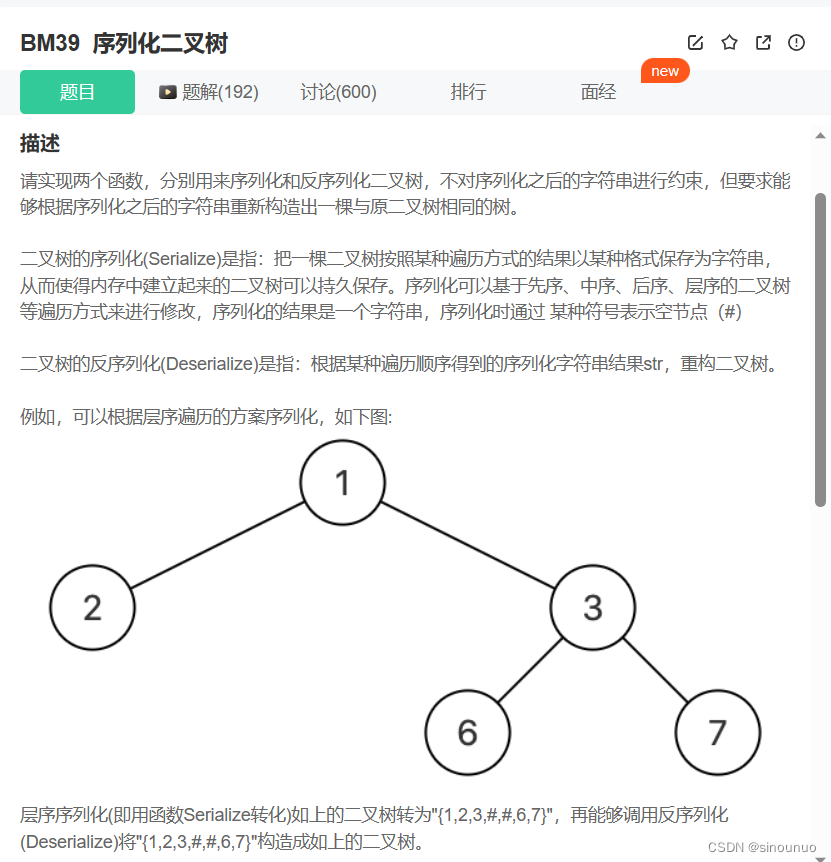
思路:序列化的时候,用层序遍历,如果当前节点不空就将当前值保存并让左右子树入队(不判空),如果为空,就保存为'#'。反序列化的时候,将数据转化为数组。然后遍历数组,先将头结点入队,然后取数组中的两个数,如果当前值不是'#',就创建新节点,连接到队中的节点上,每次移动两个数。
import collections
class Solution:
def Serialize(self, root):
if root is None:
return ''
q = collections.deque([root])
s = []
while q:
for _ in range(len(q)):
node = q.popleft()
if node:
s.append(str(node.val))
q.append(node.left)
q.append(node.right)
else:
s.append('#')
a = ','.join(s)
return a
def Deserialize(self, s):
if len(s) == 0:
return None
tree = s.split(',')
root = TreeNode(int(tree[0])) #创建头结点
q = collections.deque([root]) #头结点入队
i = 1
while i < len(tree)-1:
node = q.popleft()
a,b = tree[i],tree[i+1]
if a != '#':
node.left = TreeNode(int(a))
q.append(node.left)
if b != '#':
node.right = TreeNode(int(b))
q.append(node.right)
i += 2
return root

思路:从前序中找根,然后构建当前节点,从中序中找到左右子树的分界点,然后分别递归左右子树为当前根节点的左右子树。如果前序长度为空,就返回None,否则返回当前节点root。
class Solution:
def reConstructBinaryTree(self , preOrder: List[int], vinOrder: List[int]) -> TreeNode:
if len(preOrder) == 0:
return None
root = TreeNode(preOrder[0])
index = vinOrder.index(preOrder[0])
root.left = self.reConstructBinaryTree(preOrder[1:index+1],vinOrder[:index])
root.right = self.reConstructBinaryTree(preOrder[index+1:],vinOrder[index+1:])
return root

思路:先复原二叉树,然后考虑二叉树的右视图,用ans来存右视图,前序遍历,并且先遍历右子树,再遍历左子树。如果当前深度和ans的长度相同,就保存当前节点。深度和root一起递归,深度每次递归时再加1.
class Solution:
def tree(self,preOrder,inOrder):
if len(preOrder) == 0:
return None
root = TreeNode(preOrder[0])
index = inOrder.index(preOrder[0])
root.left = self.tree(preOrder[1:index+1],inOrder[:index])
root.right = self.tree(preOrder[index+1:],inOrder[index+1:])
return root
def solve(self , preOrder: List[int], inOrder: List[int]) -> List[int]:
root = self.tree(preOrder,inOrder)
ans = []
def dfs(root,h):
if root is None:
return
if h == len(ans):
ans.append(root.val)
dfs(root.right,h+1)
dfs(root.left,h+1)
dfs(root,0)
return ans
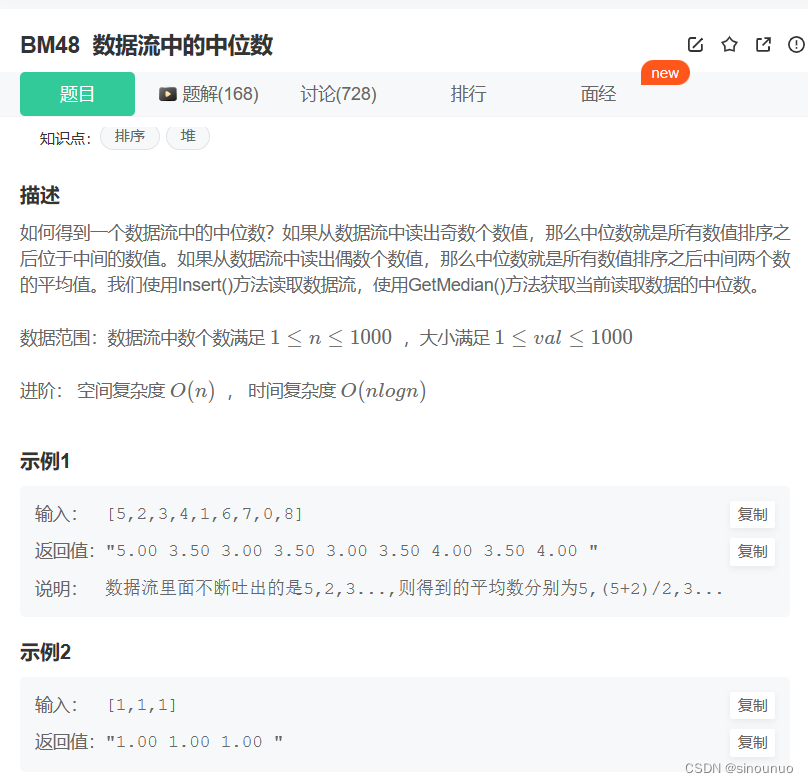
思路:插入排序,如果数组是空,就先插入,如果数组不空就遍历数组,找到比该值大的位置,然后插入。如果遍历完之后依旧没有插入,说明最后一个值小于该值,在最后插入。
class Solution:
def __init__(self) -> None:
self.stack = []
def Insert(self, num):
if len(self.stack) == 0:
self.stack.append(num)
else:
for i in range(len(self.stack)):
if self.stack[i] >= num:
self.stack.insert(i,num)
break
if self.stack[-1] < num:
self.stack.append(num)
def GetMedian(self):
n = len(self.stack)
if n % 2 == 1:
return float(self.stack[n//2])
else:
return (self.stack[n//2-1]+self.stack[n//2])/2.0

思路用哈希表,建立哈希表,最后对哈希表进行排序。按照字典和出现次数排序输出
class Solution:
def FindNumsAppearOnce(self , nums: List[int]) -> List[int]:
d = dict()
for i in nums:
if i not in d:
d[i] = 1
else:
d[i] += 1
nums = sorted(d,key = lambda i:(d[i],i))
return nums[:2]

import collections
class Solution:
def minNumberDisappeared(self , nums: List[int]) -> int:
d = collections.Counter(nums) #用哈希表来快速定位数据
m = len(nums) #长度是m的数组,如果[1,m]么有出现过,那缺失的是m+1,否则缺失的是[1,m]中的数
for i in range(1,m):
if i not in d:
return i
return m+1
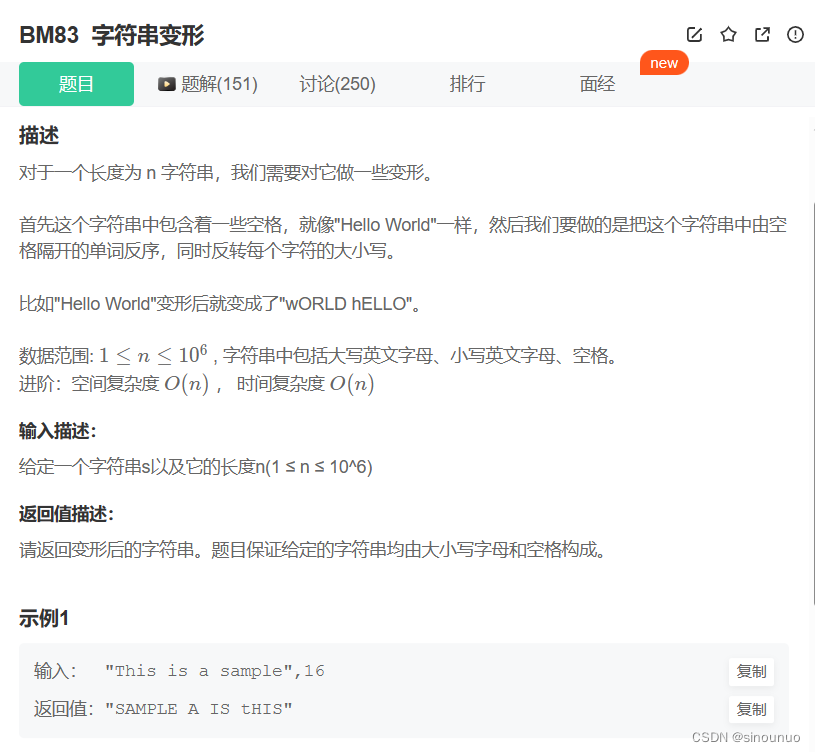
思路:先按照空格分割字符串,然后将其倒序,遍历字符串,如果当前是大写就转换成小写,遍历完一个单词后存入ans中。最后将ans拼接空格输出。
class Solution:
def trans(self , s: str, n: int) -> str:
res = s.split(' ')[::-1]
i = 0
ans = []
while i < len(res):
a = ''
for j in range(len(res[i])):
if res[i][j].isupper():
a += res[i][j].lower()
elif res[i][j].islower():
a += res[i][j].upper()
ans.append(a)
i += 1
return ' '.join(ans)
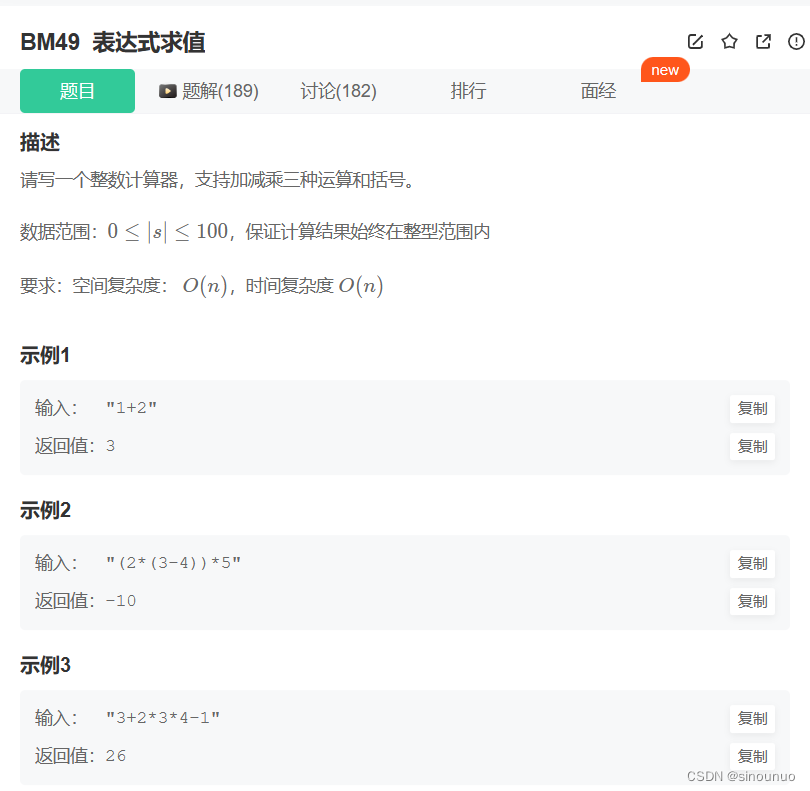
思路:使用栈来存储当前计算的结果,默认是+,每次修改了符号之后,就将当前计算结果重新append进栈中,最后将栈中数据相加。
class Solution:
def solve(self , s: str) -> int:
stack_data = [] #存数据
ans = 0 #存答案
i = 0 #遍历下标
data = 0 #出现过的数字
sign = '+' #当前的符号
while i < len(s):
if s[i] == '(': #将括号视为子问题递归
start = i
end = i+1
while end < len(s) and s[start:end].count('(') != s[start:end].count(')'): #将括号中的内容摘出做递归
end += 1
data = self.solve(s[start+1:end-1])
i = end - 1 #可能到end就是最后一个下标了,但是数据可能还没加入栈,所以退回一个
continue
elif s[i] == ' ': #空格判断
i += 1
continue
if '0' <= s[i] <= '9':
data = data*10 + ord(s[i]) - ord('0') #数字
if not '0' <= s[i] <= '9' or i == len(s) - 1: #如果当前不是数字或者是最后一行
if sign == '+':
stack_data.append(data)
elif sign == '-':
stack_data.append(-data)
elif sign == '*':
stack_data.append(stack_data.pop()*data)
elif sign == '/':
stack_data.append(stack_data.pop()/data)
data = 0 #恢复数据
sign = s[i] #标记当前的符号
i += 1
while stack_data:
ans += stack_data.pop()
return ans