题目描述
我们现在要利用 m m m 台机器加工 n n n 个工件,每个工件都有 m m m 道工序,每道工序都在不同的指定的机器上完成。每个工件的每道工序都有指定的加工时间。
每个工件的每个工序称为一个操作,我们用记号 j-k 表示一个操作,其中
j
j
j 为
1
1
1 到
n
n
n 中的某个数字,为工件号;
k
k
k 为
1
1
1 到
m
m
m 中的某个数字,为工序号,例如 2-4 表示第
2
2
2 个工件第
4
4
4 道工序的这个操作。在本题中,我们还给定对于各操作的一个安排顺序。
例如,当
n
=
3
,
m
=
2
n=3,m=2
n=3,m=2 时,1-1,1-2,2-1,3-1,3-2,2-2 就是一个给定的安排顺序,即先安排第
1
1
1 个工件的第
1
1
1 个工序,再安排第
1
1
1 个工件的第
2
2
2 个工序,然后再安排第
2
2
2 个工件的第
1
1
1 个工序,等等。
一方面,每个操作的安排都要满足以下的两个约束条件。
-
对同一个工件,每道工序必须在它前面的工序完成后才能开始;
-
同一时刻每一台机器至多只能加工一个工件。
另一方面,在安排后面的操作时,不能改动前面已安排的操作的工作状态。
由于同一工件都是按工序的顺序安排的,因此,只按原顺序给出工件号,仍可得到同样的安排顺序,于是,在输入数据中,我们将这个安排顺序简写为 1 1 2 3 3 2。
还要注意,“安排顺序”只要求按照给定的顺序安排每个操作。不一定是各机器上的实际操作顺序。在具体实施时,有可能排在后面的某个操作比前面的某个操作先完成。
例如,取 n = 3 , m = 2 n=3,m=2 n=3,m=2,已知数据如下(机器号/加工时间):
| 工件号 | 工序 1 1 1 | 工序 2 2 2 |
|---|---|---|
| 1 1 1 | 1 / 3 1/3 1/3 | 2 / 2 2/2 2/2 |
| 2 2 2 | 1 / 2 1/2 1/2 | 2 / 5 2/5 2/5 |
| 3 3 3 | 2 / 2 2/2 2/2 | 1 / 4 1/4 1/4 |
则对于安排顺序 1 1 2 3 3 2,下图中的两个实施方案都是正确的。但所需要的总时间分别是
10
10
10 与
12
12
12。
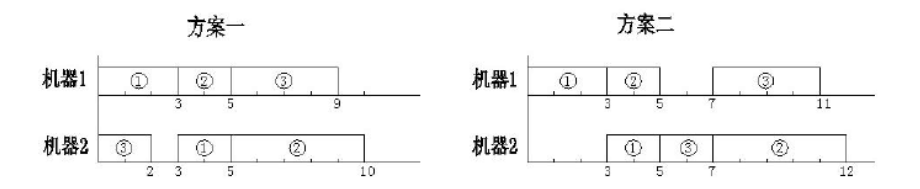
当一个操作插入到某台机器的某个空档时(机器上最后的尚未安排操作的部分也可以看作一个空档),可以靠前插入,也可以靠后或居中插入。为了使问题简单一些,我们约定:在保证约束条件( 1 1 1)( 2 2 2)的条件下,尽量靠前插入。并且,我们还约定,如果有多个空档可以插入,就在保证约束条件( 1 1 1)( 2 2 2)的条件下,插入到最前面的一个空档。于是,在这些约定下,上例中的方案一是正确的,而方案二是不正确的。
显然,在这些约定下,对于给定的安排顺序,符合该安排顺序的实施方案是唯一的,请你计算出该方案完成全部任务所需的总时间。
输入格式
第
1
1
1 行为两个正整数
m
m
m,
n
n
n,用一个空格隔开,
(其中
m
(
<
20
)
m(<20)
m(<20) 表示机器数,
n
(
<
20
)
n(<20)
n(<20) 表示工件数)
第 2 2 2 行: m × n m \times n m×n 个用空格隔开的数,为给定的安排顺序。
接下来的 2 n 2n 2n 行,每行都是用空格隔开的 m m m 个正整数,每个数不超过 20 20 20。
其中前 n n n 行依次表示每个工件的每个工序所使用的机器号,第 1 1 1 个数为第 1 1 1 个工序的机器号,第 2 2 2 个数为第 2 2 2 个工序机器号,等等。
后 n n n 行依次表示每个工件的每个工序的加工时间。
可以保证,以上各数据都是正确的,不必检验。
输出格式
1 1 1 个正整数,为最少的加工时间。
样例 #1
样例输入 #1
2 3
1 1 2 3 3 2
1 2
1 2
2 1
3 2
2 5
2 4
样例输出 #1
10
提示
NOIP 2006 提高组 第三题
1.题目分析
第一行输入M,N分别代表机器数和工件数。
第二行输入每一个工件数的加工顺序。
后面的第一个n行代表,每一个工件,处理对应的顺序的工序,需要的机械号数,
第二个n行代表,上面第一个n行工件,使用指定机械流水线,处理指定工序所需要花费的时间。
求机器流水线处理完所有工件数需要花费的时间。
这道题确实逻辑挺绕的,这里做几点说明:
- 一个工件需要若干次的加工才算完成,而这里的加工次数是和机械流水线的数量是一致的。
- 后面分别输入的N行M列的两次数据是为了得到题中的表:即工件号,工序号以及机械号和单次所需要花费时间的关系。
- 而第二行中的加工顺序:就是根据表格的对应关系,输入指定的工件号,按照流水线:工序1,2,3…n,根据机械号选取对应的机械进行加工,并根据其中的时间计算出最长时间的流水线的时长。
2.题目思路
设计一个结构体,存储每一次工序中的机械id,时间开销。
主函数:
定义一个二维数组存储所有的机械流水线的时间轴占用情况,1为占用,0为空闲,每一行代表一台机械所有的流水线。
定义一个一维数组存储工件的加工顺序。
定义一个上述的二维结构体数组,用于存储工件号和机械号以及工序号和时间开销的对应关系图。
定义一个一维数组用于存储每一个工件的加工进度,索引代表工件号,值代表加工的次数。
定义一个一维数组last_time用于存储每一个工件的某一次工序结束后的时间点,索引代表工件号,值代表该工件最后一次加工的时间点。
定义一个整数代表最终的时间开销。
依次读入数据,
循环遍历加工顺序,读取当前加工的工件,当前加工的工件的工序数:即第几次加工,
获取当前机械数id以及当前所需要的时间cost,
定义一个临时变量判断某个时间段是否可加工,
从存储结束时间的数组中一个索引index,即前一个工件后加工后的时间点,如果是第一个工件开始加工时,开始时间都设为零。
进入内部while循环,遍历当前机械id对应的流水线数组的时间点,起始点为index,
按顺序寻找未被占用的时间段,即要出现连续cost个0时,将这些个0覆盖为1,代表占用,
并赋值此次时间点到last_time数组的加工顺序索引处,
同时与最大开销时间进行比较,将较大值赋值给最大时间,然后跳出内循环。
外循环结束后,直接打印最大时间即可。
3.代码演示
#include <iostream>
using namespace std;
//工序图:记录某一件工件在当前机械上某一道工序中需要的加工时间
typedef struct data {
//机械号id
int id;
//加工当前机械上的某一件工件中的一道工序所需要的时间开销
int time;
} process;
int main() {
//所有机器加工的流水线
int line[21][10000] = {0};
//机器数和工件数
int m, n;
cin >> m >> n;
//工件的加工顺序
int order[m * n];
//工序图:二维结构体数组。工件号和机械号以及工序号的对应关系
process processes[21][21];
//记录每一个工件进行到的工序数
int step[21] = {0};
//最终的时间开销
int res = 0;
//记录每一次工序结束后的时间点
int last_time[21] = {0};
//键入加工顺序
for (int i = 0; i < m * n; ++i) {
cin >> order[i];
}
//键入机器号
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
cin >> processes[i][j].id;
}
}
//键入花费的时间
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
cin >> processes[i][j].time;
}
}
//依次读取加工顺序
for (int i = 0; i < m * n; ++i) {
//读取当前加工的工件
int now = order[i] - 1;
//当前加工的工件的工序数:即第几次加工
int num = step[now]++;
//获取当前机械数id
int id = processes[now][num].id;
//获取当前所需要的时间
int cost = processes[now][num].time;
//定义一个临时变量判断某个时间段是否可加工
int point = 0;
//索引
int index;
//前一个工件后加工后的时间点,如果是第一个工件开始加工时,开始时间都设为零
index = last_time[now] + 1;
while (true) {
//从上一次同一产品加工结束的时间点开始
if (line[id][index] == 0) {
//判断当前工件开始加工的时间点
point++;
} else {
//如果当前流水线上机器正在被占用,则重新开始统计可持续加工的时间
point = 0;
}
if (point == cost) {
//如果出现连续的时间,可供当前产品加工则
// 将这段时间标记为占用
for (int j = index - point + 1; j <= index; ++j) {
line[id][j] = 1;
}
//记录最大的产品结束时间点
if (index > res) {
res = index;
}
//记录当前产品(产品之间的工序互不关联)的时间点
last_time[now] = index;
break;
}
index++;
}
}
cout << res;
return 0;
}





![java八股文面试[JVM]——双亲委派模型](https://img-blog.csdnimg.cn/fb7bfbb2eb604b7bb4f7e52d2fb5f565.png)