优先级队列—数据结构

news2024/11/20 19:28:28

文章目录

  • 1.堆
    • 1.1概念
    • 1.2性质
    • 1.3存储方式
    • 1.4堆向下调整创建大根堆
    • 1.5堆的插入和删除
    • 1.6
  • 2.PriorityQueue
    • 2.1定义
    • 2.2性质
    • 2.3 PriorityQueue常用接口介绍
    • 2.4方法的使用
    • 2.5对复杂类型的PriorityQueue的使用
  • 3.堆的应用
    • 3.1PriorityQueue的实现
    • 3.2Top-k问题
    • 3.3堆排序
  • 4.经典习题

1.堆

1.1概念

小堆（小根堆）：根结点比左右孩子都大的完全二叉树，左右孩子大小是不确定的
大堆（大根堆）：根结点比左右孩子都小的完全二叉树，左右孩子大小是不确定的

1.2性质

（1）堆是一组集合中所有元素按照完全二叉树的顺序存储方式存储在一个一维数组中
（2）堆是一棵完全二叉树
（3）某个结点的值总是不大于或者不小于父节点的值

1.3存储方式

由于堆是一棵完全二叉树，采用顺序的方式存储，采取层序遍历，是以数组的形式进行存储；非完全二叉树，则不适合使用顺序方式进行存储，因为为了能够还原二叉树，空间中必须要存储空节点，就会导致空间利用率比较低

1.4堆向下调整创建大根堆

（1）已知孩子结点下标i：父亲结点下标为（i - 1）/2
（2）已知父亲结点下标j：左结点下标为2 * j + 1；右孩子结点下标：2 * j + 2

public class TestHeap {
    public int[] elem;
    public int usedSize;
    public TestHeap(){
        this.elem = new int[10];
    }

    //创建一个大根堆
    public void createHeap(int[] array){
        for (int i = 0; i < array.length; i++) {
            this.elem[i] = array[i];
            this.usedSize++;
        }
        for (int parent = (this.usedSize - 1 - 1)/2; parent >= 0; parent--) {
            shiftDown(parent,array.length);
        }
    }

    //向上调整
    public void shiftDown(int parent,int len){
        int child = parent * 2 + 1;
        while (child < len){
            if (child + 1 < len && elem[child] < elem[child + 1]){
                child++;
            }
            if (elem[child] > elem[parent]){
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;
                parent = child;
                child = parent * 2 + 1;
            }else {
                break;
            }
        }
    }
}

（3）向下调整的时间复杂度：最坏的情况是O(logN)
（4）建堆的时间复杂度是：O(N)
在这里插入图片描述

1.5堆的插入和删除

（1）堆的插入总共需要两个步骤：

  1. 先将元素放入到底层空间中(注意：空间不够时需要扩容)
  2. 将最后新插入的节点向上调整，直到满足堆的性质
    （2）堆的删除一定删除的是堆顶元素，需要两个步骤：
  3. 将堆顶元素对堆中最后一个元素交换
  4. 将堆中有效数据个数减少一个
  5. 对堆顶元素进行向下调整
import java.awt.*;
import java.util.Arrays;

public class TestHeap {
    public int[] elem;
    public int usedSize;
    public TestHeap(){
        this.elem = new int[10];
    }

    //向上调整
    public void shiftDown(int parent,int len){
        int child = parent * 2 + 1;
        while (child < len){
            if (child + 1 < len && elem[child] < elem[child + 1]){
                child++;
            }
            if (elem[child] > elem[parent]){
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;
                parent = child;
                child = parent * 2 + 1;
            }else {
                break;
            }
        }
    }

    //添加一个数据到堆中
    public void push(int val){
        if (isFull()){
            this.elem = Arrays.copyOf(this.elem,this.elem.length * 2);
        }
        //把添加的数据放到堆中的最后一个位置
        this.elem[this.usedSize] = val;
        this.usedSize++;
        //向上调整将其变成一个大根堆
        shiftUp(this.usedSize - 1);
    }

    //向上调整
    public void shiftUp(int child){
        int parent = (child - 1) /2;
        while (parent >= 0){
            if (this.elem[parent] < this.elem[child]){
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;
                child = parent;
                parent = (child - 1) / 2;
            }else {
                break;
            }
        }
    }
    //判断堆是否为空
    public boolean isFull(){
        if (this.elem.length == this.usedSize){
            return true;
        }
        return false;
    }

    //出队，删除堆顶元素
    public int remove(){
        if (this.elem.length == 0){
            throw new HeadlessException("堆为空");
        }
        //交换堆顶元素和堆的最后一个元素
        int tmp = this.elem[this.usedSize - 1];
        this.elem[this.usedSize - 1] = this.elem[0];
        this.elem[0] = tmp;
        this.usedSize--;
        shiftDown(0,this.usedSize);
        return tmp;
    }
}

1.6

2.PriorityQueue

2.1定义

  1. 数据结构应该提供了两个最基本的操作，一个是返回最高优先级对象，一个是添加新的对象，这种数据结构就是优先级队列（PriorityQueue）
  2. PriorityQueue底层使用了堆的数据结构
  3. Java集合框架中提供了PriorityQueue和PriorityBlockingQueue两种类型的优先级队列，PriorityQueue是线程不安全的，PriorityBlockingQueue是线程安全的

2.2性质

  1. 使用时必须导入PriorityQueue所在的包，import java.util.PriorityQueue;
  2. PriorityQueue中放置的元素必须要能够比较大小，不能插入无法比较大小的对象，否则会抛出ClassCastException异常
  3. 不能插入null对象，否则会抛出NullPointerException
  4. 没有容量限制，可以插入任意多个元素，其内部可以自动扩容
  5. 插入和删除元素的时间复杂度为O(logN)
  6. PriorityQueue底层使用了堆数据结构
  7. PriorityQueue默认情况下是小堆，也就是每次获取到的元素都是最小的元素

2.3 PriorityQueue常用接口介绍

import java.util.*;
public class TestHeap2 {
    public static void main(String[] args) {
        //创建一个空的优先级队列，默认容量是11（默认是小根堆）
        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
        priorityQueue.offer(311);
        priorityQueue.offer(223);
        System.out.println(priorityQueue);//[223, 311]
        //创建一个初始容量为3的优先级队列（默认是小根堆）
        PriorityQueue<Integer> priorityQueue2 = new PriorityQueue<>(3);
        priorityQueue2.offer(16);
        priorityQueue2.offer(4);
        System.out.println(priorityQueue2);//[4, 16]
        //创建一个大根堆
        PriorityQueue<Integer> priorityQueue1 = new PriorityQueue<>(Collections.reverseOrder());
        priorityQueue1.offer(16);
        priorityQueue1.offer(4);
        System.out.println(priorityQueue1);//[16, 4]
        //创建一个大根堆（
        PriorityQueue<Integer> priorityQueue3 = new PriorityQueue<>(new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2 - o1;
            }
        });
        priorityQueue3.offer(16);
        priorityQueue3.offer(4);
        System.out.println(priorityQueue3);//[16, 4]
    }
}

2.4方法的使用

public class TestHeap2 {
    public static void main(String[] args) {
        //创建一个空的优先级队列，默认容量是11（默认是小根堆）
        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
        priorityQueue.offer(311);//添加元素
        priorityQueue.offer(223);
        System.out.println(priorityQueue);//[223, 311]
        System.out.println(priorityQueue.peek());//获取堆顶元素 233
        priorityQueue.poll();//删除堆顶元素
        System.out.println(priorityQueue);//[311]
        System.out.println(priorityQueue.isEmpty());//false
        System.out.println(priorityQueue.size());//1
    }
}

2.5对复杂类型的PriorityQueue的使用

  1. 实现Comparable接口
import java.util.*;

class Student implements Comparable<Student>{
    public String name;
    public int age;

    public Student(String name, int age) {
        this.name = name;
        this.age = age;
    }

    @Override
    public String toString() {
        return "Student{" +
                "name='" + name + '\'' +
                ", age=" + age +
                '}';
    }

    @Override
    public int compareTo(Student o) {
//        return this.age - o.age;//小堆
        return o.age - this.age;//大堆
    }
}
public class TestHeap2 {
    public static void main(String[] args) {
        PriorityQueue<Student> students = new PriorityQueue<>();
        students.offer(new Student("张三",10));
        students.offer(new Student("李四",19));
        System.out.println(students);
    }
}
  1. 重写比较器
import java.util.*;
class Student{
    public String name;
    public int age;

    public Student(String name, int age) {
        this.name = name;
        this.age = age;
    }

    @Override
    public String toString() {
        return "Student{" +
                "name='" + name + '\'' +
                ", age=" + age +
                '}';
    }
}

/**
 * 重写comparator年龄比较器
 */
class AgeComparator implements Comparator<Student>{
    @Override
    public int compare(Student o1, Student o2) {
//        return o1.age - o2.age;//小堆
        return o2.age - o1.age;//大堆
    }
}
public class TestHeap2 {
    public static void main(String[] args) {
        AgeComparator ageComparator = new AgeComparator();
        PriorityQueue<Student> students = new PriorityQueue<>(ageComparator);
        students.offer(new Student("张三",10));
        students.offer(new Student("李四",19));
        System.out.println(students);
    }
}

3.堆的应用

3.1PriorityQueue的实现

用堆作为底层结构封装优先级队列

3.2Top-k问题

基本思路：

  1. 用数据集合中前K个元素来建堆（前k个最大的元素，则建小堆；前k个最小的元素，则建大堆）
  2. 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素
/**
     * 找前k个最小值
     * @param array
     * @param k
     * @return
     */
    public int[] topK(int[] array,int k){
        //创建一个大堆
        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(k, new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2 - o1;
            }
        });
        //PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(k, Collections.reverseOrder());
        for (int i = 0; i < array.length; i++) {
            if (i < k){
                priorityQueue.offer(array[i]);
            }else {
                if (array[i] < priorityQueue.peek()){
                    priorityQueue.poll();
                    priorityQueue.offer(array[i]);
                }
            }
        }
        int[] tmp = new int[priorityQueue.size()];
        for (int i = 0; i < tmp.length; i++) {
            tmp[i] = priorityQueue.poll();

        }
        return tmp;
    }

3.3堆排序

思路：

  1. 建堆
    升序：建大堆
    降序：建小堆
  2. 利用堆删除思想来进行排序，向上调整进行排序
/**
     * 堆排序
     * @param array
     */
    public static void heapSort(int[] array){
        //创建一个大根堆
        createHeap(array);
        //向下调整进行排序
        int end = array.length - 1;
        while (end > 0){
            swap(array,0,end);
            shiftDown(array,0,end);
            end--;
        }
    }

    /**
     * 创建大根堆
     * @param array
     */
    private static void createHeap(int[] array){
        for (int parent = (array.length - 1- 1)/2;parent >= 0;parent--){
            shiftDown(array,parent,array.length);
        }
    }

    /**
     * 向下调整
     * @param array
     * @param parent
     * @param len
     */
    private static void shiftDown(int[] array,int parent,int len){
        int child = parent * 2 + 1;
        while (child < len){
            if (child + 1 < len && array[child] < array[child + 1]){
                child++;
            }
            if (array[child] > array[parent]){
                swap(array,child,parent);
                parent = child;
                child = parent * 2 + 1;
            }else {
                break;
            }
        }
    }

4.经典习题

1.下列关键字序列为堆的是:(A)
A: 100,60,70,50,32,65
B: 60,70,65,50,32,100
C: 65,100,70,32,50,60
D: 70,65,100,32,50,60
E: 32,50,100,70,65,60
F: 50,100,70,65,60,32
解析：堆只能是小根堆或者大根堆，也就是说他的父亲结点的大小必须全部大于孩子节点（大根堆）或者小于孩子节点（小根堆）

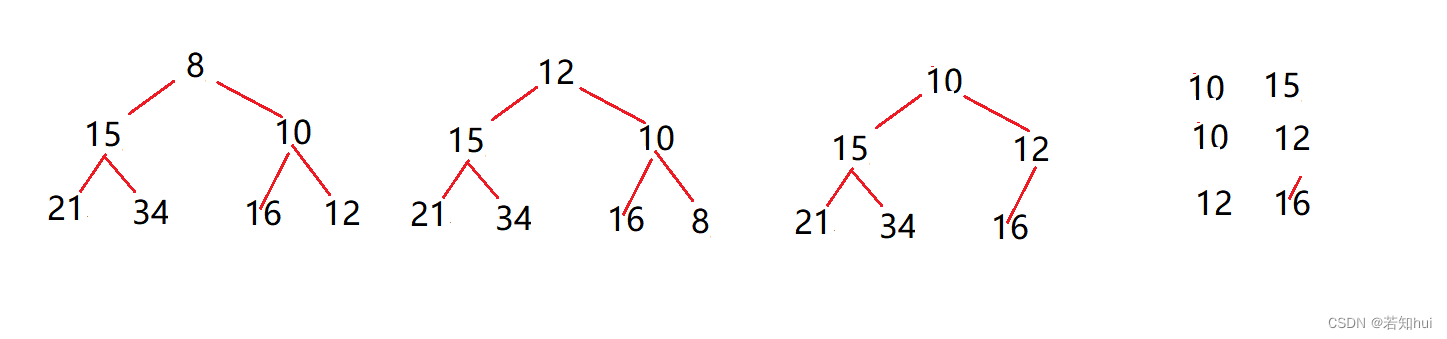
2.已知小根堆为8,15,10,21,34,16,12，删除关键字8之后需重建堆，在此过程中，关键字之间的比较次数是©
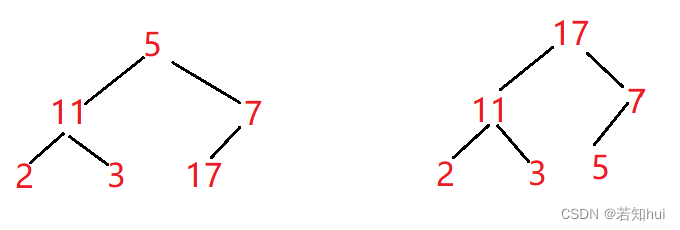
A: 1 B: 2 C: 3 D: 4在这里插入图片描述

3.一组记录排序码为(5 11 7 2 3 17),则利用堆排序方法建立的初始堆为©
A: (11 5 7 2 3 17)
B: (11 5 7 2 17 3)
C: (17 11 7 2 3 5)
D: (17 11 7 5 3 2)
E: (17 7 11 3 5 2)
F: (17 7 11 3 2 5)
解析：堆排需要先建立大根堆
在这里插入图片描述

4.最小堆[0,3,2,5,7,4,6,8],在删除堆顶元素0之后，其结果是©
A: [3，2，5，7，4，6，8]
B: [2，3，5，7，4，6，8]
C: [2，3，4，5，7，8，6]
D: [2，3，4，5，6，7，8]
解析：删除元素是交换根结点和最后一个元素，再进行调整

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/927405.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【校招VIP】专业课考点之死锁检测与恢复

【校招VIP】专业课考点之死锁检测与恢复

考点介绍&#xff1a; 根据不少同学的面试反馈&#xff0c;最近阿里和字节跳动面试时面试官都问到了死锁问题。如字节跳动考察的问题是&#xff1a;什么是线程死锁&#xff1f;死锁如何产生&#xff1f;死锁如何检测与恢复&#xff1f;其产生的原理与对应的解决方案都是重点考察…
阅读更多...
跨境电商服务商哪家靠谱，要怎么选择？

跨境电商服务商哪家靠谱，要怎么选择？

随着全球市场的不断扩大&#xff0c;跨境电商已成为众多企业进军国际贸易的重要途径。然而&#xff0c;跨境电商涉及的法规、市场策略、国际物流等方面的知识相当复杂&#xff0c;因此&#xff0c;寻找一个优质的跨境电商培训中心成为了企业不可或缺的需求。本文将为您介绍如何…
阅读更多...
什么气传导蓝牙耳机好？气传导耳机最新品牌推荐

什么气传导蓝牙耳机好？气传导耳机最新品牌推荐

​传统入耳式耳机佩戴着容易滑落&#xff0c;戴不稳&#xff0c;久戴耳朵酸痛等问题&#xff0c;气传导耳机的出现就避免了这些问题的发生&#xff0c;我来推荐几款市面上热销火爆且使用感不错的气传导耳机给到大家&#xff0c;来看看吧&#xff01; 一、南卡00压开放式耳机&a…
阅读更多...
汉诺塔问题--夏令营

汉诺塔问题--夏令营

题目 tips&#xff1a; 1.本题只用多试几次&#xff0c;由数据推导规律即可 2.汉诺塔问题分析 这里的递归函数是&#xff08;n,a,b,c&#xff09;指n个盘子从a移到c&#xff0c;且凭借b 递归边界是n1 原始思想&#xff1a;要想把n个盘子从a移到c,若n1则直接move a到c n>…
阅读更多...
Web3.0的五大趋势，你是否已经了解？

Web3.0的五大趋势，你是否已经了解？

&#x1f935;‍♂️ 个人主页&#xff1a;艾派森的个人主页 ✍&#x1f3fb;作者简介&#xff1a;Python学习者 &#x1f40b; 希望大家多多支持&#xff0c;我们一起进步&#xff01;&#x1f604; 如果文章对你有帮助的话&#xff0c; 欢迎评论 &#x1f4ac;点赞&#x1f4…
阅读更多...
美格智能亮相elexcon 2023：边缘AI算力，赋能物联网终端创新升级

美格智能亮相elexcon 2023：边缘AI算力，赋能物联网终端创新升级

8月23~25日&#xff0c;elexcon 2023深圳国际电子展在深圳会展中心&#xff08;福田&#xff09;盛大举办。本届展会聚焦“嵌入式与AIoT展”“电源与储能展”“SiP与先进封装展”三大板块&#xff0c;规模达40000㎡&#xff0c;共计600家全球嵌入式产业链厂商齐聚现场&#xff…
阅读更多...
ChatGPT解锁亲子互动新方式，10种方法教你带孩子一起探索AI世界

ChatGPT解锁亲子互动新方式，10种方法教你带孩子一起探索AI世界

与孩子们一起进入AI的世界&#xff0c;点击一下按钮就可以得到你所有问题的答案。 ChatGPT是当下的热门话题&#xff0c;它正在以风暴之势席卷人工智能的世界&#xff01;大多数宝妈和宝爸可能已经听说过它&#xff0c;但有许多人会觉得它与自己日常并无关联。事实上&#xf…
阅读更多...
webuploader分片上传

webuploader分片上传

WebUploader 分片上传的基本原理 切割文件&#xff1a; 当用户选择一个需要上传的文件时&#xff0c;WebUploader 将这个文件切割成固定大小的切片&#xff08;chunks&#xff09;&#xff0c;每个切片的大小由配置参数决定。这些切片通常是二进制数据块&#xff0c;每个切片都…
阅读更多...
使用DPO微调Llama2

使用DPO微调Llama2

简介 基于人类反馈的强化学习 (Reinforcement Learning from Human Feedback&#xff0c;RLHF) 事实上已成为 GPT-4 或 Claude 等 LLM 训练的最后一步&#xff0c;它可以确保语言模型的输出符合人类在闲聊或安全性等方面的期望。然而&#xff0c;它也给 NLP 引入了一些 RL 相关…
阅读更多...
认准这几条Web设计规范，做好Web不在话下！

认准这几条Web设计规范，做好Web不在话下！

在当今数字化的世界中&#xff0c;Web设计的重要性愈发凸显。无论是企业网站、电子商务平台还是个人博客&#xff0c;用户对网站的外观和体验要求越来越高。为了确保用户能够轻松访问和使用网站&#xff0c;遵循Web设计规范是至关重要的。本文将探讨一些关键的Web设计规范&…
阅读更多...
Failed to start bean ‘documentationPluginsBootstrapper‘

Failed to start bean ‘documentationPluginsBootstrapper‘

问题描述 在集成redisson-spring-boot-starter时&#xff0c;项目启动时报如下错误 之前在集成swagger3.0的时候&#xff0c;遇到过同样的问题&#xff0c;原因是Springfox使用的路径匹配是基于AntPathMatcher的&#xff0c;而Spring Boot 2.7.X使用的是PathPatternMat…
阅读更多...
使用oracleVM搭建虚拟机

使用oracleVM搭建虚拟机

选择新建&#xff0c;点击 取名字&#xff0c;选择你的安装路径&#xff0c;选择你爹镜像光盘&#xff0c;再勾选下面的&#xff0c;表示跳过一些步骤 其他的都可以默认&#xff0c;下一步即可 创建好了&#xff0c;点击设置&#xff0c;改变光驱&#xff0c;硬盘的顺序 等待它…
阅读更多...
MES管理系统如何实现数据采集和过程控制

MES管理系统如何实现数据采集和过程控制

随着工业4.0的到来&#xff0c;MES管理系统解决方案已成为企业实现生产过程数字化和智能化的关键工具。MES生产管理系统不仅提供生产计划、调度、质量管理和设备维护等功能&#xff0c;还在数据采集和过程控制方面发挥着重要作用。本文将探讨MES生产管理系统如何实现数据采集和…
阅读更多...
智能化追踪与实时管理：RFID技术在流水线上的革命性应用

智能化追踪与实时管理：RFID技术在流水线上的革命性应用

随着科技的不断发展&#xff0c;物联网技术已经深入到了我们生活的方方面面&#xff0c;其中&#xff0c;射频识别&#xff08;Radio Frequency Identification&#xff0c;简称RFID&#xff09;技术被广泛应用于各行各业。在流水线生产中&#xff0c;RFID技术的应用也越来越广…
阅读更多...
跨模态检索：基于OpenAI的Clip预训练模型构建以文搜图系统

跨模态检索：基于OpenAI的Clip预训练模型构建以文搜图系统

目录 1 项目背景 2 关键技术 2.1 Clip模型 2.2 Milvus向量数据库 3 系统代码实现 3.1 运行环境构建 3.2 数据集下载 3.3 预训练模型下载 3.4 代码实现 3.4.1 创建向量表和索引 3.4.2 构建向量编码模型 3.4.3 数据向量化与加载 3.4.4 构建检索web 4 总结 1 项目背景…
阅读更多...
如何数据库备份，如何将数据库备份到其他服务器

如何数据库备份，如何将数据库备份到其他服务器

在当今的数字世界里&#xff0c;数据库已经成为单位和个人存储、管理和检索海量数据的关键工具。然而&#xff0c;随着数据量的增加&#xff0c;内容丢失的风险也随之增加。这就是为什么定期备份数据库变得尤为重要。本文将详细介绍如何有效备份数据库&#xff0c;以保护您的数…
阅读更多...
2023高教社杯数学建模思路 - 复盘：光照强度计算的优化模型

2023高教社杯数学建模思路 - 复盘：光照强度计算的优化模型

文章目录 0 赛题思路1 问题要求2 假设约定3 符号约定4 建立模型5 模型求解6 实现代码 建模资料 0 赛题思路 &#xff08;赛题出来以后第一时间在CSDN分享&#xff09; https://blog.csdn.net/dc_sinor?typeblog 1 问题要求 现在已知一个教室长为15米&#xff0c;宽为12米&…
阅读更多...
五度易链最新“产业大数据服务解决方案”亮相，打造数据引擎，构建智慧产业

五度易链最新“产业大数据服务解决方案”亮相，打造数据引擎，构建智慧产业

快来五度易链官网 点击网址【http://www.wdsk.net/】 看看我们都发布了哪些新功能!!! 自2015年布局产业大数据服务行业以来&#xff0c;“五度易链”作为全国产业大数据服务行业先锋企业&#xff0c;以“让数据引领决策&#xff0c;以智慧驾驭未来”为愿景&#xff0c;肩负“打…
阅读更多...
说点大实话丨知名技术博主 Kirito 测评云原生网关

说点大实话丨知名技术博主 Kirito 测评云原生网关

作者&#xff1a;徐靖峰 关注了阿里云云原生公众号&#xff0c;经常能看到 MSE-Higress 相关的推文&#xff0c;恰逢这次阿里云产品举办了一个 MSE-Higress 云原生网关的测评活动&#xff0c;借此机会体验了一把云原生网关的功能。 购买流程体验 购买网关时&#xff0c;页面明…
阅读更多...
python入门篇04-循环(while与for),变量,函数基础

python入门篇04-循环(while与for),变量,函数基础

python目录 1. 前言1.1 上文传送 2. python基础使用2.1 while循环2.1.1 while循环的使用> 案例: 猜数字游戏(多经典...) 2.1.2 while双层循环> 案例: 输出9*9乘法表> 运行结果 2.2 for循环2.2.1 **for循环使用**> 案例: (字符串)查出有多少字符 2.2.2 方法range()的…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023