文章目录
- 链表
- 1. 链表的基本概念
- 2. 无头非循环单链表实现
- 1) 动态申请节点
- 2) 打印链表元素
- 3) 插入节点
- 头插法
- 尾插法
- 在指定位置之前插入
- 在指定位置之后插入
- 4) 删除节点
- 删除头部节点
- 删除末尾节点
- 删除指定位置之前的节点
- 删除指定位置之后的节点
- 删除指定位置的节点
- 5) 查找元素
- 6) 销毁链表
- 3. 带头循环双向链表实现
- 1) 初始化链表
- 2) 插入节点
- 头插法
- 尾插法
- 指定位置插入
- 3) 打印链表
- 4) 节点删除
- 删除首节点
- 删除末尾节点
- 删除指定位置的节点
- 5) 双向链表的查找
- 6) 销毁链表
- 4. 顺序表对比链表
链表
1. 链表的基本概念
链表是用一组任意的额存储单元存储线性表的数据元素(这组存储单元可以是连续的,也可以是不连续的)。简单来说链表是一种物理结构上非连续,非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。
在数据结构中,链表的结构非常多样,以下情况结合起来有8种结构的链表。
- 单链表,双链表
- 带头,不带头
- 循环,非循环
单链表和双链表结构
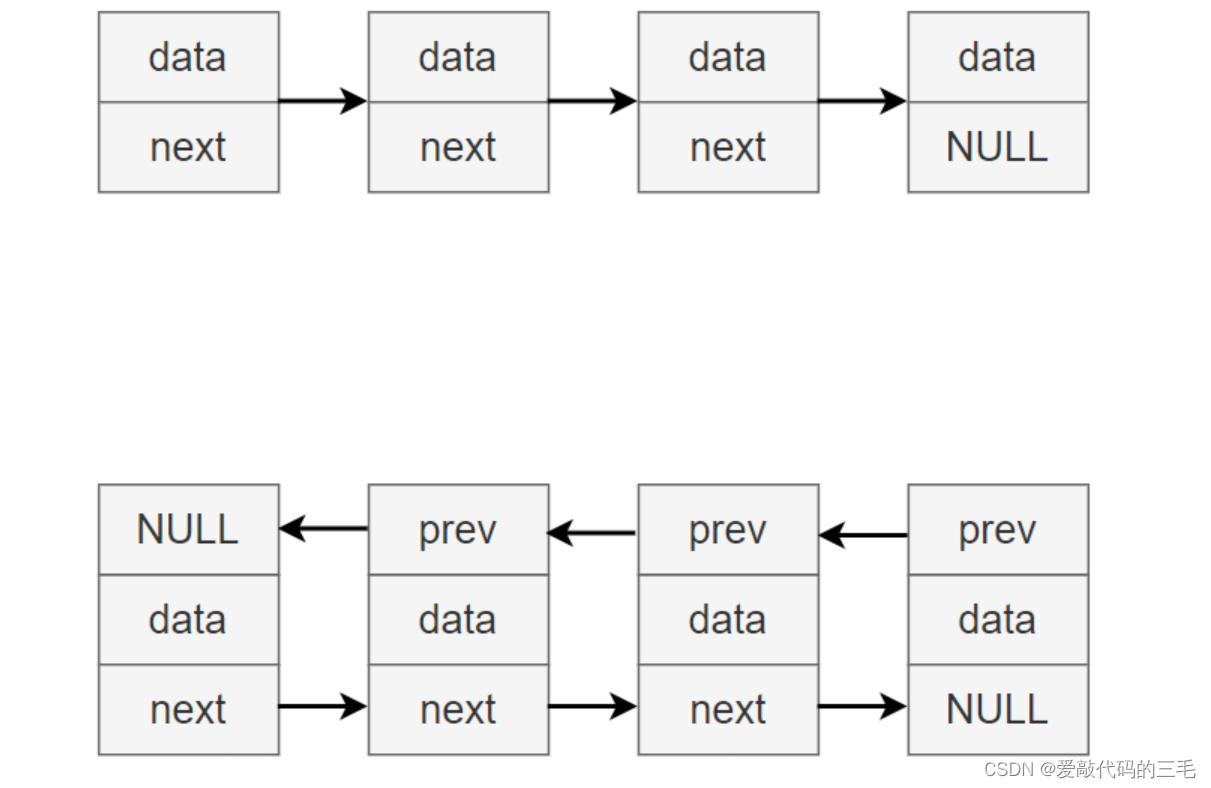
不带头单链表和带头单链表
带头的链表有一个哨兵节点,这个节点不存储数据。它始终是在链表的第一位,头插数据都往它后后面插。
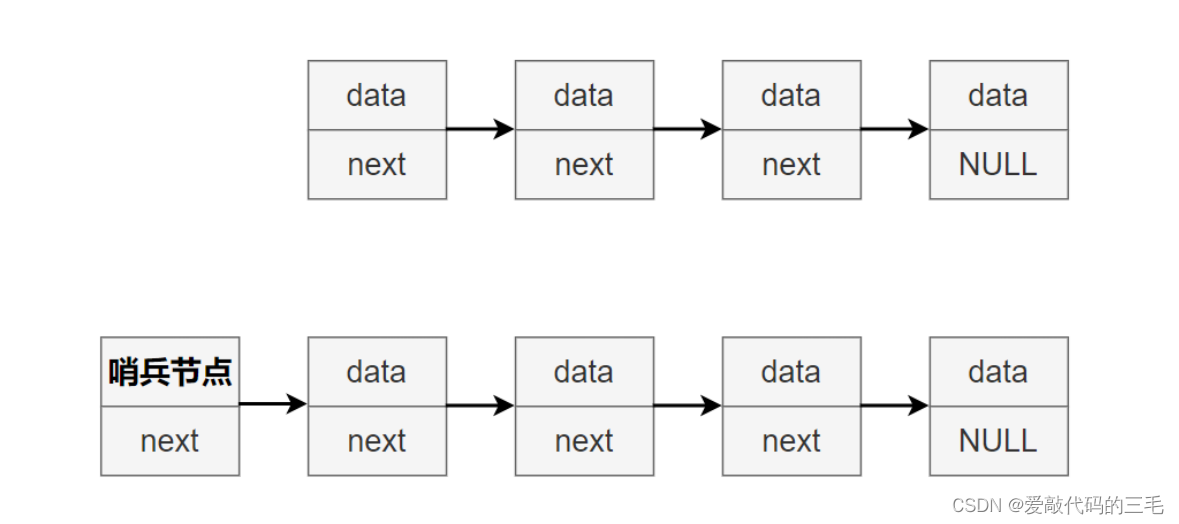
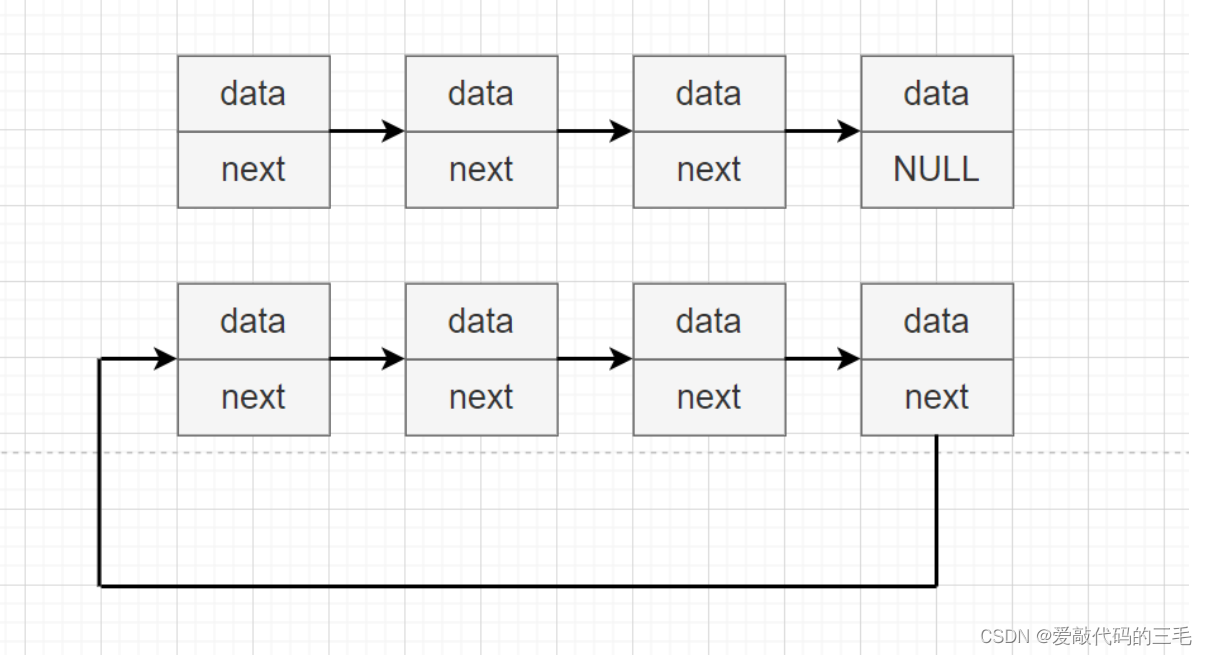
单链表和无头循环单链表
循环单链表它的最后一个元素的指针域存储着头节点的地址
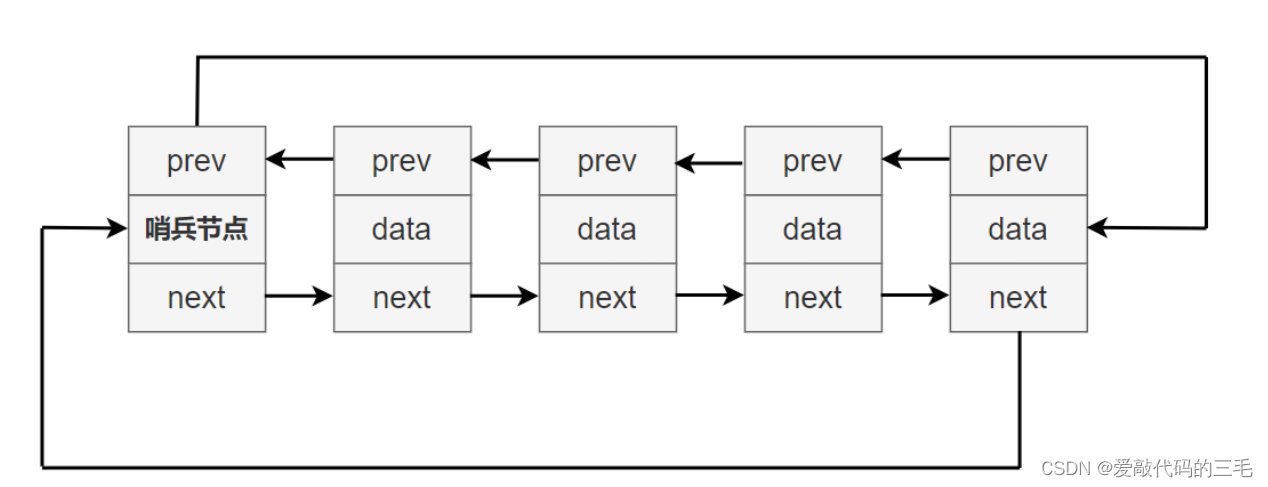
带头循环双链表
双向链表它有3个域,一个存放数据元素,一个存放前一个节点的地址,一个存放后一个节点的地址。这是一个带头且循环的双向链表,它的哨兵节点存prev存放着最后一个节点的低地址,而最后一个节点的next存放的是哨兵节点的地址。
我这里主要实现无头不循环单向链表和带头循环双向链表
2. 无头非循环单链表实现
无头单项非循环链表,结构比较简单,一般不会用来单独存放数据。实际中单链表更多是作为其他高阶数据结构的子结构,比如哈希表、图的邻接表等。
单链表结构
#define SLTDateType int
typedef struct SListNode
{
SLTDateType data;
struct SListNode* next;
}ListNode;
我这里实现一些主要的接口
// 动态申请一个节点
ListNode* BuySListNode(SLTDateType data);
// 尾插法
void SListNodePushBack(ListNode** pList, SLTDateType data);
// 头插法
void SListNodePushFront(ListNode** pList, SLTDateType data);
// 打印链表
void SListNodePrint(ListNode* pList);
// 删除头部元素
void SListNodePopFront(ListNode** ppList);
// 删除末尾元素
void SListNodePopBack(ListNode** ppList);
// 查找元素
ListNode* SListFind(ListNode* pList, SLTDateType data);
// 在pos位置之前插入元素
void SListInsertBefore(ListNode** ppList, ListNode* pos, SLTDateType data);
// 在pos位置之后插入元素
void SListInsertAfter(ListNode** ppList, ListNode* pos, SLTDateType data);
// 删除pos位置的元素
void SListNodePopCurrent(ListNode** ppList, ListNode* pos);
// 删除pos位置之前的元素
void SListNodePopBefore(ListNode** ppList, ListNode* pos);
// 删除pos位置之后的元素
void SListNodePopAfter(ListNode** ppList, ListNode* pos);
// 销毁链表
void SListEraseAfter(ListNode* ppList);
1) 动态申请节点
链表的节点是用一个向堆区申请一个
//动态申请一个节点
ListNode* BuySListNode(SLTDateType data)
{
ListNode* node = (ListNode*)(malloc(sizeof(ListNode)));
if (node == NULL)
{
printf("申请失败\n");
}
else
{
node->data = data;
node->next = NULL;
}
return node;
}
2) 打印链表元素
//打印链表
void SListNodePrint(ListNode* pList)
{
ListNode* cur = pList;
while (cur != NULL)
{
printf("%d->", cur->data);
cur = cur->next;
}
printf("NULL\n");
}
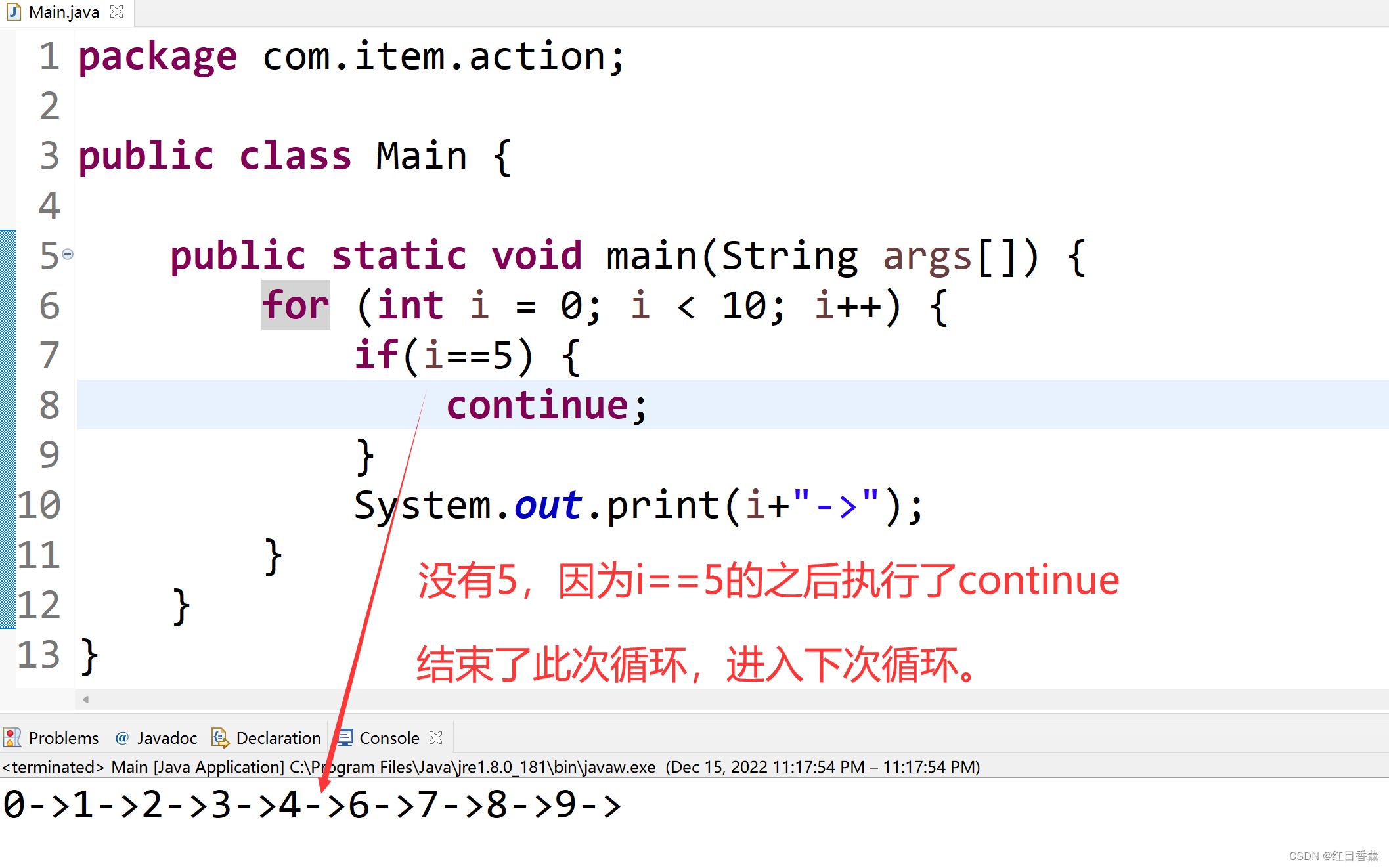
这个代码的时间复杂度为 O ( N ) O(N) O(N)
3) 插入节点
头插法
通过头插法向链表头部插入一个元素,分为以下步
- 判断是否首次插入
- 如果不是首次插入,把申请的节点下一个节点指向头节点,再把头节点指向node节点
//头插法
void SListNodePushFront(ListNode** ppList, SLTDateType data)
{
assert(ppList);
ListNode* node = BuySListNode(data);
//首次插入
if (*ppList == NULL)
{
*ppList = node;
}
else
{
node->next = *ppList;
*ppList = node;
}
}
这个代码的时间复杂度为 O ( 1 ) O(1) O(1)
尾插法
尾插法是向链表末尾插入一个元素
- 同样要判断是否是第一次插入
- 如果不是第一个插入,就遍历到最后一个节点,把最后一个节点的Next指向申请的节点。
//尾插法
void SListNodePushBack(ListNode** ppList, SLTDateType data)
{
assert(ppList);
ListNode* node = BuySListNode(data);
//如果是第一次插入
if (*ppList == NULL)
{
*ppList = node;
}
else
{
ListNode* cur = *ppList;
while (cur->next != NULL)
{
cur = cur->next;
}
cur->next = node;
}
}
这个代码涉及到遍历整个链表,所以时间复杂度为 O ( N ) O(N) O(N)
在指定位置之前插入
在指定位置之前插入元素比较复杂,要考虑两种情况
- 要在头节点之前插入
- 如果是其它位置就需要记录它的前驱节点
//在pos位置之前插入元素
void SListInsertBefore(ListNode** ppList, ListNode* pos, SLTDateType data)
{
assert(ppList && pos);
if (*ppList == pos)
{
//如果要插入的是头节点的位置
//申请节点
ListNode* node = BuySListNode(data);
node->next = *ppList;
*ppList = node;
}
else
{
//遍历到pos位置
ListNode* cur = *ppList;
ListNode* prev = *ppList;
while (cur != NULL)
{
if (cur == pos)//注意这比较的是内存地址
{
//申请节点
ListNode* node = BuySListNode(data);
node->next = pos;
prev->next = node;
break;
}
prev = cur;
cur = cur->next;
}
}
}
这个代码的时间复杂度为 O ( N ) O(N) O(N)
在指定位置之后插入
这个比较简单直接遍历到对应位置就好,注意修改节点指向的代码顺序!
//在pos位置之后插入元素
void SListInsertAfter(ListNode** ppList, ListNode* pos, SLTDateType data)
{
assert(ppList && pos);
ListNode* cur = *ppList;
//遍历到pos位置
while (cur != NULL)
{
if (cur == pos)
{
ListNode* node = BuySListNode(data);
node->next = cur->next;//顺序不能错
cur->next = node;
break;
}
cur = cur->next;
}
}
这个代码的时间复杂度为 O ( N ) O(N) O(N)
4) 删除节点
删除头部节点
拿一个临时遍历记录头节点的位置,再修改后节点的指向,最后free掉要删除的节点。
//删除头部元素
void SListNodePopFront(ListNode** ppList)
{
assert(ppList);
//为NULL情况
if (*ppList == NULL)
{
return;
}
else
{
ListNode* cur = *ppList;
*ppList = (*ppList)->next;
free(cur);
cur = NULL;
}
}
这个代码的时间复杂度为 O ( 1 ) O(1) O(1)
删除末尾节点
删除尾节点需要考虑到三种情况
- 链表为NULL
- 只有一个节点情况
- 多个节点情况
//删除末尾元素
void SListNodePopBack(ListNode** ppList)
{
assert(ppList);
//为NULL情况
if (*ppList == NULL)
{
return;
}
else if ((*ppList)->next == NULL)
{
//只有一个节点情况
free(*ppList);
*ppList = NULL;
}
else
{
//多个节点情况
ListNode* cur = *ppList;
ListNode* prev = *ppList;
while ((cur->next) != NULL)
{
prev = cur;
cur = cur->next;
}
free(cur);
prev->next = NULL;
}
}
这个代码的时间复杂度为 O ( N ) O(N) O(N)
删除指定位置之前的节点
这个操作也要考虑到3种情况
- 如果只有一个节点,或者传递的是头节点是无法删除的
- 有两个节点,要删除的是头节点
- 其他情况
在删除的时候都需要记录要删除的前一个节点的位置!
// 删除pos位置之前的元素
void SListNodePopBefore(ListNode** ppList, ListNode* pos)
{
assert(ppList && pos);
if (*ppList == pos)
{
//要删除的时头节点前面的元素
return;
}
ListNode* cur = *ppList;
ListNode* prev = *ppList;
while (cur != NULL)
{
if (cur->next == pos)
{
if (cur == prev)
{
//要删除的是头节点
*ppList = (*ppList)->next;
free(prev);
prev = NULL;
cur = NULL;
break;
}
else
{
//其他情况
prev->next = cur->next;
free(cur);
cur = NULL;
prev = NULL;
break;
}
}
else
{
prev = cur;
cur = cur->next;
}
}
}
这个代码的时间复杂度为 O ( N ) O(N) O(N)
删除指定位置之后的节点
直接遍历到删除节点之前两个节点进行删除
// 删除pos位置之后的元素
void SListNodePopAfter(ListNode** ppList, ListNode* pos)
{
assert(ppList && pos);
ListNode* cur = *ppList;
while (cur->next != NULL)
{
if (cur == pos)
{
cur->next = cur->next->next;
break;
}
cur = cur->next;
}
}
这个代码的时间复杂度为 O ( N ) O(N) O(N)
删除指定位置的节点
要考虑两种情况
- 要删除的的是头节点
- 其它情况(需要记录删除节点的前驱)
// 删除pos位置的元素
void SListNodePopCurrent(ListNode** ppList, ListNode* pos)
{
assert(ppList && pos);
//如果要删除的是头节点
if (*ppList == pos)
{
*ppList = (*ppList)->next;
}
else
{
ListNode* cur = *ppList;
ListNode* prev = *ppList;
while (cur != NULL)
{
if (cur == pos)
{
prev->next = cur->next;
break;
}
prev = cur;
cur = cur->next;
}
}
}
这个代码的时间复杂度为 O ( N ) O(N) O(N)
5) 查找元素
查找指定节点通过遍历就好,这个代码也可以兼顾修改节点数据。
//查找元素
ListNode* SListFind(ListNode* pList, SLTDateType data)
{
if (pList == NULL)
{
return NULL;
}
ListNode* cur = pList;
while (cur != NULL)
{
if (cur->data == data)
{
return cur;
}
cur = cur->next;
}
return NULL;
}
查找的时间复杂度为 O ( N ) O(N) O(N)
6) 销毁链表
通过双指针直接遍历链表,边遍历边free释放掉节点。
//销毁链表
void SListEraseAfter(ListNode* pList)
{
assert(pList);
ListNode* cur = pList->next;
ListNode* curNext = NULL;
while (cur != NULL)
{
curNext = cur->next;
free(cur);
cur = curNext;
}
free(pList);//释放头节点
}
这个代码的时间复杂为 O ( N ) O(N) O(N)
3. 带头循环双向链表实现
带头双向循环链表结构复杂,一般用于单独存储数据。在实际中使用链表,一般都是带头双向循环链表,虽然这个链表结构复杂,但是实现起来却是比较简单的。带头循环双向链表有以下几个特点:
- 最后一个节点后的下一个节点指向哨兵节点
- 哨兵节点的前一个节点指向链表的最后一个节点
- 头插数据永远往哨兵节点后插
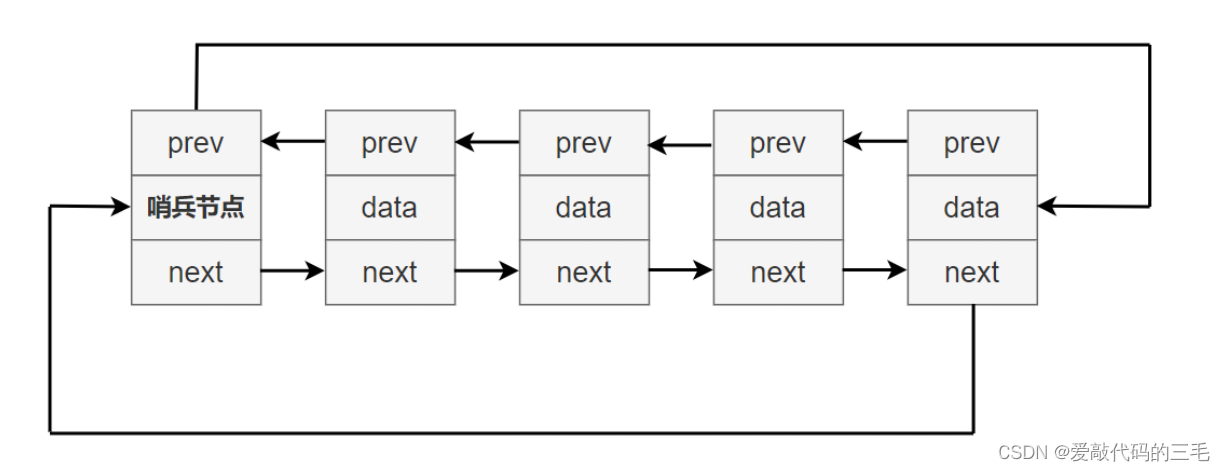
带头循环双向链表结构
typedef int LTDataType;
typedef struct ListNode
{
LTDataType data;//数据
struct ListNode* prev;//节点前驱
struct ListNode* next;//节点后继
}ListNode;
// 动态申请一个节点
ListNode* BuyListNode(LTDataType data);
// 初始化双向链表
ListNode* ListNodeInit();
// 打印双向链表
void ListNodePrint(ListNode* pHead);
// 销毁双向链表
void ListDestory(ListNode* pHead);
// 双向链表头插
void ListNodePushFront(ListNode* pHead, LTDataType data);
// 双向链表尾插
void ListNodePushBack(ListNode* pHead, LTDataType data);
// 双向链表指定位置之前插入
void ListPosInsertBefore(ListNode* pHead, ListNode* pos, LTDataType data);
// 双向链表指定位置之后插入
void ListPosInsertAfter(ListNode* pHead, ListNode* pos, LTDataType data);
// 双向链表删除首节点
void ListNodePopFront(ListNode* pHead);
// 双向链表删除尾节点
void ListNodePopBack(ListNode* pHead);
// 双向链表删除指定位置节点
void ListNodePopCurrent(ListNode* pHead, ListNode* pos);
// 双向链表的查找
ListNode* ListNodeFind(ListNode* pHead, LTDataType data);
1) 初始化链表
要想初始化链表必须要有申请节点,所以封装一个函数来申请节点。
// 动态申请一个节点
ListNode* BuyListNode(LTDataType data)
{
ListNode* newNode = (ListNode*)(malloc(sizeof(ListNode)));
if (newNode == NULL)
{
printf("空间申请失败\n!");
exit(-1);
}
newNode->data = data;
newNode->prev = NULL;
newNode->next = NULL;
return newNode;
}
带头循环的双向链表初始化要先申请一个节点作为哨兵节点,这个节点不存放数据起一个标识作用,它永远位于首节点前面。初始化时先让哨兵节点的前驱和后继都指向自己。
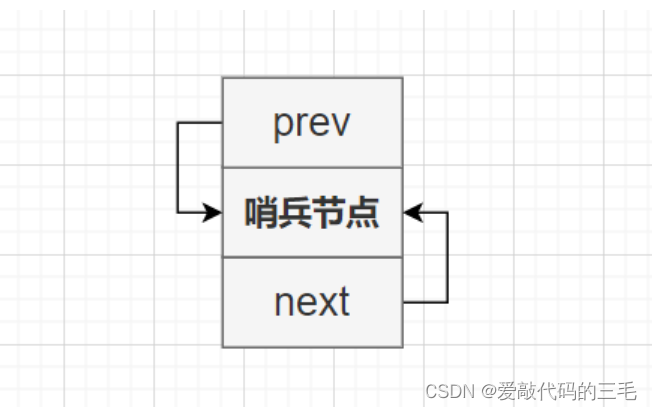
// 初始化双向链表
ListNode* ListNodeInit(LTDataType data)
{
// 申请一个头节点作为哨兵节点
ListNode* head = BuyListNode(data);
//让这个哨兵节点的前驱和后继都先指向自己
head->prev = head;
head->next = head;
return head;
}
2) 插入节点
头插法
头插法只需要把新节点插入到哨兵节点后面就可以了,注意修改 节点指向顺序
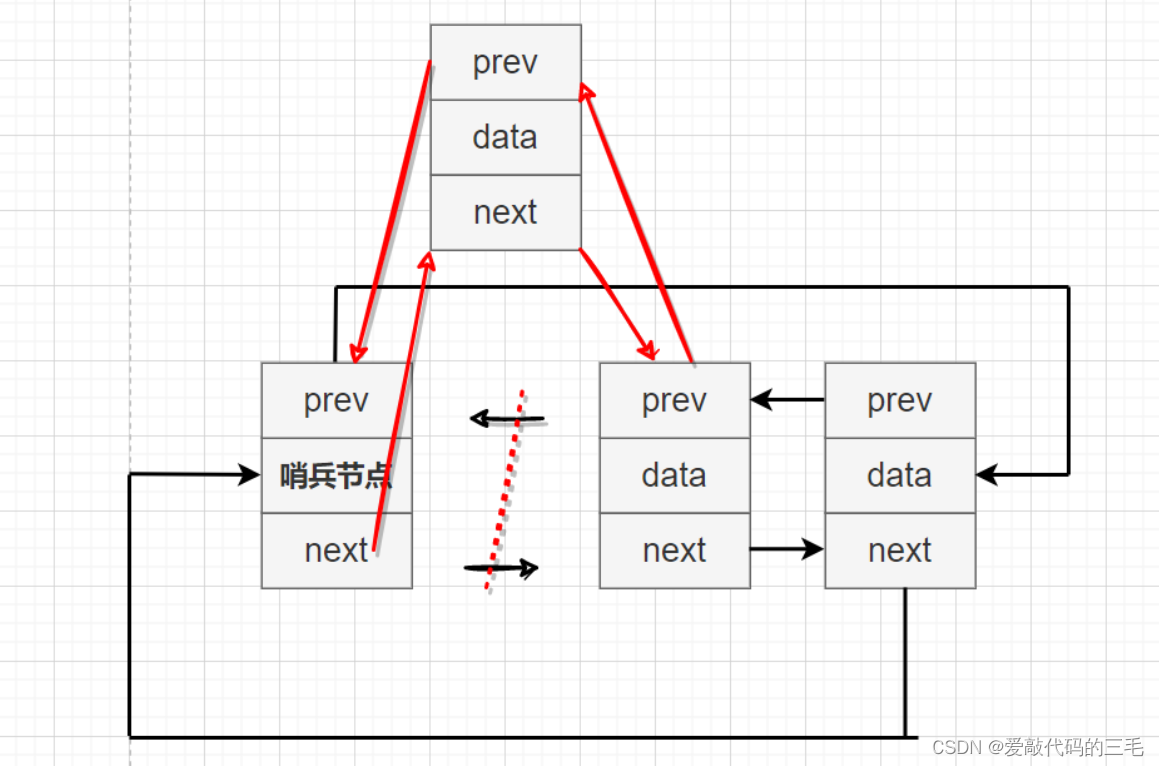
// 双向链表头插
void ListNodePushFront(ListNode* pHead, LTDataType data)
{
assert(pHead);
ListNode* node = BuyListNode(data);
//头插一律插到哨兵头节点后面
node->next = pHead->next;
node->prev = pHead;
pHead->next->prev = node;
pHead->next = node;
}
尾插法
尾插法和头插法类似,只不过它是把节点插到链表的末尾。
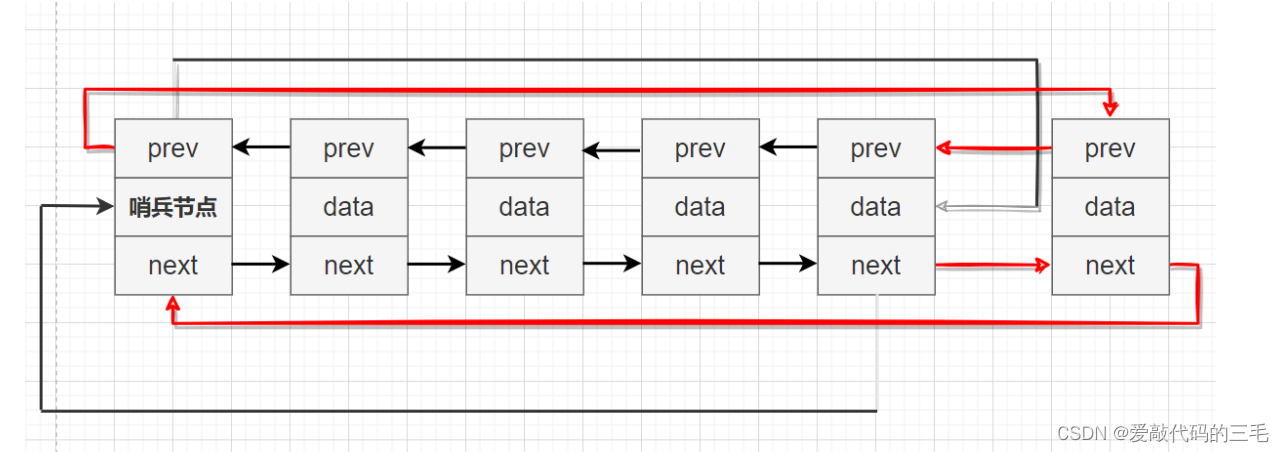
// 双向链表尾插
void ListNodePushBack(ListNode* pHead, LTDataType data)
{
assert(pHead);
ListNode* node = BuyListNode(data);
node->next = pHead;
node->prev = pHead->prev;
pHead->prev->next = node;
pHead->prev = node;
}
指定位置插入
指定位置前或者指定位置后插入,比较简单只需要修改指向即可。
指定位置之前插入
// 双向链表指定位置之前插入
void ListPosInsertBefore(ListNode* pHead, ListNode* pos, LTDataType data)
{
assert(pHead && pos);
ListNode* node = BuyListNode(data);
node->prev = pos->prev;
pos->prev->next = node;
pos->prev = node;
node->next = pos;
}
指定位置之后插入
// 双向链表指定位置之后插入
void ListPosInsertAfter(ListNode* pHead, ListNode* pos, LTDataType data)
{
assert(pHead && pos);
ListNode* node = BuyListNode(data);
node->next = pos->next;
pos->next->prev = node;
pos->next = node;
node->prev = pos;
}
3) 打印链表
因为这是带头循环链表,所以要从哨兵节点后一个节点开始遍历,知道遇到哨兵节点就结束遍历
// 打印双向链表
void ListNodePrint(ListNode* pHead)
{
assert(pHead);
ListNode* cur = pHead->next;
while (cur != pHead)
{
printf("%d->", cur->data);
cur = cur->next;
}
printf("NULL\n");
}
4) 节点删除
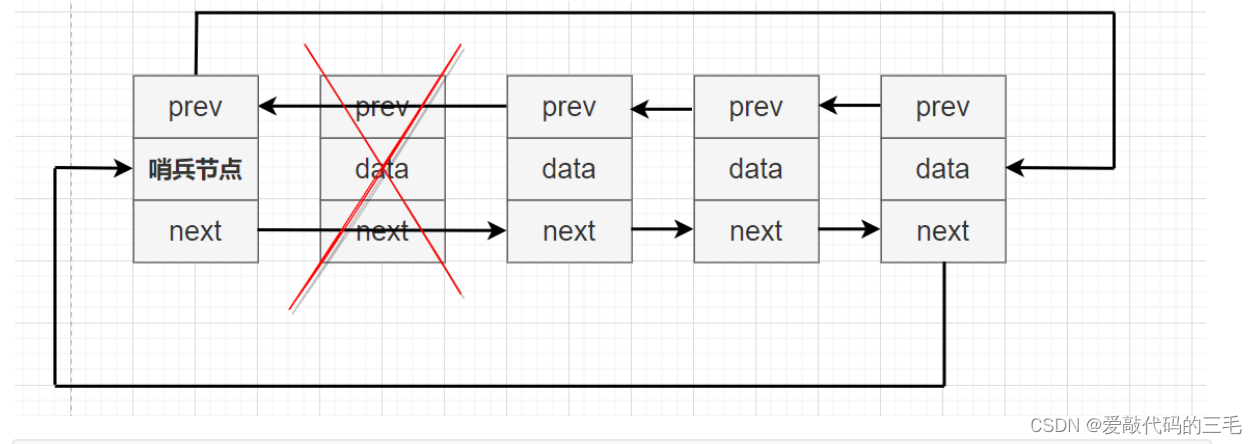
删除首节点
注意删除的不是哨兵节点,而是首节点,也就是哨兵节点后面那一个节点
// 双向链表删除首节点
void ListNodePopFront(ListNode* pHead)
{
assert(pHead);
if (pHead->next == pHead)
{
//没有节点
return;
}
ListNode* cur = pHead->next;
pHead->next = cur->next;
cur->next->prev = pHead;
free(cur);
}
删除末尾节点
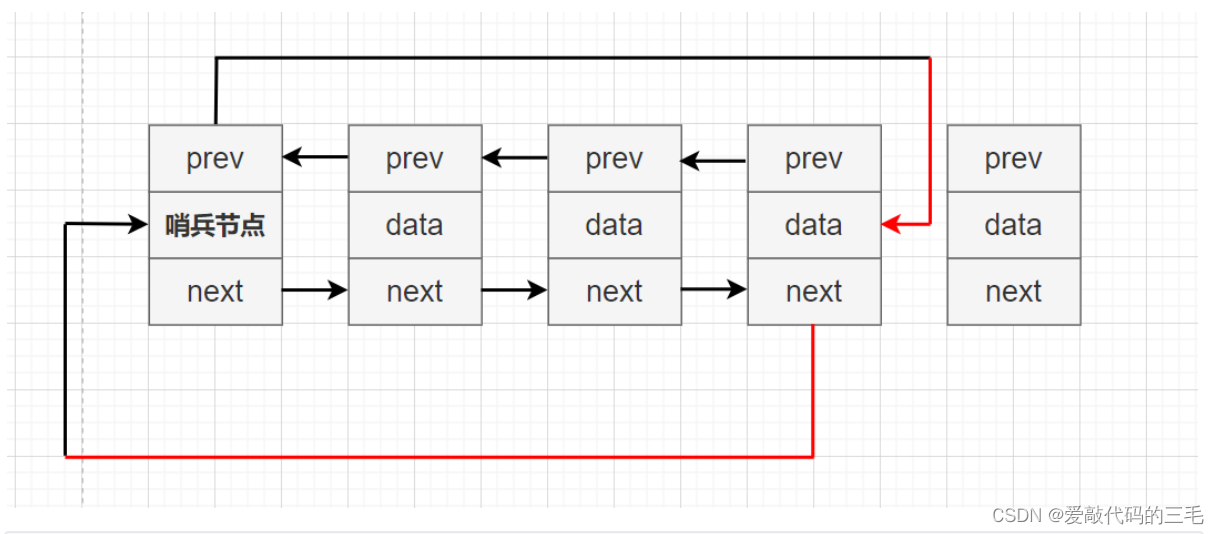
// 双向链表删除尾节点
void ListNodePopBack(ListNode* pHead)
{
assert(pHead);
if (pHead->prev == pHead)
{
//没有节点
return;
}
ListNode* cur = pHead->prev;
pHead->prev = cur->prev;
cur->prev->next = pHead;
free(cur);
}
删除指定位置的节点
这个只要注意修改指向顺序即可
// 双向链表删除指定位置节点
void ListNodePopCurrent(ListNode* pHead, ListNode* pos)
{
assert(pHead && pos);
pos->prev->next = pos->next;
pos->next->prev = pos->prev;
free(pos);
}
5) 双向链表的查找
和打印类似都是遍历
// 双向链表的查找
ListNode* ListNodeFind(ListNode* pHead, LTDataType data)
{
assert(pHead);
ListNode* cur = pHead->next;
while (cur != pHead)
{
if (cur->data == data)
{
return cur;
}
cur = cur->next;
}
return NULL;
}
6) 销毁链表
// 销毁双向链表
void ListDestory(ListNode* pHead)
{
assert(pHead);
ListNode* cur = pHead->next;
ListNode* curNext = NULL;
while (cur != pHead)
{
curNext = cur->next;
free(cur);
cur = curNext;
}
//最后删除哨兵节点
free(pHead);
}
4. 顺序表对比链表
顺序表的优点:
- 顺序表支持随机访问
- 顺序表的cpu高速缓存命中率高(物理空间是连续的)
顺序表的缺点:
- 空间不够需要扩容扩容存在着一定的内存消耗,可能存在着一定的空间浪费
- 在头部或者中间插入删除元素需要挪动元素,时间复杂度为 O ( N ) O(N) O(N),效率较低。
链表的优点:
- 按需申请,不存在空间浪费
- 任意位置插入的时间复杂为 O ( 1 ) O(1) O(1)(不包括遍历)
链表的缺点:
- 不支持下标的随机访问
如何理解,顺序表的cpu高速缓存命中率高,链表的高速缓存命中率低
我们知道CPU的访问速度是远远高于内存的,高速缓存就是为了平衡CPU和内存中间的性能差异,分为 L1、L2、L3 三种高速缓存。
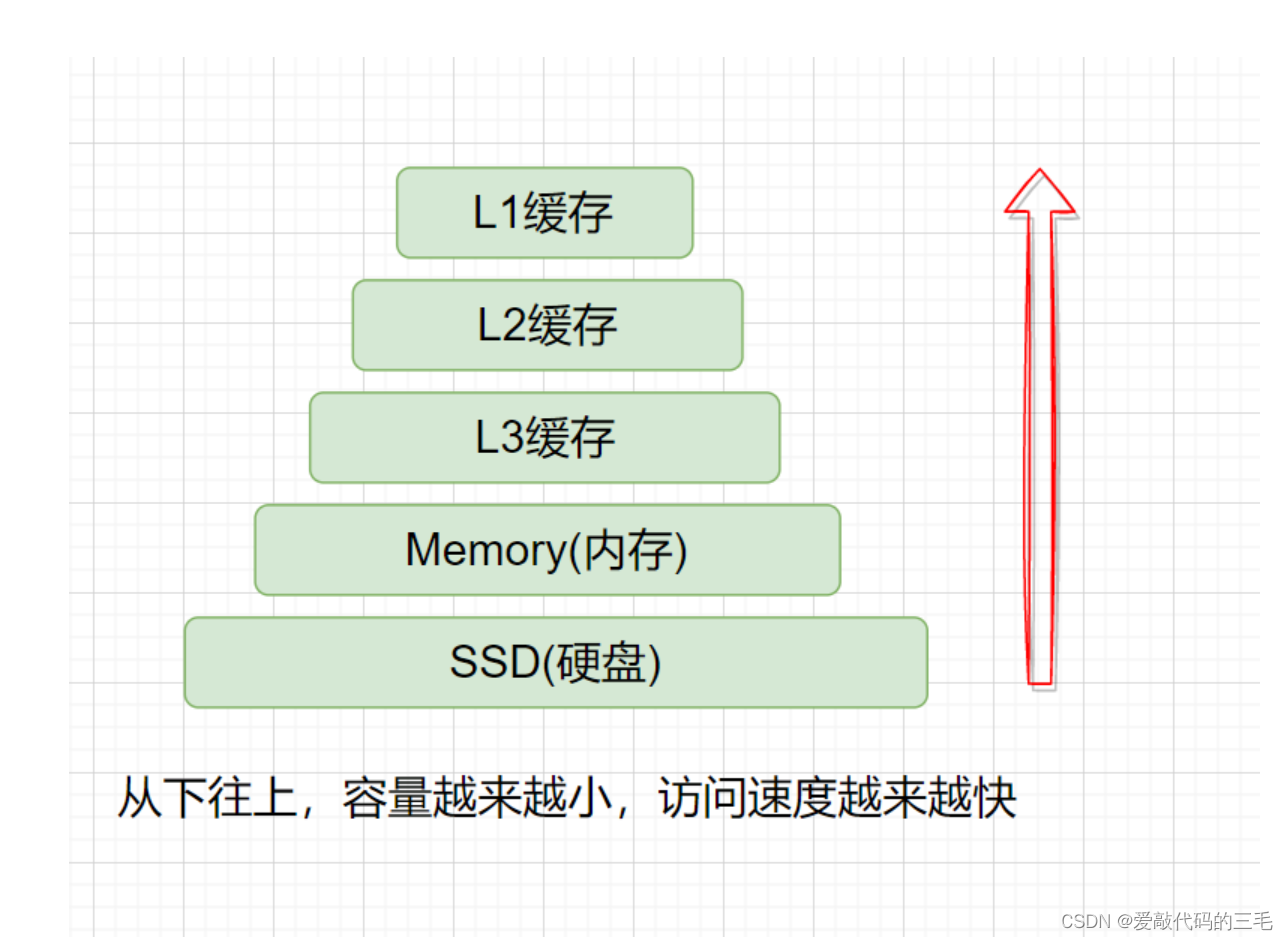
CPU在访问内存的时候会进行预加载,把一部分数据加载到高速缓存中。CPU就会先看高速缓存中是否存在需要的数据,如果存在就是命中,不存在就是没有命中,没有命中的数据。
假设我们要打印顺序表和链表。
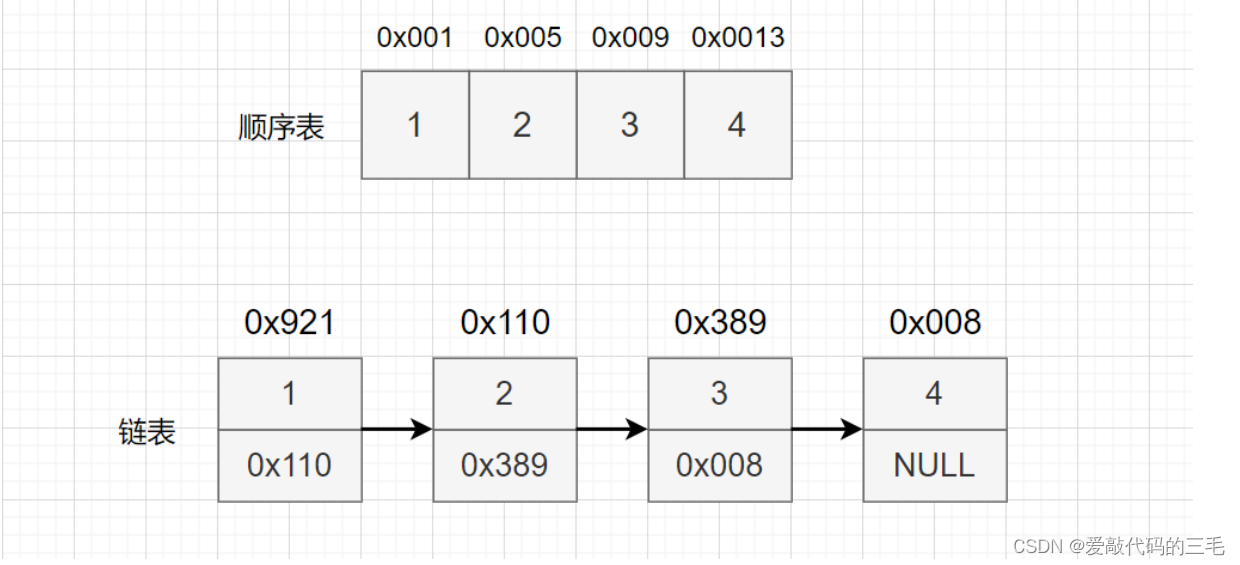
我们知道顺序表的物理空间是连续的,假设高速缓存行中一次性加载64个字节。内存到高速缓存中去看发现没有我们需要的数据(未命中),就会进行预加载(通过地址找到对于的数据)。一次性把0x001后面连续64个字节的数据加载进来,之后每次打印的数据都在高速缓缓存中存在,所以都是命中的。
而如果打印的是链表,那么内存去高速缓存中看没有数据,就会把头节点的0x921后连续的64个字节加载到高速缓存中,接着打印0x110,因为链表在物理上不是连续的,所以在高速缓存中不存在数据,就又会进行预加载,就这样不断预加载打印、预加载打印,都是没有命中的。低命中会照成缓存污染,效率也会更低。









![leetcode 337. 打家劫舍 III-[python3图解]-递归+记忆化搜索](https://img-blog.csdnimg.cn/c2421d8064474305a66dd207bd8296c9.png)