DDD领域驱动设计批评文集
“软件方法建模师”不再考查基础题
《软件方法》各章合集
我写了一篇文章,批评付施威的《DDD诊所——聚合过大综合症》(以下简称《DDD诊所》),文章是《你的医书是假的!批评付施威的《DDD诊所——聚合过大综合症》》(以下简称《你的医书是假的》)。
一、《你的医书是假的》关键内容
《DDD》诊所说,下面这个是不变式:
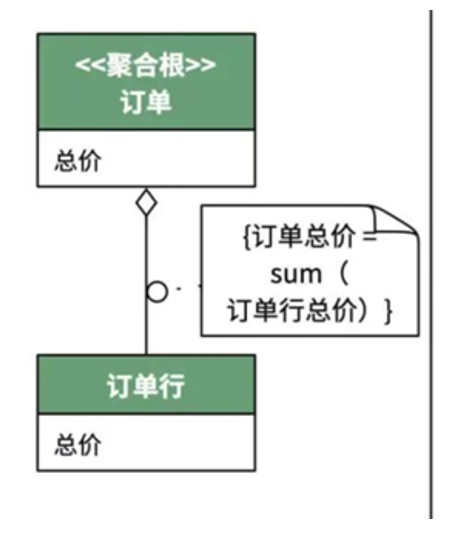
图1 《DDD诊所》截图
我在《你的医书是假的》中提出以下批评:
(1)不变式是类的不变式。《DDD诊所》作者把它放在关系上是不对的,说明该作者没有理解不变式。
(2)《DDD诊所》作者引用的《领域驱动设计》译文的翻译很糟糕(参见《猴子掰玉米?比较不同版《领域驱动设计》说“不变式”和“聚合”》),关键内容的意思译反了,而《DDD诊所》作者并无察觉,反而整段引用作为依据。
(3)不变式不是用来描述像图中的“订单总价=sum(订单行总价)”这样的内容的。如果这样的约束被严格遵守,说明“订单”的“总价”属性在逻辑上是冗余的,应该删掉。既然“总价”属性没了,图1的所谓“不变式”自然也就没有了。
也就是说,改变订单属性值(包括加/删订单行以及其他操作)的时候,不需要判断某个含有“总价”属性的表达式是否为真——实际上也没法判断,“总价”属性都没有了嘛。
接下来,我再针对图1做进一步的阐述,帮助进一步理解不变式,并评点在《你的医书是假的》文章下面的留言。
二、等号和赋值号没搞混吧?
不变式是一个布尔表达式。
我在这里提这一点,到底是什么意思呢?
意思是:
如果发现有“不变式”表示为相等关系的表达式,那就要警惕一下,建模人员是不是把“=”当成赋值来理解了。
例如,图1的式子“订单总价=sum(订单行总价)”,有可能就会被误解成“把订单项的价钱之和赋值给订单总价以同步这两边的值”。
读者可以注意到,我在《你的医书是假的》画的图例中,没有相等关系的不变式。
读者还可以对比下面的例子:

图2 三角形及其不变式
这个还行,对吧?
那读者再看这个:

图3 错例:等边三角形及其不变式?
这个是不是比较诡异?不过,这样的图倒是符合DDD伪创新的口味:投资少、见效快、门槛低、产量高、仪式感十足。
注意,我在图3中用“==”表示相等关系,而不是用“=”。其实这是违反OCL语法的,OCL里就是“=”表示相等关系,和SQL类似,但考虑到上面说的赋值误解(特别是显示在类图上时),我倒是觉得OCL应该改一下。
那么,可不可以有相等关系的不变式?可以有,但很少。相等关系表达式,经常是出现在前置条件和后置条件,而不是不变式。
什么时候可以有相等关系的不变式,这个就涉及到相当多的知识,不是本文能装得下的了,感兴趣的读者可以关注我的《软件方法》。
三、“订单总价=sum(订单行总价)”的另一个问题
这个问题在《你的医书是假的》中没指出来,在这里补上:
“订单总价=sum(订单行总价)”这个所谓的“不变式”,和图1中的属性名、关联角色名对不上。
图1中的属性名、关联角色名没有“订单总价”和“订单行总价”,只有“订单.总价”、“订单行.总价”——这也说明《DDD诊所》作者当时没有理解不变式是干什么用的。
四、不变式在哪里实现?
上面说了,不变式是一个布尔表达式,它只是说,对象的属性值不能违反这个约束,至于如何保证这一点,它没有做任何指定或暗示。
例如,把每一个不变式封装成一个方法,如果某个操作会修改某不变式中所涉及到属性的值,就调用相应方法来检查——这个工作可不轻松。
如果所用的实现技术支持前置条件、后置条件、不变式等契约编程,例如.NET中提供的Contract类,使用该类提供的服务即可。
五、类似“sum(订单行总价)”的运算会出现在哪里?
可能会有人问这样的问题。
类似“sum(订单行总价)”的运算,像其他针对各个属性的各种运算一样,并没有什么特别,会出现在类的某个操作或多个操作里。
什么操作?正确的回答是“信息不足,不知道”,可能“订单”专门有一个“计算总价”的操作,“sum(订单行总价)”藏在该操作的实现中,也可能“订单”根本不需要有“计算总价”的操作,“sum(订单行总价)”藏在“订单”的某个更复杂的操作的实现中。
不管怎么样,这和图1那个相等关系的“不变式”不存在什么有规律的对应关系。
六、关于付施威的解释
《DDD诊所》作者付施威在《你的医书是假的》的评论区留言解释:

图4 《DDD诊所》作者付施威的解释
先说解释中的第3点:
如果还有“订单总价<3000”这样的约束,之前的结论也没有变化,只不过“订单”的不变式多了一个:
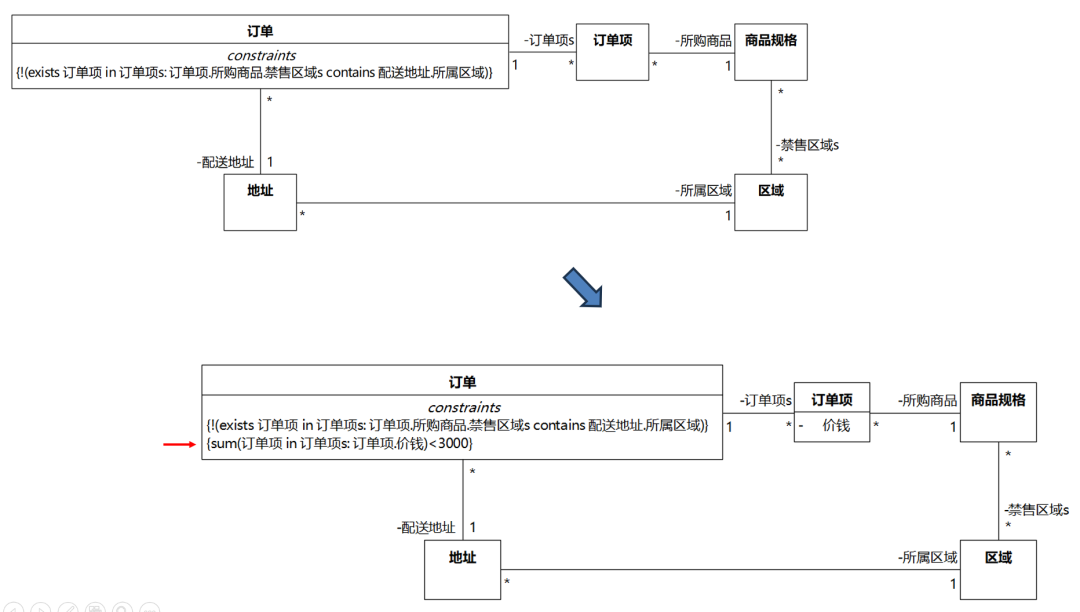
图5 加上订单总价<3000后的类图变化(注:我把类名和属性名改成订单项.价钱)
再说解释中的第1点:
付施威谦虚地解释“DDD诊所是内部活动”、“主要职责是被人研究”,但下面的海报传递出来的信息似乎是不一样的。

图6 活动海报1

图7 活动海报2
开直播以专家身份传道授业解惑没问题,但被指出问题了,又谦虚地说是学习体会,这个似乎就不太好。
*********
未完待续……
▲关于林宁的评论