文章目录
- 前言
- 大数相加
- 大数相减
- 大数乘法
- 除法
- 总结
前言
OK,继续预热哈,没办法还得补作业,要G了,明天看看有没有时间加更一篇。
那么今天的话还是来说一下这个精度的一些问题,也就是大数之类的一些问题啥的。这个当然咱们以前也是也过的,今天主要就是做系列嘛。
大数相加
首先这个的话,如果咱们是这个python的话显然就是没有必要再讲下去的,包括java的也没有必要。但是的话,这个基本的一些东西还是要说的,毕竟底层还是这样实现的嘛。毕竟使用python完成1+1=2虚拟机做了相当多的工作的。
这里的话我们来一下整数的大数相加,首先我们都知道,一个数字是按照一个比特进行存储的,也就是按照一个一个位数进行存储的,那么我们要实现这个大数相加的话,其实就是需要去模仿一下正常的手算的一个过程。
这个说实话用python写还是怪怪的,有点那啥的意思。
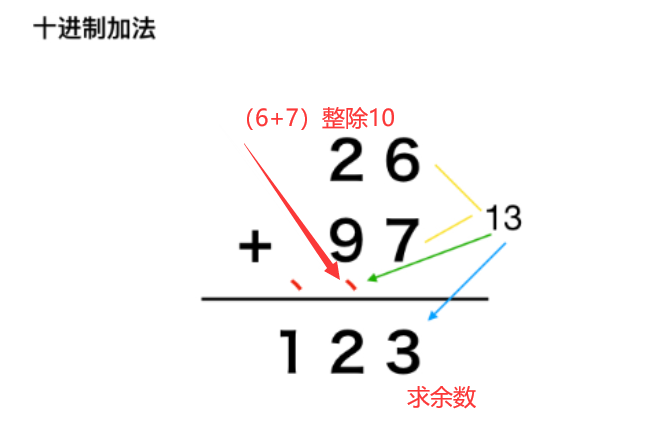
核心就是相加进位呗,我们通过求余数操作得到当前位数的数字,通过整数操作得到进位的大小。其实就这样:
OK,那么代码的话就非常简单:
那么在这个代码里面我们需要注意的是什么呢,其实很简单,我们低位数是放在最前面的,为什么这样做呢,很简单,我们要进位,如果我们是按照上面的图例进行相加的话,那么当需要进位的时候,例如99+1
def bigadd(a:str,b:str):
target_a = [int(a[i]) for i in range(len(a)-1,-1,-1)]
target_b = [int(b[i]) for i in range(len(b)-1,-1,-1)]
c = 0
res = ""
stop = len(a) if len(a)<len(b) else len(b)
for i in range(stop):
res+=str(((target_a[i]+target_b[i])%10)+c)
c = (target_a[i]+target_b[i])//10
end = target_a if len(a) > len(b) else target_b
for i in range(stop,len(end)):
res+=str((end[i]+c)%10)
c = (end[i]+c)//10
if(c!=0):
res+=str(c)
result = ""
for i in range(len(res)-1,-1,-1):
result+=res[i]
return result
在模拟的时候,我们需要注意的其实就是相加的时候,这个数组的长度,如果是相同的怎么处理,如果是不相同的时候怎么处理,最后记得把最后一个进位加上。
也就是这几部分:

当然这个还是模拟我们手动去做,那么实际上的话我们是有模板的,而且模板实现起来非常简单:
首先,我们先保证就是说,我们的输入的两个数字已经转化为了数组,并且是逆序的,也就是说从高位到低位排序的,那么我们就这样干,这里的话我给一个C的模板,写起来简洁一点儿。
vector<int> add(vector<int> &A,verctor<int>&B)
{
vector<int> C;
int t=0;
for(int i=0;i<A.size()||i<B.size();i++)
{
if(i<A.size()) t+=A[i]
if(i<B.size()) t+=B[i]
C.push_back(t%10);
t/=10;
}
if(t) C.push_back(1);
return C;
}
然后的重新逆序遍历之后就是答案。
大数相减
有了加法我们必然是有减法的,这个的话我们同样的如果模拟我们手动操作的话就是这样的:
def bigsub(a:str,b:str):
target_a = [int(a[i]) for i in range(len(a)-1,-1,-1)]
target_b = [int(b[i]) for i in range(len(b)-1,-1,-1)]
res = ""
c=0
if(len(target_a)<len(target_b)):
target_a,target_b = target_b,target_a
stop = len(a) if len(a) < len(b) else len(b)
for i in range(stop):
temp = (target_a[i]+10-target_b[i])+c
res+=str(temp%10)
c = 0 if(temp>=10) else -1
end = target_a if len(a) > len(b) else target_b
for i in range(stop,len(end)):
temp = end[i]+c+10
res+=str(temp%10)
c = 0 if (temp >= 10) else -1
result = ""
for i in range(len(res)-1,-1,-1):
result+=res[i]
result = result.lstrip('0')
if (len(target_a) > len(target_b)):
result = "-"+result
return result
同样的我们需要做一个逆序,我们在从个位开始相减。
那么我们这里的区别其实就是那个c,也就是进位的一些区别。如果相减去小于0那么就需要进行一个借位,当然这里的话我先加了一个10,效果是一样的,只是我不太喜欢0而已。
同样的,咱们还是有模板的,这个咱们也直接使用C++ 进行一个模板的编写,python写起来不是那么美观,当然用python的话也用不上这个。
vector<int> sub(vector<int> &A,vector<int> &B)
{
vector<int> C;
for(int i=0,t=0;i<A.size();i++)
{
t = A[i] -t;
if(i<B.size()) t-=B[i];
C.push_back((t+10))%10);
if(t<0) t=1;
else t=0;
}
while(C.size()>1 && C.back()==0)c.pop_back();
return C;
}
当然这个模板的局限性是有的,刚刚的python代码多了一点东西,但是其实都是一样的。
大数乘法
那么此时的到了咱们的整个乘法的时刻了,对于乘法可以是很大的数字乘以一个不是很大的数字,也可以是两个很大的数字相乘。
那么这个的话,我们还是先来说一下比较简单的情况,因为这块乘法的话咱们也是有进位的对吧。
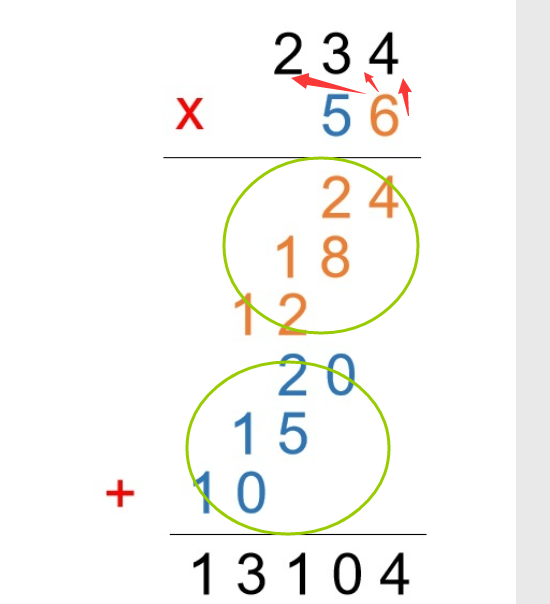
首先是在下面的那个数字,的个位开始相乘对吧,之后的话我们会得到两个行的数据,也就是我们圆圈圈起来的地方。
之后我们做加法就好了。
所以的话,如果我们做这样的乘法的话,我们其实还是和加法整合在了一起。这里的话我们还是来看到我们具体的代码来:
def mul_add(target_a:list,target_b:list):
c = 0
res = []
stop = len(target_a) if len(target_a) < len(target_b) else len(target_b)
for i in range(stop):
res.append(((target_a[i] + target_b[i]) % 10) + c)
c = (target_a[i] + target_b[i]) // 10
end = target_a if len(target_a) > len(target_b) else target_b
for i in range(stop, len(end)):
res.append((end[i] + c) % 10)
c = (end[i] + c) // 10
if (c != 0):
res.append(c)
return res
def bigmul(a:str,b:str):
target_a = [int(a[i]) for i in range(len(a)-1,-1,-1)]
target_b = [int(b[i]) for i in range(len(b)-1,-1,-1)]
res = ""
if(len(target_a)!=len(target_b)):
down = target_a if len(a)<len(b) else target_b
up = target_b if len(a)<len(b) else target_a
else:
down = target_a
up = target_b
rows = []
for muls in range(len(down)):
c = 0
#这里我得到的结果是反过来的,所以需要在开始的时候注意补位
row=[0 for _ in range(muls)]
for i in range(len(up)):
row.append(c+((down[muls]*up[i])%10))
c = (down[muls]*up[i])//10
if(c!=0):
row.append(c)
rows.append(row)
#此时我们的加法就是变成了好几个数字一起相加了,那么这个时候
#我们仿造加法当中的两两相加就好了。
if(len(rows)==2):
res = mul_add(rows[0], rows[1])
elif(len(rows)>=2):
for j in range(2,len(rows)-1):
res = mul_add(res,rows[j])
else:
res = rows[0]
result = ""
for i in range(len(res)-1,-1,-1):
result+=str(res[i])
return result
首先一开始的话,我们还是需要做逆序处理。如果是C++,那么直接使用Vector,那么我们这边是python,就直接使用list来实现。那么首先的话,我们可以看到这个代码:
rows = []
for muls in range(len(down)):
c = 0
#这里我得到的结果是反过来的,所以需要在开始的时候注意补位
row=[0 for _ in range(muls)]
for i in range(len(up)):
row.append(c+((down[muls]*up[i])%10))
c = (down[muls]*up[i])//10
if(c!=0):
row.append(c)
rows.append(row)
至于前面的话,其实就是在判断是在上面,谁在下面,就是谁更大嘛。我们模拟手算的话,我们打的要在上面。那么第一个循环我们是拿到下面的数字的个位数先进行一个乘法,之后的话进行一个进位,按照上面的图片的例子,我们其实就是得到刚刚圈起来的两个地方求和得到数字,按照例子就是:1404和1170,之后的话我们把这两个家伙相加就好了。
#此时我们的加法就是变成了好几个数字一起相加了,那么这个时候
#我们仿造加法当中的两两相加就好了。
if(len(rows)==2):
res = mul_add(rows[0], rows[1])
elif(len(rows)>=2):
for j in range(2,len(rows)-1):
res = mul_add(res,rows[j])
else:
res = rows[0]
result = ""
for i in range(len(res)-1,-1,-1):
result+=str(res[i])
return result
当然我们这边做都是逆序来的。为什么前面已经说了。但是这里还有个点需要注意的就是,我们的进位问题,我们首先是逆序的,然后的话,我们是错位相加的,所以一开始咱们的这个代码部分是有加0的操作
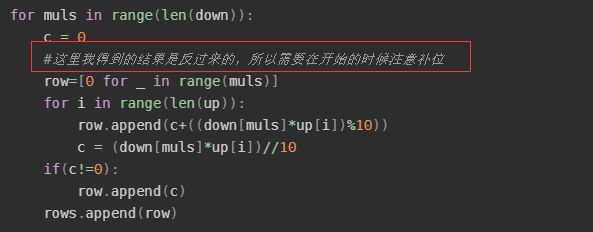
当然,咱们还是来一点简单的,那么我们来一个模板,就是大数乘以一个相对较小的数的模板:
这个模板也是用C++ 来写,因为更简洁一点点儿。
vector<int> mul(vector<int> &A, int b)
{
vector<int> C;
int t = 0;//进位
for(int i=0;i<A.size() || t;i++)
{
if(i<A.size()) t+=A[i]*b;
C.push_back(t%10);
t/=10;
}
return C;
}
刚刚那个python版本的话是大数乘以大数的时候这样干。
除法
之后的话是我们的除法,这个稍微复杂一点点。这个和我们一般的习惯上有一点点的区别,就是咱们这边计算机求取这个商的话,计算机是来一位一位去求,因为不是人嘛。它看不出来那个商是啥。
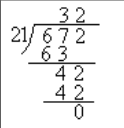
这是我们人来求取这个玩意,那么如果是计算机的话一开始是这样的:

首先r是余数,一开始余数是0
之后的话,6-0还是6
此时进入下一位计算是6*10+7=67
之后我们再算二者相减的差然后乘以10+2=42
此时我们可以发现就是:商 = 余数//被除数
此外相差为r%被除数的余数。(其实如果你看过python3的对于余数的计算的话,你其实会发现图中得到4这个结果其实就是官方对于python除数运算结果的解释)
OK,现在我们来开始编写一个模板:
首先的话,我们还是逆序存储,因为这个确实不是那么好写,大数/大数的,所以的话,我们这边个懒吧,因为这里的话涉及到更多的一些东西去优化,这个要到后面来说。所以先埋个坑,我们后面再来考古。
vector<int> div(vector<int> &A,int b,int &r)
{
vector<int> C;
r = 0;
for(int i=A.size()-1;i>=0;i--)
{
r = r*10+A[i];
c.push_back(r/b);
r%=b;
}
//此时商是正序的,如果需要逆序输出的话,那么我们还需要逆序一下
resverse(C.begin(),C.end());
while(C.siez()>i && C.back()==0) C.pop_back();
return C;
}
总结
OK,今天的话就先这样吧,强行返乡,还没结课呢