一 准备
1 给定数据集 D={(
),(
),...,(
)},其中假设X是一维的情况，即只有一个自变量
2 线性回归学习的目标：
,使得
3 如何确定w和b？关键在于衡量f(x)和y之间距离的方法，此处使用的是‘均方误差’，其具有非常好的几何意义，对应了常用的欧几里得距离；公式如下：
因此我们可以试图让均方误差最小化，即：
4 ‘最小二乘法’：基于“均方误差”来进行模型求解的方法；其试图找到一条直线，使所有样本到直线的欧氏距离之和最小。
5 “线性回归模型的最小二乘参数估计”：求解w和b使
最小化的过程
6 为简化公式，以下
均用
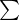代替
二 估计过程
1.最小化目标函数：
（1）
2.我们将
分别对w和b求导；
1）首先化简等式
2)对
求w的偏导
3)对
求b的偏导 先进一步化简等式：
再求偏导：
4)整理上述两个偏导求取结果
3.另2中求得的两个偏导数结果为0可得w和b的最优闭式解
1）首先令
等于0
2) 再令
等于0
(代入b的表达式)
（其中,
,为x的均值）
三 参考文献
机器学习 周志华 清华大学出版社 2016年1月第一版
