姜启源数学模型第五版第五章例题内容复现
- 数学建模背景
- 1.学习内容
- 火箭发射升空
- 理论知识
- 2.例题
- 3.问题分析
- 不考虑空气阻力的模型
- 考虑空气阻力的模型
- 4.代码内容复现
- 不考虑空气阻力
- 考虑空气阻力模型
数学建模背景
首先先简单的介绍数学建模是一个怎么样的内容
数学建模是一种将数学方法和技术应用于实际问题解决的过程。它通过建立数学模型来描述、分析和预测现实世界中的各种问题.
数学建模的内容可以包括以下几个方面:
1.问题定义(问题重述):明确问题的目标、约束条件和需求。
2.建立数学模型:根据问题的特点和要求,选择适当的数学方法和技术,建立描述问题的数学模型。
3.模型分析:对建立的数学模型进行分析,推导出模型的性质和特征。
4.模型求解:利用数学工具和计算机技术,求解数学模型以得出问题的解决方案。
5.模型验证和评估:验证模型的有效性和准确性,并评估解决方案的可行性和可行性。
6.结果解释和应用:解释数学模型的结果,提供对问题的洞察力,并将模型的解决方案应用于实际情况。
1.学习内容
所学习的内容的理论基础的描述
简单描述一下本文当中所要使用到的一些数学建模的理论基础的相关知识,重点在于简单了解数学建模相关知识点的应用场景,避免生搬硬套
火箭发射升空
单级小型火箭的发射
考察火箭垂直于地面发射、上升的过程:火箭垂直向上发射后,燃料以一定的速率 燃烧,火焰向后喷射,对火箭产生向前的推力,在克服地球引力和空气阻力的同时,推动 火箭加速飞行.燃料燃尽后火箭依靠获得的速度继续上升,但在引力和阻力的作用下速 度逐渐减小,直到速度等于零,火箭达到最高点.建立数学模型研究火箭上升高度、速度 和加速度的变化规律以及与火箭质量、燃料推力等因素的关系
显然,这个虚拟的场景只是实际发射火箭最初的一个阶段,若不施加其他手段,火箭将从最高点自由下落
火箭发射、上升过程所遵循的基本规律是牛顿第二定律,火箭在运动中受到燃料燃 烧的推力、地球引力和空气阻力的联合作用,其中推力与引力的作用是明确和易于处理的,空气阻力随着火箭速度的增加而变大,但二者之间的数量关系则不易确定.下面先 不考虑空气阻力,建立相对简单的模型,再通过简化、合理的假定将阻力引人模型.
理论知识
本道题当中最重要的就是动力学相关的公式以及积分直接的结合,所以大家只要知道微分方程以及牛顿第二定律
将二阶微分方程化成一阶微分方程组:
{
y
1
′
=
y
2
y
1
(
0
)
=
1
(
初值
)
y
2
′
=
α
y
2
+
β
y
1
+
c
y
2
(
0
)
=
1
(
初值
)
\left\{\begin{matrix} &y^{\prime}_1=y_2 \ & y_1(0)=1(初值) \\ &y^{\prime}_2=\alpha y_2+\beta y_1+c \ & y_2(0)=1(初值) \end{matrix}\right.
{y1′=y2 y2′=αy2+βy1+c y1(0)=1(初值)y2(0)=1(初值)
牛顿第二定律:
F
=
m
a
F=ma
F=ma
2.例题
由于时间的关系,在每一张当中都尽可能地会挑一道两道题进行描述
问题与假设设小型火箭初始质量为 m 0 = 1600 k g m_0=1600kg m0=1600kg,其中包括 m 1 = 1080 k g m_1=1080kg m1=1080kg燃料. 火箭从地面垂直向上发射时,燃料以 r = 18 k g / s r=18kg/s r=18kg/s的速率燃烧,对火箭产生 F = 27000 N F=27000N F=27000N的恒定推力.燃料燃尽后火箭继续上升,直到达到最高点.因为火箭上升高度与地球半 径相比很小,所以可认为整个过程中受到的地球引力不变,重力加速度取 g = 9.8 m / s 2 g=9.8m/s2 g=9.8m/s2。建立火箭上升高度、速度和加速度随时间变化的数学模型,给出燃料燃尽时火箭的高 度、速度和加速度以及火箭到达最高点的时间和高度
3.问题分析
对题目进行简单的分析
不考虑空气阻力的模型
模型建立设火箭t=0时从地面x=0向上发射,火箭高度为
x
(
t
)
x(t)
x(t),速度为
x
˙
(
t
)
\dot{x}(t)
x˙(t) ,加速度为
x
¨
(
t
)
\ddot{x}(t)
x¨(t)。火箭的质量记为
m
(
t
)
m(t)
m(t),随燃料燃烧而减少,有
m
(
t
)
=
m
−
r
t
m(t)=m-rt
m(t)=m−rt。燃料燃尽的 m时间记为
t
1
t_1
t1,显然
t
1
=
−
60
s
t_1=-60s
t1=−60s,t以后火箭质量保持为
m
0
−
m
1
=
520
k
g
m_0-m_1=520kg
m0−m1=520kg。火箭到达最高点的时间记为
t
2
t_2
t2,
t
2
t_2
t2由
v
(
t
2
)
v(t_2)
v(t2)=0确定.
火箭从
x
=
0
x=0
x=0处零初速地发射,上升过程中燃料燃烧阶段受到推力
F
F
F和重力
m
(
t
)
g
m(t)g
m(t)g的作用,按照牛顿第二定律可以写出
(
m
0
−
r
t
)
x
¨
=
F
−
(
m
0
−
r
t
)
g
,
0
≤
t
≤
t
1
,
t
1
=
m
1
r
,
x
(
0
)
=
x
˙
(
0
)
(m_0-rt)\ddot{x}=F-(m_0-rt)g,0≤t≤t1,t1=\frac{m_1}{r},x(0)=\dot{x}(0)
(m0−rt)x¨=F−(m0−rt)g,0≤t≤t1,t1=rm1,x(0)=x˙(0)燃料燃尽后火箭只受重力作用,于是
(
m
0
−
m
1
)
x
¨
=
−
(
m
0
−
m
1
)
g
,
t
1
<
t
⩽
t
2
\left(m_{0}-m_{1}\right) \ddot{x}=-\left(m_{0}-m_{1}\right) g, \quad t_{1}<t \leqslant t_{2}
(m0−m1)x¨=−(m0−m1)g,t1<t⩽t2
接下来就是分情况进行公式的推导以及计算,计算内容如下:

考虑空气阻力的模型
考虑空气阻力的模型将空气阻力与火箭的飞行速度进行了联系,得到了如下表达式
(
m
0
−
r
t
)
x
¨
=
F
−
k
x
˙
2
−
(
m
0
−
r
t
)
g
,
0
⩽
t
⩽
t
1
,
t
1
=
m
1
/
r
,
x
(
0
)
=
x
˙
(
0
)
=
0
(
m
0
−
m
1
)
x
¨
=
−
k
x
˙
2
−
(
m
0
−
m
1
)
g
,
t
1
<
t
⩽
t
2
\begin{array}{c} \left(m_{0}-r t\right) \ddot{x}=F-k \dot{x}^{2}-\left(m_{0}-r t\right) g, 0 \leqslant t \leqslant t_{1}, t_{1}=m_{1} / r, x(0)=\dot{x}(0)=0 \\ \left(m_{0}-m_{1}\right) \ddot{x}=-k \dot{x}^{2}-\left(m_{0}-m_{1}\right) g, t_{1}<t \leqslant t_{2} \end{array}
(m0−rt)x¨=F−kx˙2−(m0−rt)g,0⩽t⩽t1,t1=m1/r,x(0)=x˙(0)=0(m0−m1)x¨=−kx˙2−(m0−m1)g,t1<t⩽t2
将第一个式子改写

以此为基础建立模型,绘制对应图像
4.代码内容复现
时间原因,直接进行代码的书写
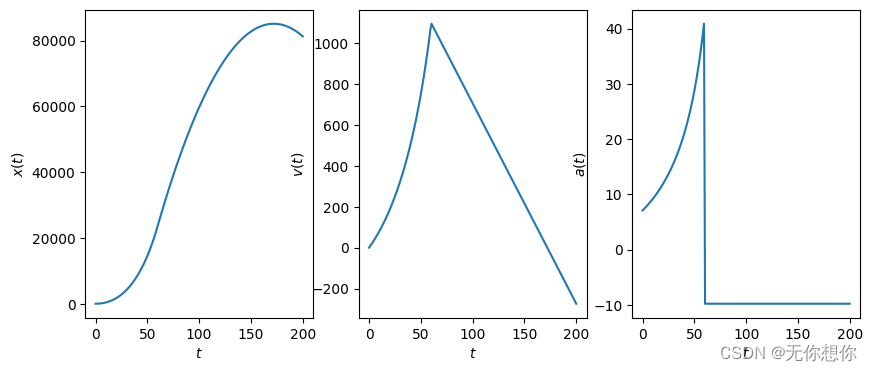
不考虑空气阻力
根据已知的内容计算可得到的具体值,在后续代码的书写当中直接代入
import numpy as np
m0=1600
F=27000
m1=1080
r=18
t1=60.0
g=9.8
v1=-g*60+(F/r)*np.log(m0/(m0-r*60))
x1=-1/2*g*60**2+F*(m0-r*60)*(np.log(m0-r*60)-1)/r**2+((F*np.log(m0))*60)/r-F*m0*(np.log(m0)-1)/r**2
print(v1)
print(x1)
1097.8951449785993
23656.36247839604
#不考虑空气阻力下的方程
from scipy.integrate import odeint
from scipy.integrate import solve_ivp
import numpy as np
import pylab as plt
import math
m0=1600
F=27000
m1=1080
r=18
t1=60.0
g=9.8
t=np.linspace(0,200,200)
v=[]
x=[]
a=[]
for i in range(0,200):
if t[i]<=60:
a=np.hstack([a,-g+F/(m0-r*t[i])])
v=np.hstack([v,-g*t[i]+(F/r)*np.log(m0/(m0-r*t[i]))])
x=np.hstack([x,-1/2*g*t[i]**2+F*(m0-r*t[i])*(np.log(m0-r*t[i])-1)/r**2+((F*np.log(m0))*t[i])/r-F*m0*(np.log(m0)-1)/r**2])
else:
a=np.hstack([a,-g])
v=np.hstack([v,-g*(t[i]-t1)+v1])
x=np.hstack([x,-1/2*g*(t[i]-t1)**2+v1*(t[i]-t1)+x1])
# k=0.3
plt.figure(figsize=(10,4))
plt.subplot(131)
plt.plot(t,x[:])
plt.xlabel('$t$')
plt.ylabel('$x(t)$')
plt.subplot(132)
plt.plot(t,v[:])
plt.xlabel('$t$')
plt.ylabel('$v(t)$')
plt.subplot(133)
plt.plot(t,a[:])
plt.xlabel('$t$')
plt.ylabel('$a(t)$')
plt.show()
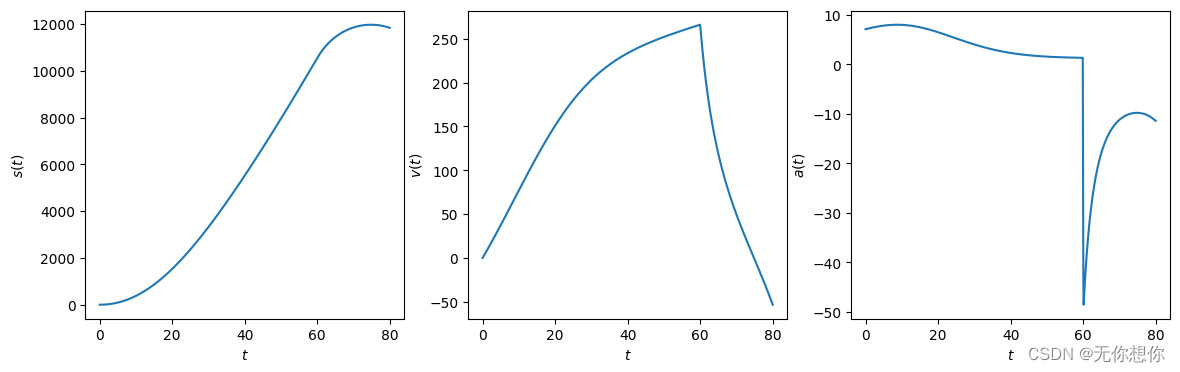
考虑空气阻力模型
使用到的是scipy.integrate当中的odeint进行计算
from scipy.integrate import odeint
from scipy.integrate import solve_ivp
import numpy as np
import pylab as plt
from sympy import symbols,diff
k=0.3
m0=1600
F=27000
m1=1080
r=18
t1=m1/r
g=9.8
def dx(x,t):
x1,x2=x
if t<60:return [x2,-g+(F-k*x2**2)/(m0-r*t)]
elif t>=60:return [x2,-g-(k*x2**2)/(m0-m1)]
# dz=lambda z,t:[z[1],-g+(F-k*z[1]**2)/(m0-r*t)]
t=np.linspace(0,80,1000)
x0=[0,0]
# solve=odeint(dz,[0,0],t)
solve=odeint(dx,x0,t)
# result=solve_ivp(dz,[0,60],[0,0],method='RK45',t_eval=None)
# plt.re('text',usetex=True)
time = np.array(t) # 时间数据
velocity = np.array(solve[:,1]) # 速度数据
# 计算时间间隔
dt = time[1:] - time[:-1]
# 使用中心差分法计算加速度
acceleration = np.zeros_like(velocity)
acceleration[1:-1] = (velocity[2:] - velocity[:-2]) / (2 * dt[1:])
# 处理边界条件
acceleration[0] = (velocity[1] - velocity[0]) / dt[0]
acceleration[-1] = (velocity[-1] - velocity[-2]) / dt[-1]
#print(acceleration)
#print(np.size(acceleration))
plt.figure(figsize=(14,4))
plt.subplot(131)
plt.plot(t,solve[:,0])
plt.xlabel('$t$')
plt.ylabel('$s(t)$')
plt.subplot(132)
plt.plot(t,solve[:,1])
plt.xlabel('$t$')
plt.ylabel('$v(t)$')
plt.subplot(133)
plt.plot(t,acceleration)
plt.xlabel('$t$')
plt.ylabel('$a(t)$')
plt.show()